- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Правильные многогранники, проектная работа ученицы 11 класса
Содержание
- 1. Презентация по теме Правильные многогранники, проектная работа ученицы 11 класса
- 2. выпуклый многогранник называется правильным, если все его
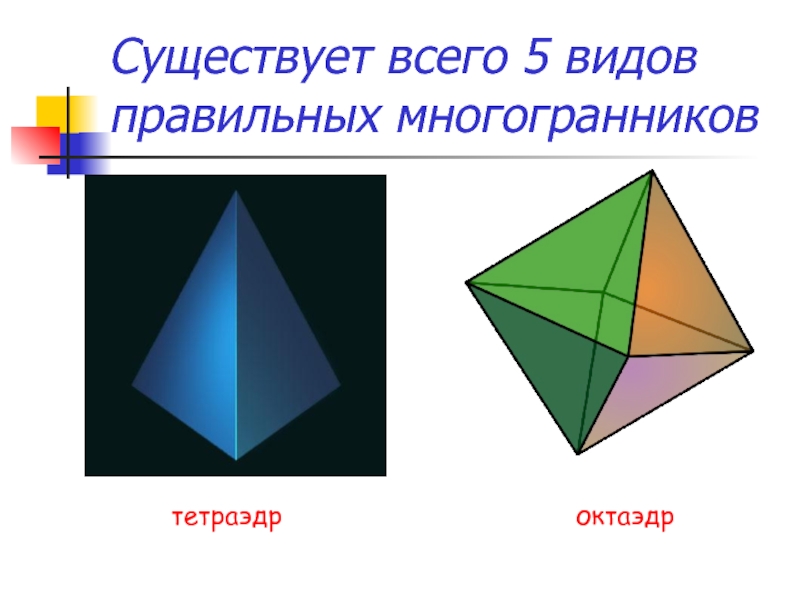
- 3. Существует всего 5 видов правильных многогранниковтетраэдроктаэдр
- 4. икосаэдрдодекаэдргексаэдр
- 5. Слайд 5
- 6. У икосаэдра 30 ребер. Как и у
- 7. Икосаэдр имеет 15 осей симметрии, каждая из
- 8. В природе встречаются объекты, обладающие симметрией 5-го
- 9. Полуправильные многогранники полуправильные многогранники или Архимедовы тела
- 10. В дословном переводе с греческого "тетраэдр",
выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники и, кроме того, в каждой вершине сходится одинаковое число ребер.Правильные многогранники
Слайд 2выпуклый многогранник называется правильным, если все его грани равные правильные многоугольники
и, кроме того, в каждой вершине сходится одинаковое число ребер.
Правильные многогранники
Слайд 5 Икосаэдр
(от греческого ico
– двадцать и hedra – грань)
Правильный выпуклый многогранник, составленный из 20 правильных треугольников. Каждая из 12 вершин икосаэдра является вершиной 5 равносторонних треугольников, поэтому сумма углов при вершине равна 300°.
Правильный выпуклый многогранник, составленный из 20 правильных треугольников. Каждая из 12 вершин икосаэдра является вершиной 5 равносторонних треугольников, поэтому сумма углов при вершине равна 300°.
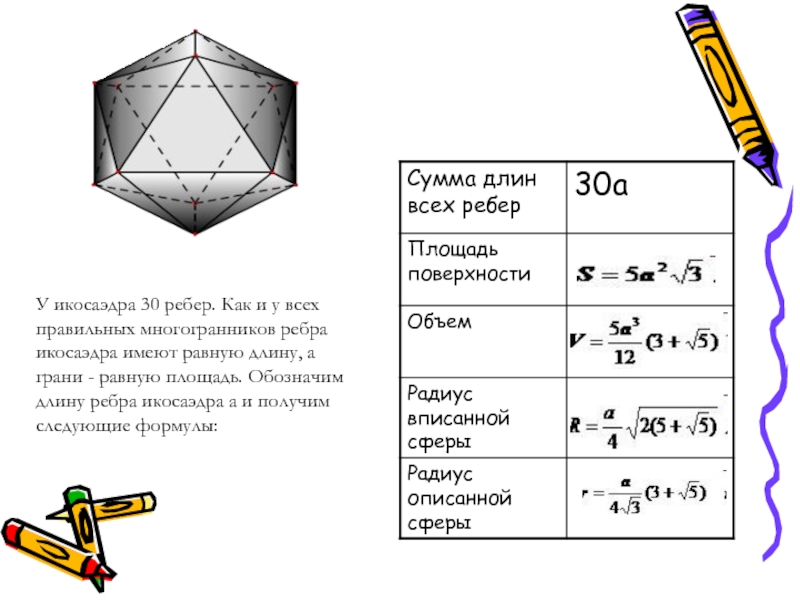
Слайд 6У икосаэдра 30 ребер. Как и у всех правильных многогранников ребра
икосаэдра имеют равную длину, а грани - равную площадь. Обозначим длину ребра икосаэдра а и получим следующие формулы:
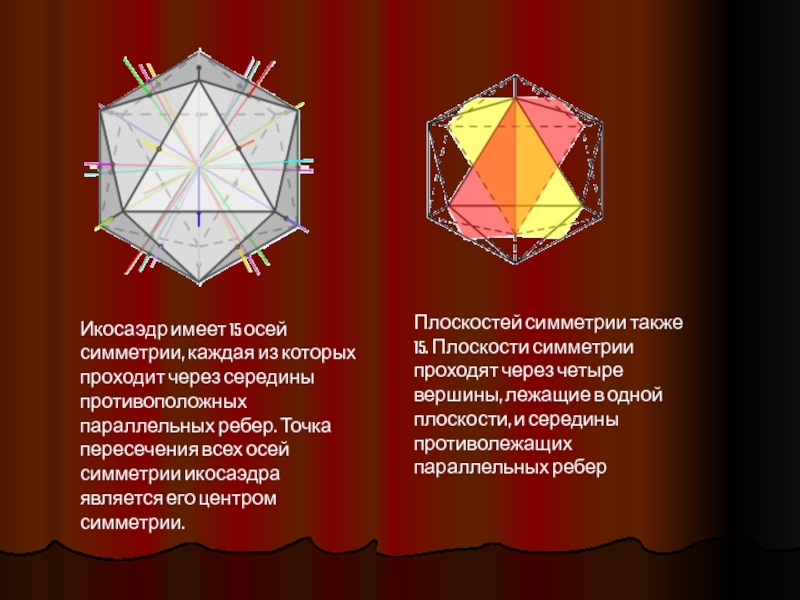
Слайд 7Икосаэдр имеет 15 осей симметрии, каждая из которых проходит через середины
противоположных параллельных ребер. Точка пересечения всех осей симметрии икосаэдра является его центром симметрии.
Плоскостей симметрии также 15. Плоскости симметрии проходят через четыре вершины, лежащие в одной плоскости, и середины противолежащих параллельных ребер
Слайд 8В природе встречаются объекты, обладающие симметрией 5-го порядка. Известны, например, вирусы,
содержащие кластеры в форме икосаэдра. Открытие фуллерена, молекула которого С60 также обладает этим типом симметрии, стимулировало интерес к подобным объектам. Г.Хуберт с сотрудниками (H.Hubert ; Аризонский университет, США) синтезировали кристаллы B6O из смеси B и B2O3, которая выдерживалась при температуре 1700oС и давлении от 4 до 5.5 ГПа в течение 30 мин. Образовавшийся субоксид бора имеет ромбоэдрическую кристаллическую решетку с одним из плоских углов при вершине, равным 63.1o. Это значение очень близко к величине угла 63.4o, необходимого для того, чтобы из 20 тетраэдров можно было составить правильный икосаэдр.
Слайд 9Полуправильные многогранники полуправильные многогранники или Архимедовы тела — выпуклые многогранники, обладающие двумя
свойствами:
Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник);
Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности
Все многогранные углы при вершинах конгруэнтны.
Грани :
8 треугольников
6 восьмиугольников
Вершины :24
Рёбра :36
Конфигурация
вершины :4,6,6
Слайд 10 В дословном переводе с греческого "тетраэдр", "октаэдр", "гексаэдр", "додекаэдр", "икосаэдр"
означают: "четырехгранник", "восьмигранник", "шестигранник". "двенадцатигранник", "двадцатигранник". Этим красивым телам посвящена 13-я книга "Начал" Евклида. Их еще называют телами Платона, т.к. они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или "стихии". Тетраэдр символизировал огонь, т.к. его вершина устремлена вверх; икосаэдр - воду, т.к. он самый "обтекаемый"; куб - землю, как самый "устойчивый"; октаэдр - воздух, как самый "воздушный". Пятый многогранник, додекаэдр, воплощал в себе "все сущее", символизировал все мироздание, считался главным. Гармоничные отношения древние греки считали основой мироздания, поэтому четыре стихии у них были связаны такой пропорцией: земля/вода=воздух/огонь. Атомы "стихий" настраивались Платоном в совершенных консонансах, как четыре струны лиры