- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии в 8 классе по теме: Треугольник. Средняя линия треугольника
Содержание
- 1. Презентация к уроку геометрии в 8 классе по теме: Треугольник. Средняя линия треугольника
- 2. Девиз урока:Обучение без размышления- напрасный труд, мышление без обучения – опасно»
- 3. Дан ∆ АВС, прямая XY параллельна
- 4. СВАМNМN – средняя линия треугольника АВС.Определение: Средней
- 5. Треугольник. Средняя линия треугольника.Тема урока:
- 6. ЦЕЛИ УРОКА: дать определение средней линии треугольника,доказать
- 7. Сколько средних линий имеет треугольник? Задание.Постройте произвольный
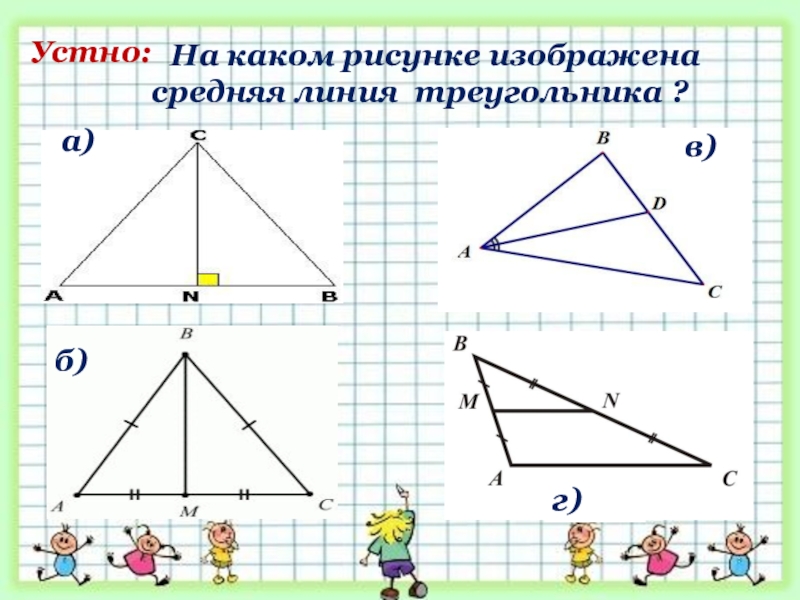
- 8. На каком рисунке изображена средняя линия треугольника ?а)г)б)в)Устно:
- 9. Теорема: Средняя линия треугольника параллельна одной
- 10. 1. Сколько треугольников вы видите?2. Есть ли
- 11. Отрезок MN является средней линией треугольника …в)
- 12. 10 клетокСредняя линия треугольника : 10
- 13. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
- 14. Задача 19 ( ОГЭ 2017)Средняя линия равностороннего
- 15. Слайд 15
- 16. Дорожные знаки
- 17. Слайд 17
- 18. Треугольники в архитектуреВыставочный центр BTEK FlatironBuildingТреугольная башня в Париже Le Project TriangleРусская изба
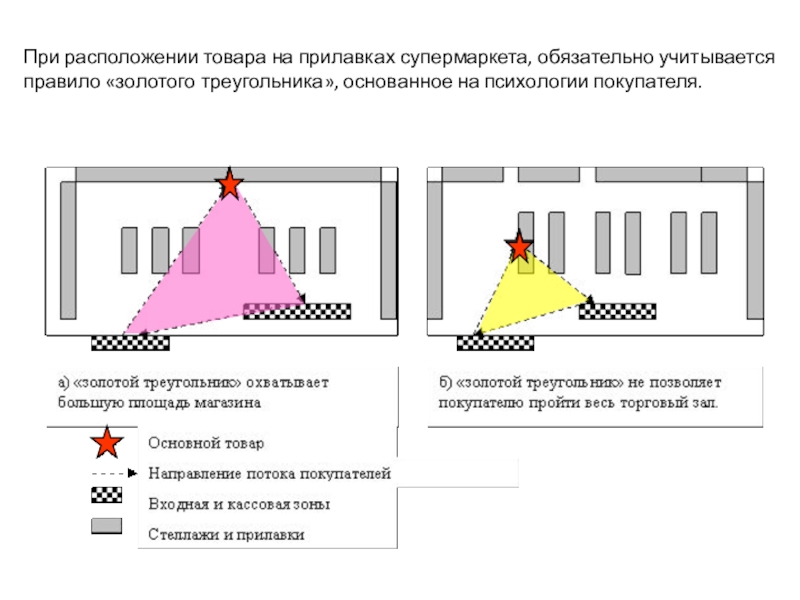
- 19. При расположении товара на прилавках супермаркета, обязательно учитывается правило «золотого треугольника», основанное на психологии покупателя.
- 20. Каменный
- 21. Какие новые знания получены на уроке?Что называют средней линией треугольника?Сформулируйте теорему о средней линии треугольника.Подведем итог
- 22. Моё настроение Отличное!Все понятно!Непонятное!Есть над чем подумать…
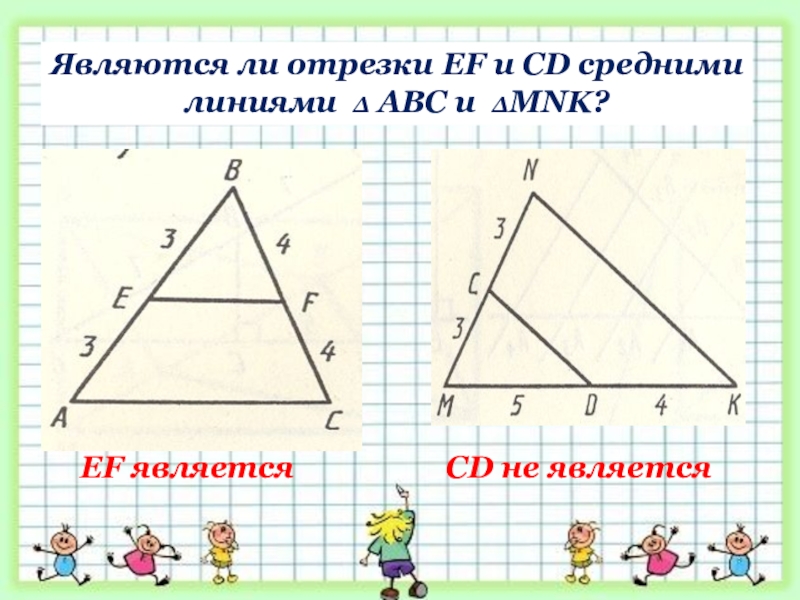
- 23. Являются ли отрезки EF и CD средними линиями ∆ АВС и ∆MNK?EF являетсяCD не является
- 24. ABCMДано: S∆ABC = 40 см²Найти: SΔMNK KN
- 25. Найти
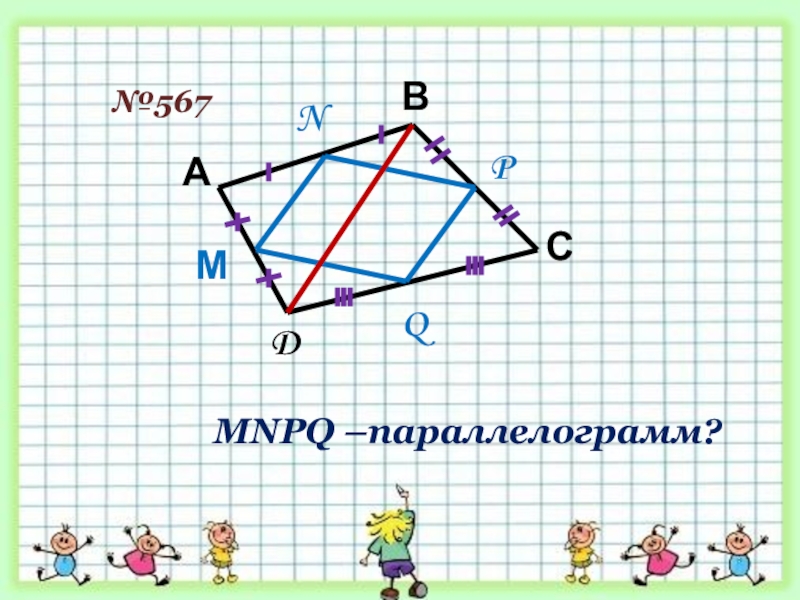
- 26. №567АВСDМNPQMNPQ –параллелограмм?
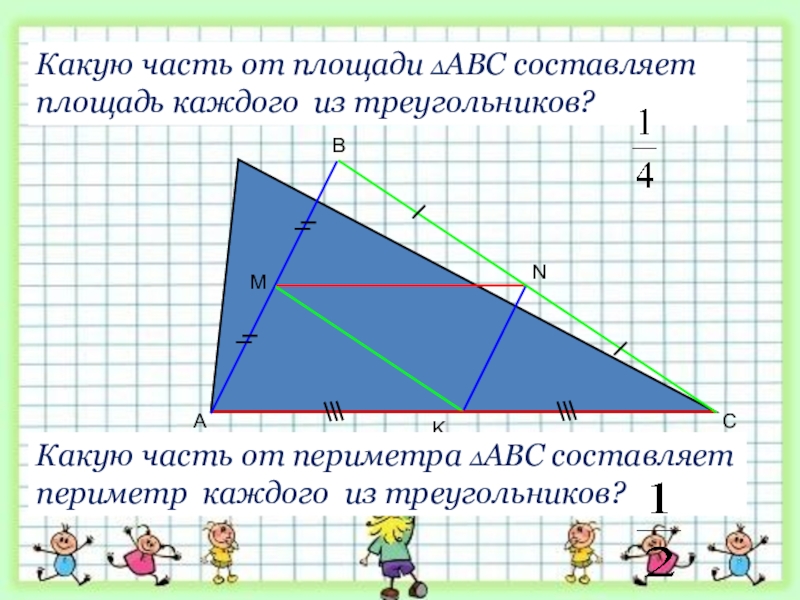
- 27. ABCMKNКакую часть от площади ∆АВС составляет площадь
- 28. 2) Задача3,5ABCNM3 4 Дано: MN
- 29. Спасибо за внимание!!!
- 30. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.
- 31. ЦЕЛИ УРОКА: Дать определение средней линии треугольника.Доказать
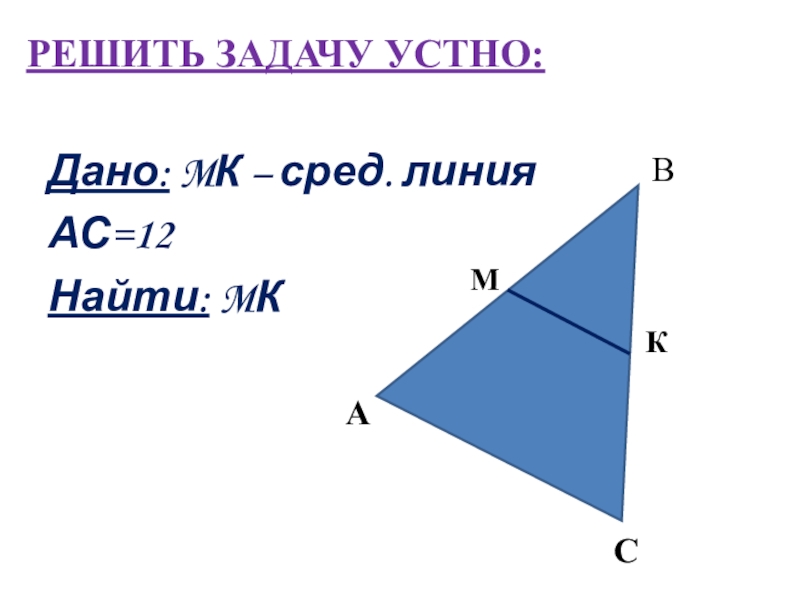
- 32. РЕШИТЬ ЗАДАЧУ УСТНО:Дано: MК – сред. линияАС=12Найти: MК АКМСВ
- 33. Теорема Средняя линия треугольника параллельна одной
Слайд 4
С
В
А
М
N
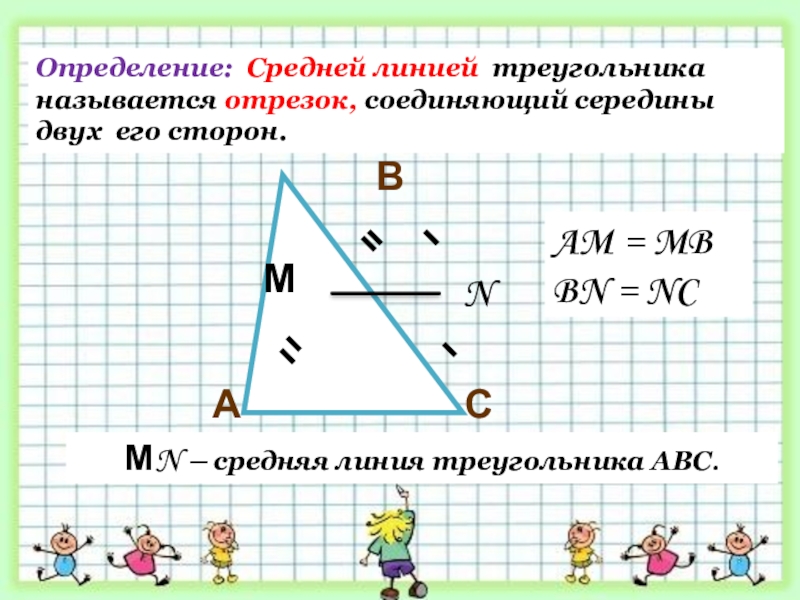
МN – средняя линия треугольника АВС.
Определение: Средней линией треугольника называется отрезок,
AM = MB
BN = NC
Слайд 6ЦЕЛИ УРОКА:
дать определение средней линии треугольника,
доказать теорему о средней линии треугольника,
решать
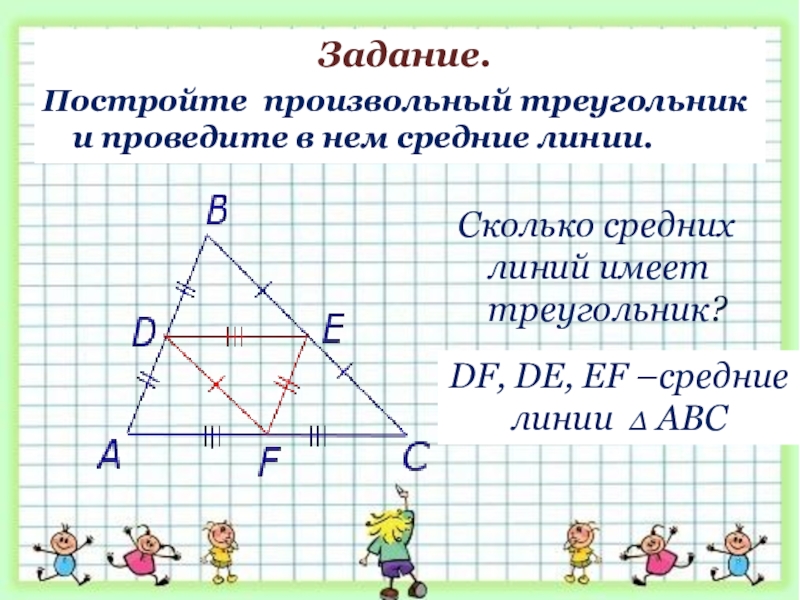
Слайд 7Сколько средних линий имеет треугольник?
Задание.
Постройте произвольный треугольник и проведите в
DF, DE, EF –средние линии ∆ АВС
Слайд 9Теорема: Средняя линия треугольника параллельна одной из его сторон и
С
В
А
М
N
Дано: ΔАВС, МN – средняя линия.
Доказать: МN || АС, МN =½ АС
Доказательство:
ΔАВС ~ ΔВМN,
т.к. ВМ:ВА = ВN:ВС=1:2 и угол В – общий.
2. Угол ВМN равен углу ВАС,
а они соответственные при прямых МN и АС и секущей АВ. Значит, МN || АС.
3. Т.к. ВМ:ВА =1:2, то и МN:АС=1:2.
Слайд 10
1. Сколько треугольников вы видите?
2. Есть ли равные треугольники? Почему?
Устно:
3. Сколько
∆ADF, ∆ DBE, ∆ ECF, ∆ DEF, ∆ ABC
∆ADF= ∆ DBE= ∆ ECF= ∆ DEF
ADEF, DBEF, ECFD
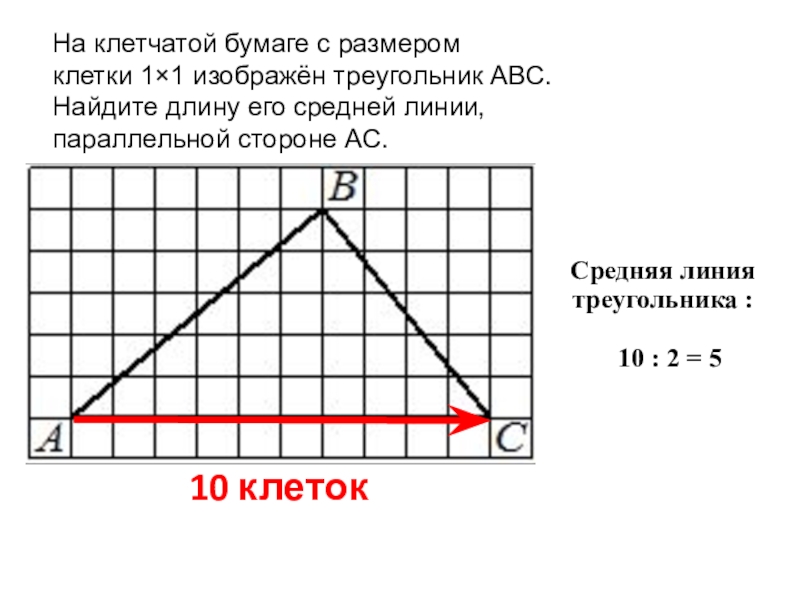
Слайд 12 10 клеток
Средняя линия треугольника :
10 : 2 = 5
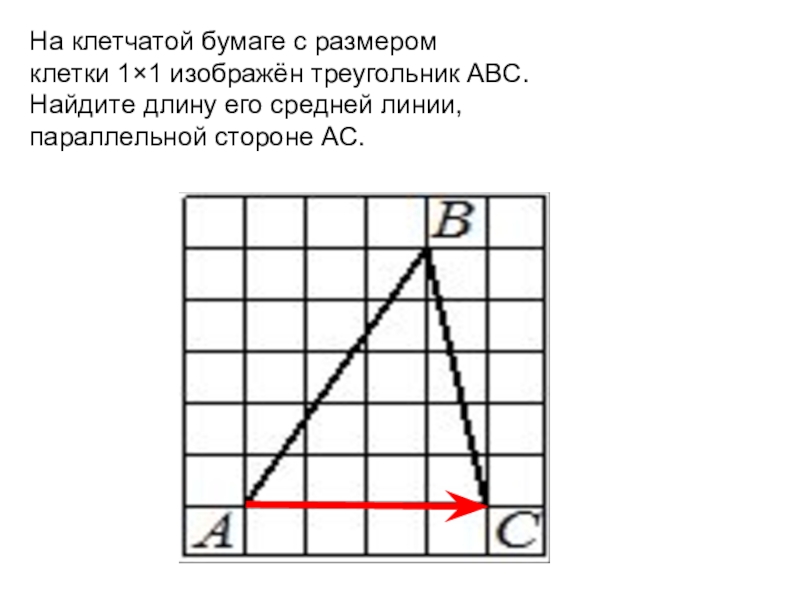
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC.
Найдите длину его средней линии,
параллельной стороне AC.
Слайд 13На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней
Слайд 14Задача 19 ( ОГЭ 2017)
Средняя линия равностороннего треугольника АВС равна 8
А
В
С
Р ∆ АВС = 48 см
Слайд 18Треугольники в архитектуре
Выставочный
центр BTEK
FlatironBuilding
Треугольная башня
в Париже Le Project
Русская изба
Слайд 19При расположении товара на прилавках супермаркета, обязательно учитывается правило «золотого треугольника»,
Слайд 21Какие новые знания получены на уроке?
Что называют средней линией треугольника?
Сформулируйте теорему
Подведем итог
Слайд 25
Найти площадь треугольника, если высота,
Задача 3 ( ГИА 2013)
Н
SΔ АВС =50 см²
Слайд 27
A
B
C
M
K
N
Какую часть от площади ∆АВС составляет площадь каждого из треугольников?
Какую часть
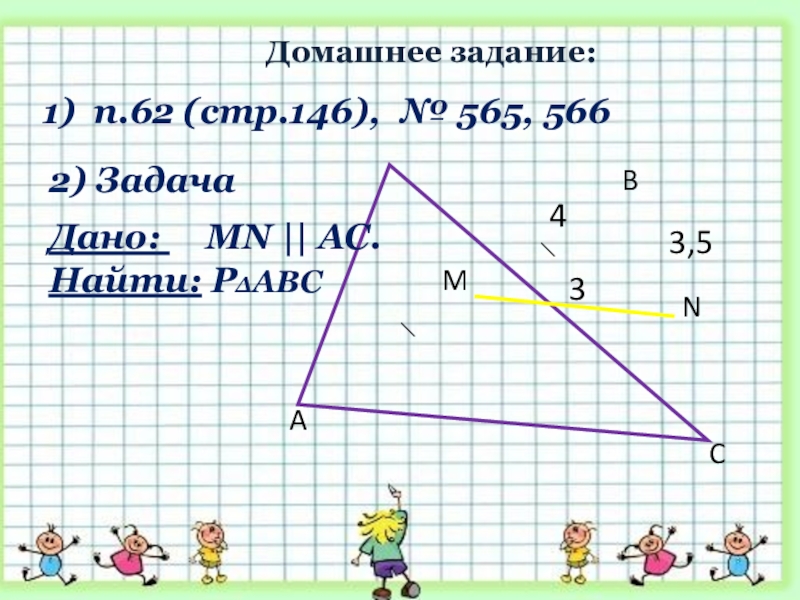
Слайд 282) Задача
3,5
A
B
C
N
M
3
4
Дано: MN || AC.
Найти: Р∆АВС
1) п.62 (стр.146), № 565, 566
Домашнее задание:
Слайд 30На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней
Слайд 31ЦЕЛИ УРОКА:
Дать определение средней линии треугольника.
Доказать теорему о средней линии треугольника.
Решать
средней линии.
Слайд 33
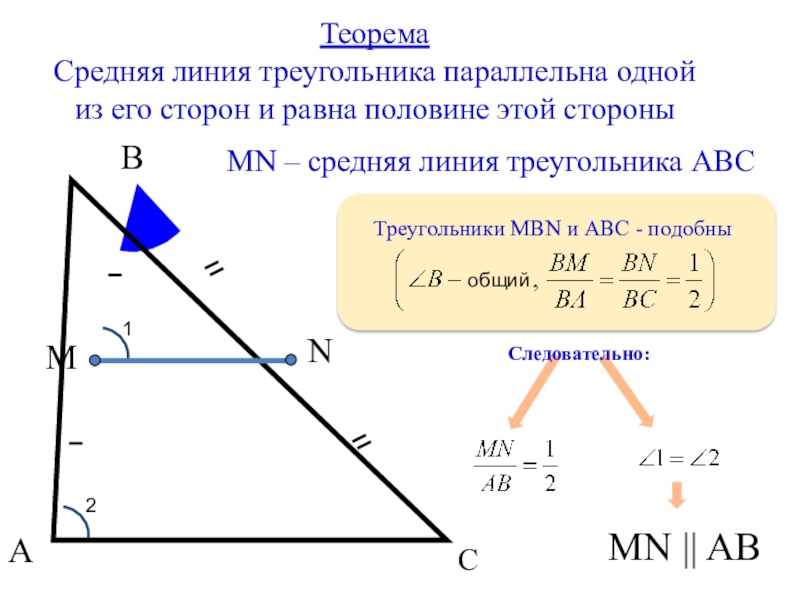
Теорема
Средняя линия треугольника параллельна одной из его сторон и равна
А
В
С
М
N
MN – средняя линия треугольника АВС
Треугольники MBN и АВС - подобны
Следовательно:
MN || AB
1
2