районы Илексаз төп гомум белем бирү мәктәбенең
VIII сыйныф укучысы Шәвәлиева Айгөлнең фәнни-эзләнү эше.
Җитәкчесе: Сарман районы Илексаз төп гомум белем бирү мәктәбенең математика укытучысы Шәвәлиев Вахит Вагыйз улы
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Эзләнүгә таяныч -Каюм Насыйри мирасы безгә табыш
Содержание
- 1. Презентация по математике Эзләнүгә таяныч -Каюм Насыйри мирасы безгә табыш
- 2. КАЮМ НАСЫЙРИНЫҢ ГЕОМЕТРИЯДӘ РОЛЕ
- 3. ФАРАЗ Мине
- 4. Эпиграф
- 5. ПланI. Каюм Насыйри – күренекле математик-галим.II. К.
- 6. Каюм Насыйри – күренекле
- 7. К. Насыйриның “Истыйляхәт гыйльме һәндәсе” (“Геометрия фәне
- 8. Елганың киңлеген үлчәү Каюм бабай мәсьәләсе
- 9. Тау биеклеген үлчәү Каюм бабай мәсьәләсе Тауның
- 10. Күлнең киңлеген үлчәү Каюм бабай мәсьәләсе
- 11. Манара биеклеген үлчәү Каюм бабай мәсьәләсеЯнына
- 12. Илексаз мәктәбе эчендәге икенче этажга менү баскы-
- 13. Илексаз авылындагы күлнең киңлеген үлчәү .
- 14. Иләк елгасының киңлеген үлчәүКаюм Насыйри ысулыннан файдаланып,
- 15. Илексаз авылындагы күлнең
- 16. Илексаз авылының мәчет манарасы биеклеген үлчәү
- 17. Илексаз авылының мәчет манарасы биеклеген үлчәү
- 18. Нәтиҗә Бу эшләрне үтәү барышында мин
- 19. Кулланылган әдәбият1. Геометрия, 7- 9 нчы сыйныфлар
КАЮМ НАСЫЙРИНЫҢ ГЕОМЕТРИЯДӘ РОЛЕ Максат: 1.Геометрия фәне буенча белемнәрне киңәйтү;2.Каюм Насыйриның математика хезмәтләрен өйрәнү;3.Үз җирлегебездәге үлчәмнәр белән геометрик мәсьәләләрне чишүне Каюм Насыйри тарафыннан тәкъдим ителгән ысуллар ярдәмендә эшләүнең
Слайд 2 КАЮМ НАСЫЙРИНЫҢ ГЕОМЕТРИЯДӘ РОЛЕ
Максат:
1.Геометрия фәне буенча белемнәрне киңәйтү;
2.Каюм Насыйриның математика хезмәтләрен өйрәнү;
3.Үз җирлегебездәге үлчәмнәр белән геометрик мәсьәләләрне чишүне Каюм Насыйри тарафыннан тәкъдим ителгән ысуллар ярдәмендә эшләүнең актуальлеген күрсәтү.
Бурычлар:
Каюм Насыйриның геометрия буенча алган белемнәрен тирәнәйтү;
математик фикерләүне үстерү.
1.Геометрия фәне буенча белемнәрне киңәйтү;
2.Каюм Насыйриның математика хезмәтләрен өйрәнү;
3.Үз җирлегебездәге үлчәмнәр белән геометрик мәсьәләләрне чишүне Каюм Насыйри тарафыннан тәкъдим ителгән ысуллар ярдәмендә эшләүнең актуальлеген күрсәтү.
Бурычлар:
Каюм Насыйриның геометрия буенча алган белемнәрен тирәнәйтү;
математик фикерләүне үстерү.
Эзләнү ысуллары:
-мәгълүмат туплау;
-мәгълүматны эшкәртү;
-үз җирлегебездә үлчәү эшләре алып бару.
Эзләнү объекты:
Каюм Насыйриның математик хезмәтләре
Слайд 3 ФАРАЗ
Мине Каюм Насыйриның математик хезмәтләре
кызыксындырды. Аның “Истыйляхәт гыйльме һәндәсе” (“Геометрия фәне терминнары”) дигән китабында геометрик мәгълүматларның көнкүрештә, көндәлек тормышта кайларда кулланылуы шактый тулы күрсәтелгән. Мәчет манаралары, биналар, агачлар һәм тауларның биеклеген, елга һәм күлләрнең киңлеген, шулай ук ике предмет арасындагы ераклыкны табу кагыйдәләре бирелгән. Эзләнү эшемдә мин Каюм Насыйри тарафыннан эшләнгән ысулларның актуальлеген,ягъни практикада киң кулланыш табуын күрсәтергә телим.
Слайд 4Эпиграф
Иҗатының нинди тармагы юк:
Җәгърәфия дисәң... тәрбия,
Татарның ул – Ломоносовы , дип,
Чит милләтләр хәтта баш ия!
Эльмира Шәрифуллина
Татарның ул – Ломоносовы , дип,
Чит милләтләр хәтта баш ия!
Эльмира Шәрифуллина
Слайд 5План
I. Каюм Насыйри – күренекле математик-галим.
II. К. Насыйриның “Истыйляхәт гыйльме һәндәсе”
(“Геометрия фәне терминнары”) китабы.
1. Татарча математик терминнарның янәшә кулланылуы.
2. Геометрик мәгълүматларның көнкүрештә, көндәлек тормыш шартларында кулланылуы.
3.Илексаз авылының объектларында үлчәү эшләре үткәрү.
III. К. Насыйриның математика фәне үсешендәге эшчәнлеге.
Кулланылган әдәбият.
1. Татарча математик терминнарның янәшә кулланылуы.
2. Геометрик мәгълүматларның көнкүрештә, көндәлек тормыш шартларында кулланылуы.
3.Илексаз авылының объектларында үлчәү эшләре үткәрү.
III. К. Насыйриның математика фәне үсешендәге эшчәнлеге.
Кулланылган әдәбият.
Слайд 6 Каюм Насыйри – күренекле
математик-галим
Татар мәгърифәтчесе
Каюм Насыйри үз вакытында халыкка күпьяклы белем бирергә тырышкан, татар телендә арифметикадан беренче “Хисаплык”китабы язган , методик ярдәмлекләр төзегән.Беренчеләрдән булып, Европа илләрендә кабул ителгән гарәп цифрлары кулланган.Фәнни терминнарда халыкка аңлашылмаган гарәп,фарсы сүзләрен татар сүзләре белән алмаштырган.
Слайд 7К. Насыйриның “Истыйляхәт гыйльме һәндәсе” (“Геометрия фәне терминнары”) китабы
1895 елда Казан
Император университеты типографиясендә К.Насыйриның “Истыйляхәт гыйльме һәндәсе” (“Геометрия фәне терминнары”) дигән китабы дөнья күрә.Анда гарәпчә һәм татарча терминнар янәшә кулланыла
Слайд 8Елганың киңлеген үлчәү
Каюм бабай мәсьәләсе
В ноктасына туктап, елганың аргы
ягында бер агачны А дип билгеләп,елга аркылы шул агачка туры сызык фараз кыйлдык һәм бу урынымызга билге өчен бер казык кагып куйдык. Аннан “... мәсәлән, бер кечерәк елганың киңлеген үлчәмәк булдык.(Рәс. 1) В ноктасында туктап, елганың аргы ягында бер агачны (А) билгеләп, елга соң елга буйлап түбән таба 25 сажинлап җирне барып, Е ноктасына туктадык. Баягы агачка таба янә бер туры сызык фараз кыйлдык. Бу торган җиребезгә янә бер казык кактык. Аннан соң В дан Е га чаклы үлчәдек – 25 сажин булды. 25 нең биштән бере биш сажиндыр. Е ноктасыннан С ноктасына туры сызык тартып, анда бер казык утырттык. Янә елганың аргы ягындагы агачтан килә дип уйланылган сызыкны Е ноктасы аша уздырып, ниһаять, К ноктасына бер казык кактык. Аннан К казыгыннан С казыгына бер туры тартып үлчәдек, ике сажин ярым булды. Аны бишкә тапкырладык – унике ярым хасил булды. Бәс, елганың киңлеге унике ярымдыр”.
Слайд 9Тау биеклеген үлчәү
Каюм бабай мәсьәләсе
Тауның биеклеген белү өчен тау итәгенең
А ноктасында вертикаль казык кагыла. Аның икенче очы белән тау итәгенә орынырлык итеп горизонталь таяк куела. Казыкның биеклеге Һ1 үлчәп алына. Кабат казык кадала һәм, беренче очрактагы кебек, аңа горизонталь таяк салына. Һ2 биеклеге үлчәп алына.Тау түбәсендәге М ноктасына җиткәнче үлчәү шулай дәвам итә. Бар үлчәү нәтиҗәләре суммасы (безнең очракта 4 тапкыр) тулаем тауның биеклегенә Н=Һ1+Һ2+Һ3+Һ4 тигез була.
Слайд 10Күлнең киңлеген үлчәү
Каюм бабай мәсьәләсе
Әгәр дә ике
әйбер арасындагы мәсафәтне белмәк өчен үлчәгәндә аркан белән вә колач белән үлчәргә мөмкин түгел икән, аны ошбу ысул белән үлчәрмез. Мәсәлән, А белән В арасында манигь (киртә, комачау) булучы күл яки саз булсын. Әүвәл А һәм В нокталарында казык кагарбыз. Аннан бер тарафка таба байтаграк җиргә китеп, бер урынны, мәсәлән, О ноктасын табарбыз ки, анда А һәм В нокталары аерым-ачык күренер. Аннан соң АОК һәм ВОК турылары уздырабыз. АО ны үлчибез һәм О ноктасыннан АК турысына ОЕ = ОА кисемтәләрен, ВМ турысында да О ноктасыннан ОС = ОВ кисемтәләрен салабыз. АОВ = СОЕ (ике ягы һәм алар арасындагы почмагы буенча) өчпочмаклары килеп чыгар. Аннары үлчәгеч бау белән СЕ арасын үлчибез, бу ара күл киңлегенә ,ягъни АВ арасына тәңгәл булыр.
Слайд 11Манара биеклеген үлчәү
Каюм бабай мәсьәләсе
Янына барып үлчәргә мөмкин бер гыймарәтнең
(бинаның) яки бер тауның яки бер манараның биеклеген белмәк өчен ансат бер ысулы бардыр. (Рәсем 3) Мәсәлән, мәчет манарасының биеклеге ничә аршин яки ничә колач икәнлеген белү өчен мәчет нигезеннән бераз арырак В ноктасында бер казык утыртыла. Казык башының Е ноктасында мәчет манарасының иң югары М нокасына юнәлгән визир беркетелә.
Визирның икенче ягына чыгып, визир сызыгы юнәлеше буенча җир өстендә A’ ноктасын билгелибез. Ике охшаш АA’М һәм ВA’Е өчпочмаклары барлыкка килде. АA’ һәм ВA’ арасын, ВЕ казыгы озынлыгын үлчәгәч, эзләнелә торган манара биеклеген – АМ ны пропорция төзеп табарга була.
Визирның икенче ягына чыгып, визир сызыгы юнәлеше буенча җир өстендә A’ ноктасын билгелибез. Ике охшаш АA’М һәм ВA’Е өчпочмаклары барлыкка килде. АA’ һәм ВA’ арасын, ВЕ казыгы озынлыгын үлчәгәч, эзләнелә торган манара биеклеген – АМ ны пропорция төзеп табарга була.
Слайд 12Илексаз мәктәбе эчендәге икенче этажга менү баскы- чының биеклеген үлчәү
Бу практик эш Каюм Насыйринең тау биеклеген үлчәү мәсьәләсенә бик охшаш.Баскыч басмалары n=12 данә,һәр басма биеклеге һ=13 см. Димәк,баскыч биеклеге Н1= n*һ= =12*13 =156 см.Ә ике кат арасы, рәсемнән күренгәнчә, ике баскычтан тора. Шунлыктан, бер араны 2гә тапкырлыйсы гына кала : Н = 2*Н1 =2*156 см =312 см =3 м 12 см.
Җавап : ике этаж арасындагы баскыч биеклеге 3 м 12 см.
Җавап : ике этаж арасындагы баскыч биеклеге 3 м 12 см.
Слайд 14Иләк елгасының киңлеген үлчәү
Каюм Насыйри ысулыннан файдаланып, Илексаз авылындагы Иләк елгасының
киңлеген үлчәдек.
В ноктасында туктап, Иләк елгасының аргы ягында елга ярына АВ турысы перпендикуляр булырдай А ноктасын билгеләдек (берәр агач). Елга аркылы В дан шул А ноктасына күңелдән туры сызык үткәрәбез. Аннан соң Иләк елгасы яры буйлап түбән таба Е ноктасын билгеләдек һәм рулетка ярдәмендә ВЕ арасын үлчәдек , ВЕ=12 метр булды. ВЕ турысын дәвам итеп , ЕСК өчпочмагының яклары аңа охшаш АВЕ өчпочмагы якларыннан 5 мәртәбә кечерәк булырлык итеп , ягъни ЕС=12:5=2,4 метр ара үлчәп, С ноктасына бер казык утырттык. Янә елганың аргы ягындагы А ноктасыннан килә дип уйланылган сызыкны Е ноктасы аша уздырып , К ноктасын билгеләдек. СК ┴ ВЕ булырга тиеш. Аннары соң С ноктасыннан К ноктасына кадәр бер туры тартып,СК кисемтәсен үлчәдек, СК=1 метр 40 сантиметр булды. Аны бишкә тапкырладык: 1,4 м *5=7 метр булды.
Димәк, Иләк елгасының киңлеге без үлчәгән урында 7 метр.
В ноктасында туктап, Иләк елгасының аргы ягында елга ярына АВ турысы перпендикуляр булырдай А ноктасын билгеләдек (берәр агач). Елга аркылы В дан шул А ноктасына күңелдән туры сызык үткәрәбез. Аннан соң Иләк елгасы яры буйлап түбән таба Е ноктасын билгеләдек һәм рулетка ярдәмендә ВЕ арасын үлчәдек , ВЕ=12 метр булды. ВЕ турысын дәвам итеп , ЕСК өчпочмагының яклары аңа охшаш АВЕ өчпочмагы якларыннан 5 мәртәбә кечерәк булырлык итеп , ягъни ЕС=12:5=2,4 метр ара үлчәп, С ноктасына бер казык утырттык. Янә елганың аргы ягындагы А ноктасыннан килә дип уйланылган сызыкны Е ноктасы аша уздырып , К ноктасын билгеләдек. СК ┴ ВЕ булырга тиеш. Аннары соң С ноктасыннан К ноктасына кадәр бер туры тартып,СК кисемтәсен үлчәдек, СК=1 метр 40 сантиметр булды. Аны бишкә тапкырладык: 1,4 м *5=7 метр булды.
Димәк, Иләк елгасының киңлеге без үлчәгән урында 7 метр.
Слайд 15Илексаз авылындагы күлнең киңлеген үлчәү
Илексаз авылындагы күлнең киңлеген үлчәү өчен А һәм В нокталарын казык белән билгеләдек. Аннан соң күлдән ераклашып, казык белән О ноктасын билгеләдек, бу урында А һәм В нокталары аерым –ачык күренә. Аннан соң АО ның дәвамында АК һәм ВО ның дәвамында ВМ турыларын уздырдык, М һәм К нокталарында казыкларны билгеләдек. АО ны үлчәдек һәм О ноктасыннан АК турысында ОЕ=АО =17м кисемтәләрен , ВМ турысында О ноктасыннан ОС=ОВ=24м кисемталәрен салдык. АОВ һәм СОЕ өчпочмаклары өчпочмаклар тигезлегенең беренче билгесе буенча тигез булгач, рулетка белән СЕ арасын үлчәдек. СЕ=36м булды, димәк,АВ= СЕ =36 метр.
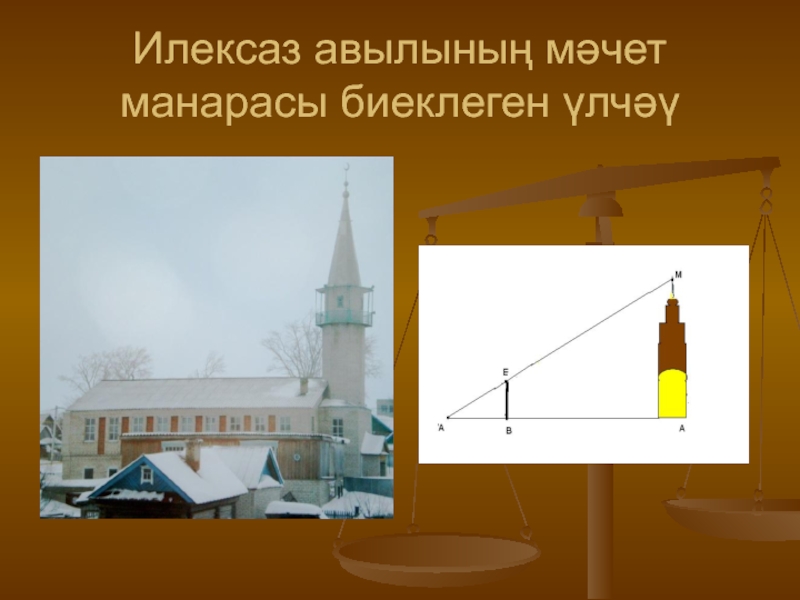
Слайд 17Илексаз авылының мәчет манарасы биеклеген үлчәү
Моның өчен әйләнә
торган планкасы булган ЕВ колгасын мәчет нигезеннән билгеле бер ераклыкта кадап куябыз да планканы мәчетнең югарыгы М ноктасына юнәлтәбез. Җир өстендә МЕ турысының җир өслеге белән кисешү ноктасы С ны билгелибез. ВA’=1,5 м ВЕ=1,6 м, АA’=22,5 м булса,
24 м
Слайд 18Нәтиҗә
Бу эшләрне үтәү барышында мин геометрия фәненнән белемнәремне тирәнәйттем,
Каюм Насыйриның геометрия буенча хезмәтләрен өйрәндем һәм фәнни юнәлештә эзләнеп,аны практикада кулландым.
Слайд 19Кулланылган әдәбият
1. Геометрия, 7- 9 нчы сыйныфлар өчен дәреслек, Казан, “Мәгариф”
, Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев һ. б. Казан, “Мәгариф”,2011,21-нче басма,28-43,138-155 битләр.
2. В. Беркутов “Каюм Насыйри һәм математика” , “Мәгариф” , 2008 ел, №7,60-61 битләр.
3. Ә.Н.Хуҗиәхмәтов “Мәгърифәт йолдызлыгы”. Казан, “Мәгариф” нәшрияты, 2002 ел,169 -199 битләр.
4. Ә.Н.Хуҗиәхмәтов “Мәгърифәт мәңгелек юлдаш”. Казан, “ТаРИХ” нәшрияты, 2002 ел.
2. В. Беркутов “Каюм Насыйри һәм математика” , “Мәгариф” , 2008 ел, №7,60-61 битләр.
3. Ә.Н.Хуҗиәхмәтов “Мәгърифәт йолдызлыгы”. Казан, “Мәгариф” нәшрияты, 2002 ел,169 -199 битләр.
4. Ә.Н.Хуҗиәхмәтов “Мәгърифәт мәңгелек юлдаш”. Казан, “ТаРИХ” нәшрияты, 2002 ел.