- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Вневписанные окружности треугольника
Содержание
- 1. Презентация по геометрии Вневписанные окружности треугольника
- 2. Задача ЕГЭ 2011 Прямая, перпендикулярная гипотенузе прямоугольного
- 3. Для решения данного типа задач необходимо знать определение и некоторые свойства вневписанной окружности.
- 4. Вневписанная окружность треугольника —окружность, касающаяся одной из сторон треугольника
- 5. Свойство 1. Радиус вневписанной окружности, касающейся стороны
- 6. Решение.Пусть К – т. пересечения биссектрис ∠MBC
- 7. Свойство 2.Расстояния от вершины угла треугольника до
- 8. Свойство 3.Радиус вневписанной окружности, касающейся сторон
- 9. Свойство 4. Площадь треугольника можно вычислить
- 10. Некоторые свойства вневписанной окружности прямоугольного треугольникаСвойство 1.
- 11. Свойство 5. Расстояния между центрами вневписанных окружностей
- 12. Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от
- 13. 2-й случай1)Прямоугольные треугольники AMN и АВС подобны,
- 14. Задача 2 Решение.Точка E равноудалена от прямых
- 15. Знание некоторых свойств вневписанной окружности быстро приводит
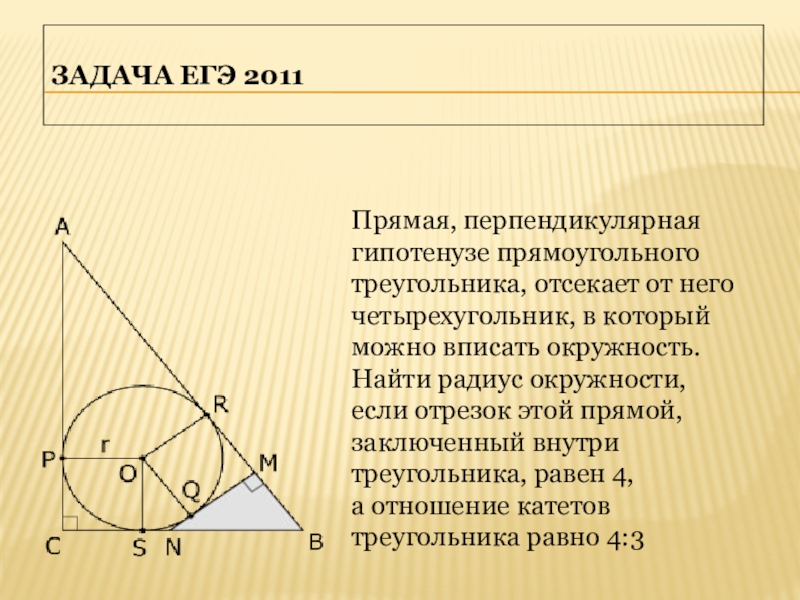
Слайд 2Задача ЕГЭ 2011
Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него
Слайд 3 Для решения данного типа задач необходимо знать определение и некоторые свойства
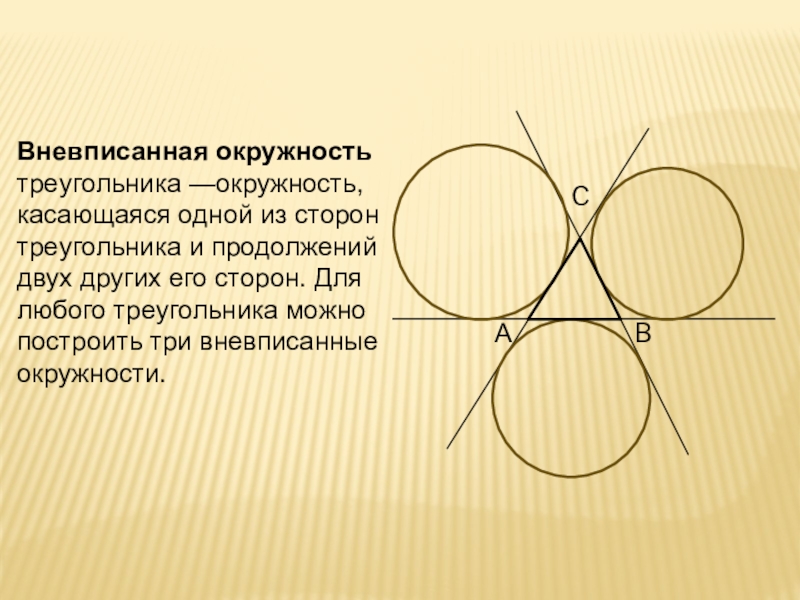
Слайд 4Вневписанная окружность треугольника —окружность, касающаяся одной из сторон треугольника и продолжений двух других
Слайд 5
Свойство 1.
Радиус вневписанной окружности, касающейся стороны треугольника, имеющей длину a,
где S, p – площадь и полупериметр рассматриваемого треугольника.
Некоторые свойства вневписанной окружности
Слайд 6Решение.
Пусть К – т. пересечения биссектрис ∠MBC и ∠BCN.
Т.
2.
3.
4.
5.
Следствие.
Центр вневписанной окружности треугольника есть точка пересечения биссектрисы внутреннего угла, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника.
a
Слайд 7Свойство 2.
Расстояния от вершины угла треугольника до точек касания
вневписанной окружности со
полупериметру данного треугольника.
AM = AN = p
Слайд 8 Свойство 3.
Радиус вневписанной окружности, касающейся сторон внутреннего угла данного треугольника,
треугольника на тангенс половины этого угла, т.е.
Слайд 9 Свойство 4.
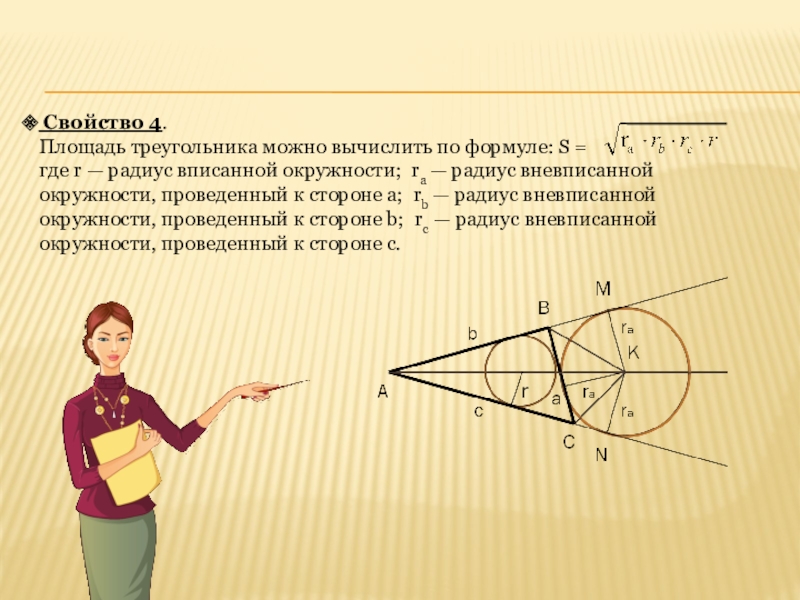
Площадь треугольника можно вычислить по формуле: S =
где r — радиус вписанной окружности; ra — радиус вневписанной окружности, проведенный к стороне a; rb — радиус вневписанной окружности, проведенный к стороне b; rc — радиус вневписанной окружности, проведенный к стороне c.
r
Слайд 10Некоторые свойства вневписанной окружности прямоугольного треугольника
Свойство 1. Радиус вневписанной окружности, касающейся
Свойство 2. Катет прямоугольного треугольника равен сумме радиусов окружностей вписанной и вневписанной, касающейся этого катета, то есть a = ra+ r и b = rb + r.
Свойство 3. Катеты прямоугольного треугольника АВС с прямым углом в вершине С могут быть найдены через радиусы ra, rb, rc вневписанных окружностей по формулам:
Слайд 11Свойство 5. Расстояния между центрами вневписанных окружностей треугольника ABC с прямым
Свойство 4. Площадь прямоугольного треугольника АВС с прямым углом в вершине С может быть найдена через радиус r вписанной и радиусы ra, rb, rc вневписанных окружностей по одной из формул:
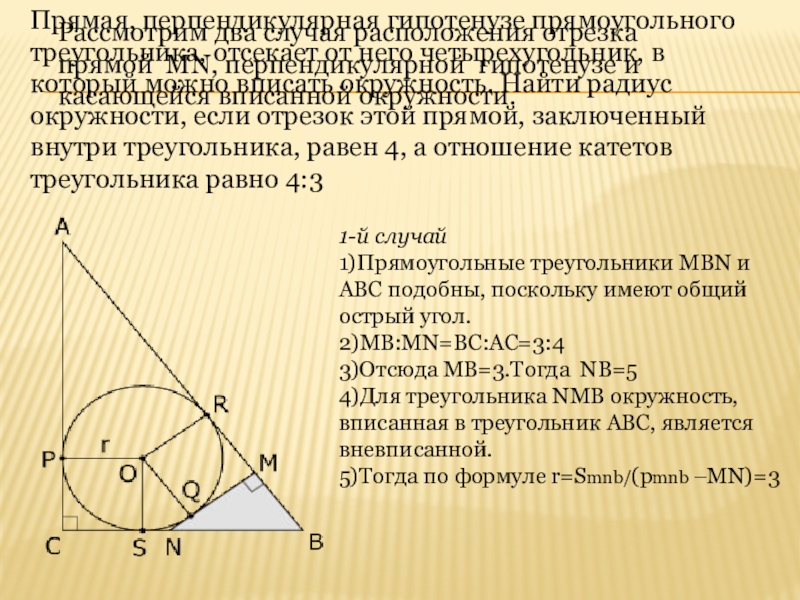
Слайд 12Прямая, перпендикулярная гипотенузе прямоугольного треугольника, отсекает от него четырехугольник, в который
1-й случай
1)Прямоугольные треугольники MBN и АВС подобны, поскольку имеют общий острый угол.
2)MB:MN=BC:AC=3:4
3)Отсюда MB=3.Тогда NB=5
4)Для треугольника NMB окружность,
вписанная в треугольник АВС, является
вневписанной.
5)Тогда по формуле r=Smnb/(pmnb –MN)=3
Рассмотрим два случая расположения отрезка прямой MN, перпендикулярной гипотенузе и касающейся вписанной окружности.
Слайд 132-й случай
1)Прямоугольные треугольники AMN и АВС
подобны, поскольку имеют общий острый
2)AM:MN=AC:BC=4:3
3)Отсюда AM=16/3.Тогда AN=20/3
4)Для треугольника MAN окружность, вписанная в треугольник АВС, является вневписанной.
5)Тогда по формуле r=Smna/(pmna –MN)=8/3
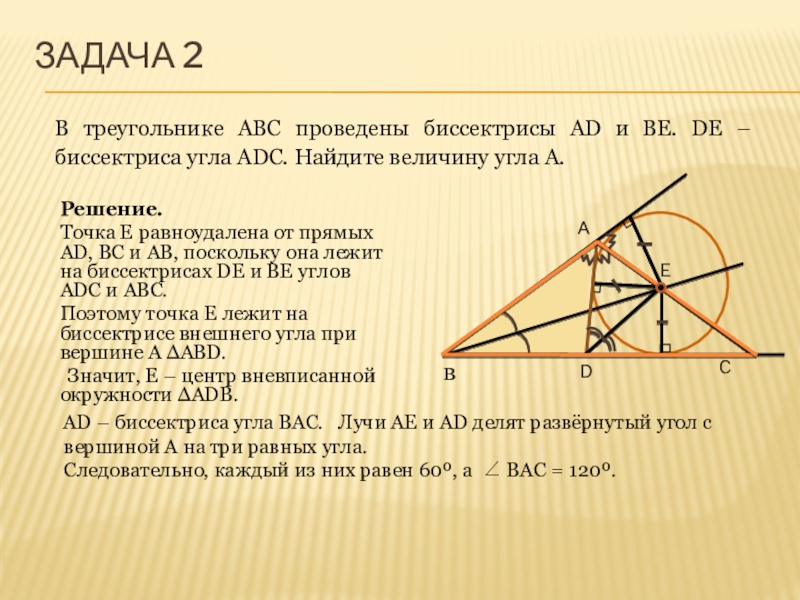
Слайд 14Задача 2
Решение.
Точка E равноудалена от прямых AD, BC и AB, поскольку
Поэтому точка E лежит на биссектрисе внешнего угла при вершине A ΔABD.
Значит, E – центр вневписанной окружности ΔADB.
AD – биссектриса угла BAC. Лучи AE и AD делят развёрнутый угол с вершиной A на три равных угла.
Следовательно, каждый из них равен 60º, а BAC = 120º.
В треугольнике ABC проведены биссектрисы AD и BE. DE – биссектриса угла ADC. Найдите величину угла A.