- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Первый признак равенства треугольников. Решение задач (7 класс)
Содержание
- 1. Презентация по геометрии на тему Первый признак равенства треугольников. Решение задач (7 класс)
- 2. АВС
- 3. ТРЕУГОЛЬНИК и его элементыA, B, C –
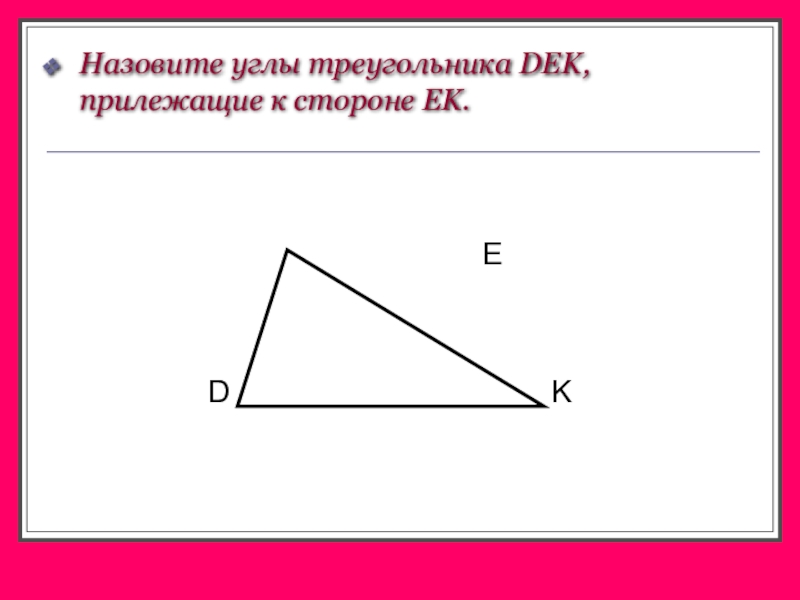
- 4. Назовите углы треугольника DEK, прилежащие к стороне EK.
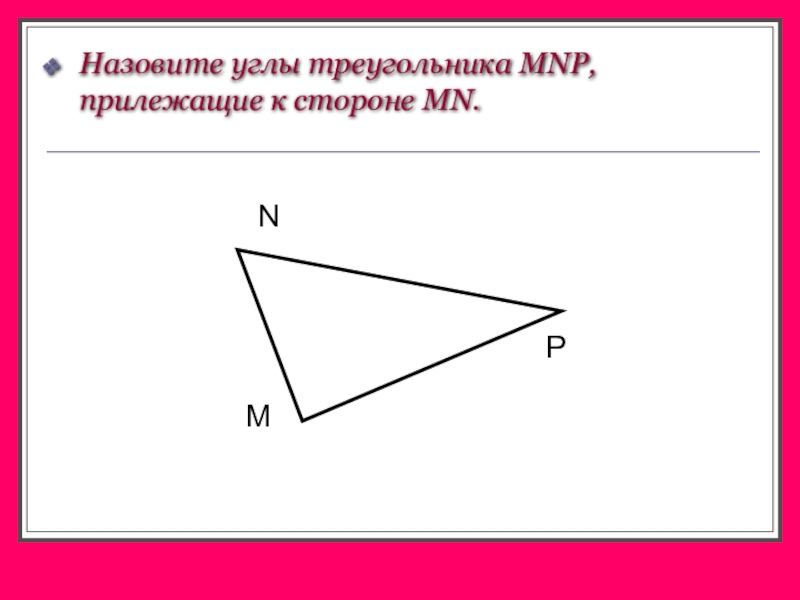
- 5. Назовите углы треугольника MNP, прилежащие к стороне MN.MPN
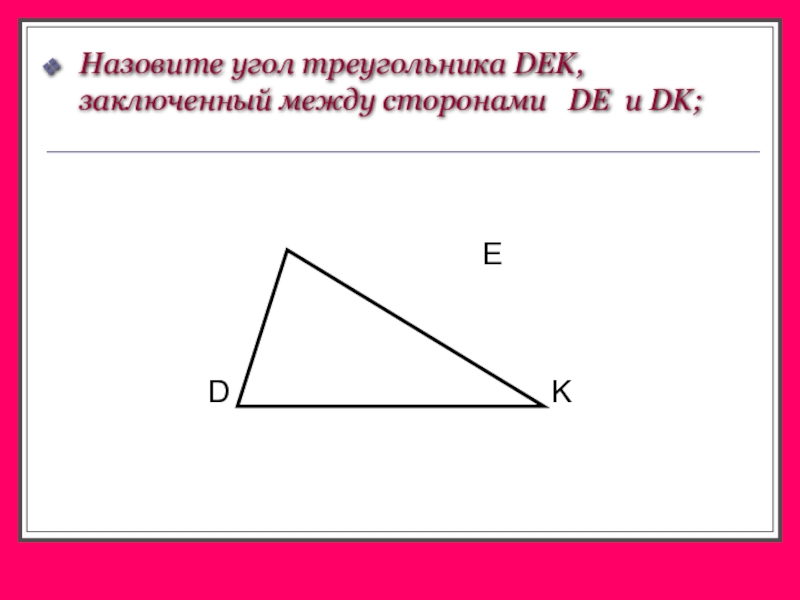
- 6. Назовите угол треугольника DEK, заключенный между сторонами DE и DK;
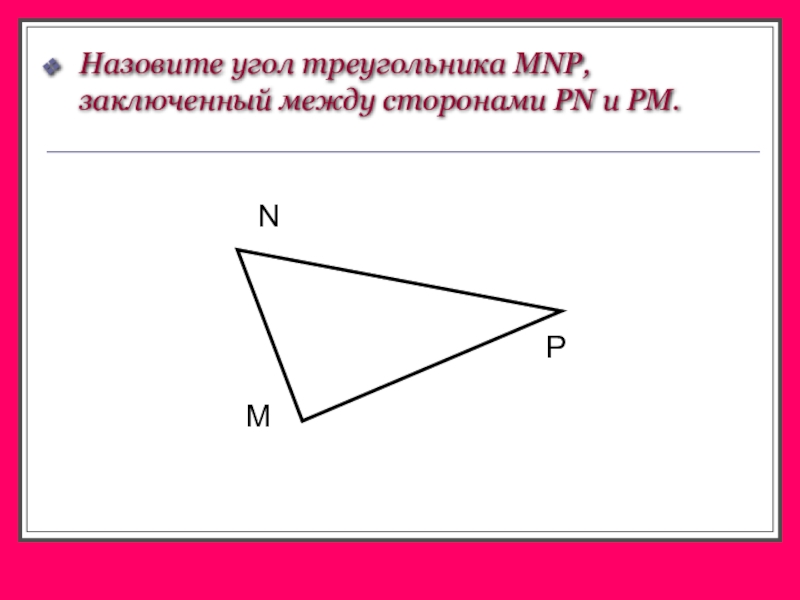
- 7. Назовите угол треугольника MNP, заключенный между сторонами РN и РМ.MPN
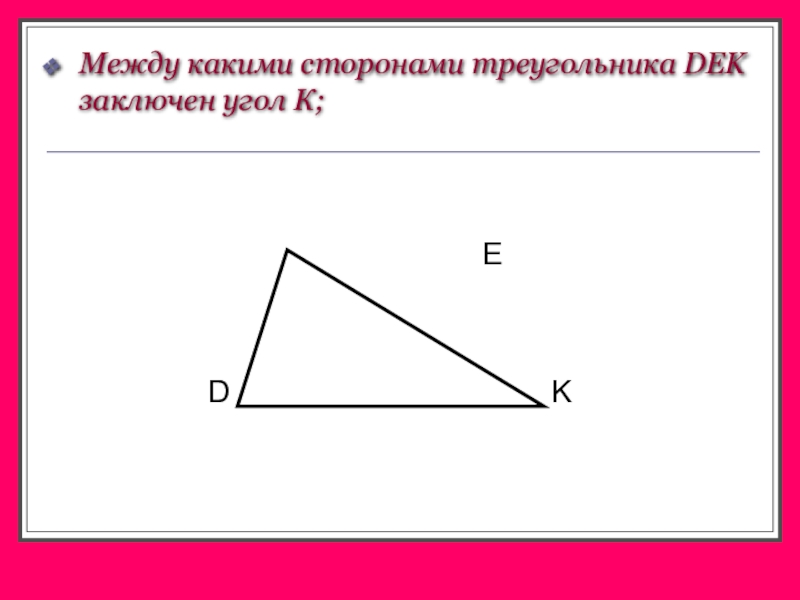
- 8. Между какими сторонами треугольника DEK заключен угол К;
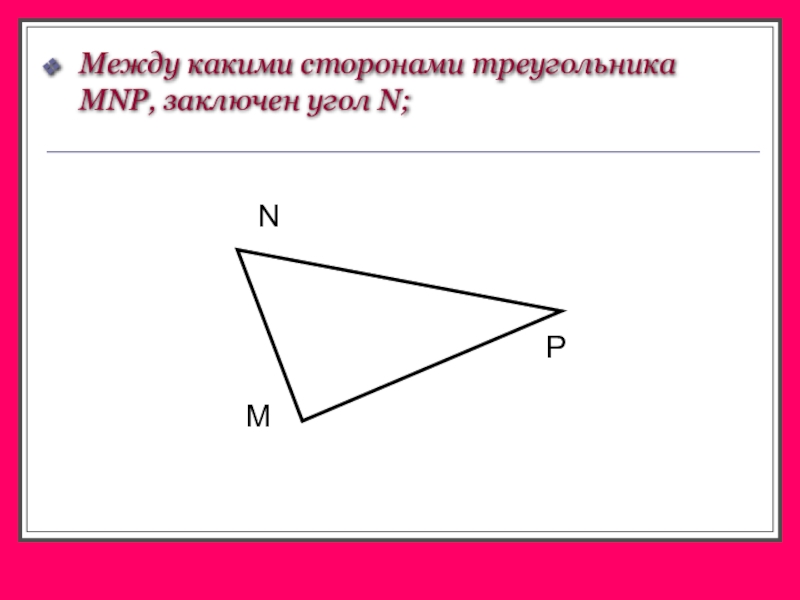
- 9. Между какими сторонами треугольника MNP, заключен угол N;MPN
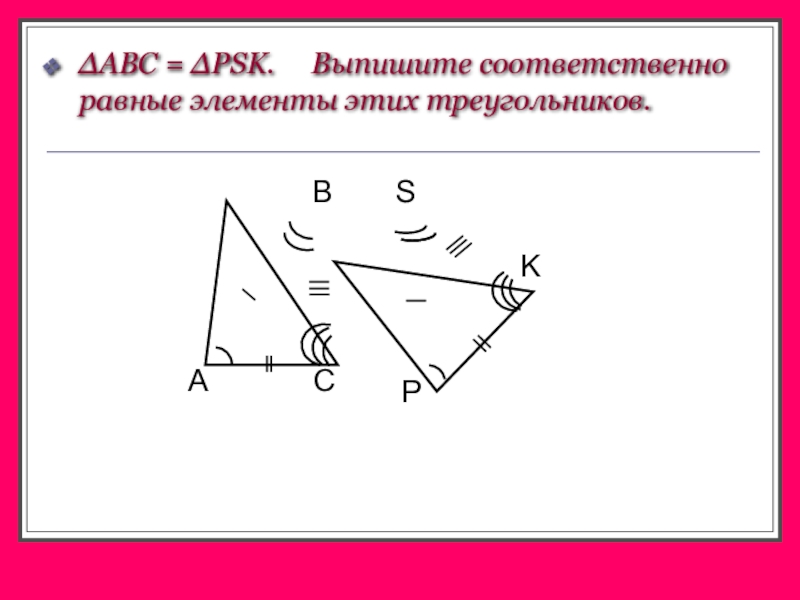
- 10. ∆ABC = ∆PSK. Выпишите соответственно равные элементы этих треугольников.SBACPK
- 11. ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВЕсли две стороны и
- 12. ТЕОРЕМАДано: ∆ABC и ∆A1B1C1 ∠ВAС =
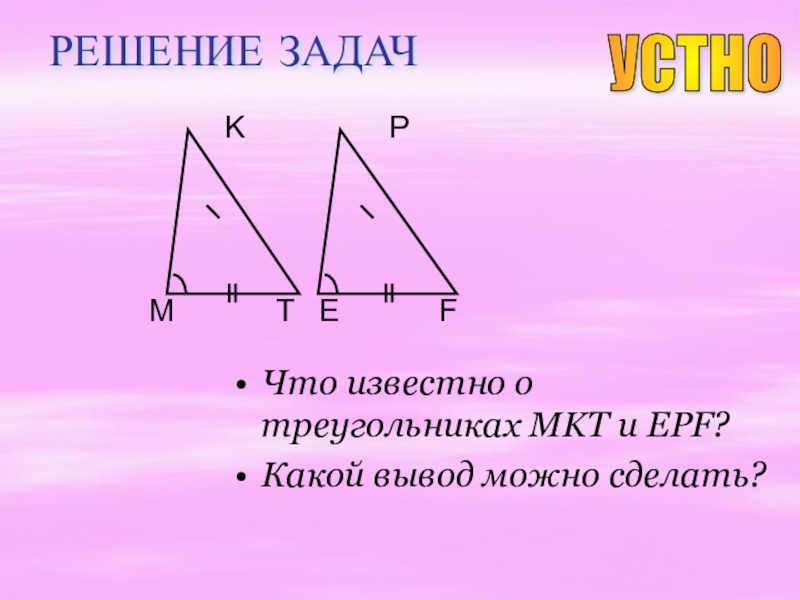
- 13. РЕШЕНИЕ ЗАДАЧЧто известно о треугольниках MKT и EPF?Какой вывод можно сделать?MTKEFPУСТНО
- 14. РЕШЕНИЕ ЗАДАЧЧто известно о треугольниках ABO и
- 15. ЗАДАЧА №3 (№94а)Дано: ∆ABD u ∆CDA; AB
- 16. ЗАДАЧА №3 (№94а)Дано: ∆ABD u ∆CDA; AB
- 17. ЗАДАЧА №4 (№95a)Дано: AD = BC; ∠1
- 18. ЗАДАЧА №4 (№95a)Дано: ВС = АD; ∠1
- 19. ЗАДАЧА №5Дано: AK = PM; ∠KAP =
- 20. ЗАДАЧА №5Дано: AK = PM; ∠KAP =
- 21. ЗАДАЧА №6Дано: AM = CN;AB = BC;
- 22. ЗАДАЧА №6Дано: AM = CN;AB = BC;
- 23. математическийдиктант
- 24. №1Закончить предложение∆ABC = ∆KPS по первому признаку,
- 25. №2Закончить предложение∆ABC = ∆EFM по первому признаку,
- 26. ДОМАШНЕЕ ЗАДАНИЕП14,15 вопросы 1-4 Теорему и доказательство учить;№95, 98
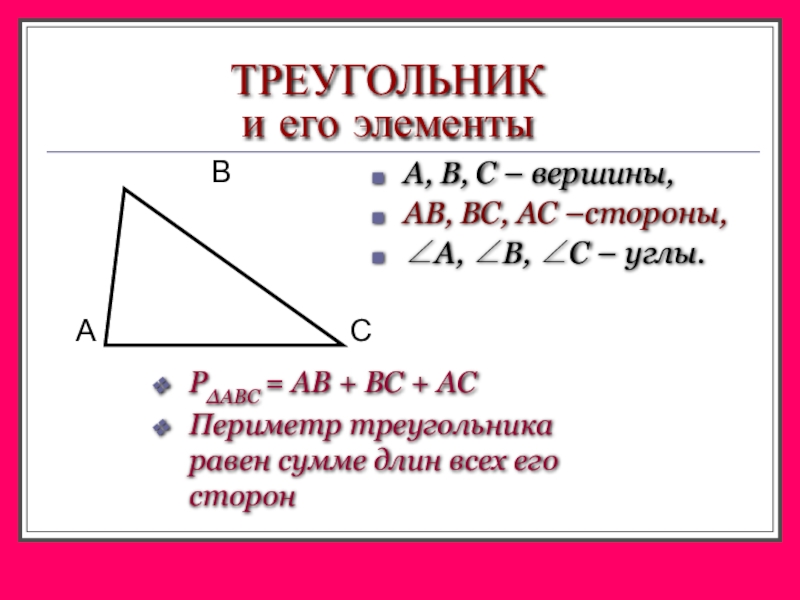
Слайд 3ТРЕУГОЛЬНИК
и его элементы
A, B, C – вершины,
АВ, ВС, АС –стороны,
∠A,
P∆ABC = AB + ВC + АC
Периметр треугольника равен сумме длин всех его сторон
Слайд 11ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Если две стороны и угол между ними одного
Слайд 12ТЕОРЕМА
Дано: ∆ABC и ∆A1B1C1
∠ВAС = ∠B1A1C1
AB = A1B1.
Доказать: ∆ABC = ∆A1B1C1
A
B
С
A1
B1
C1
Доказательство:
1.Так как ∠ВAС = ∠B1A1C1 , то ∆ABC можно наложить на ∆A1B1C1 , так что вершина А совместится с вершиной A1 , а стороны АВ и АС наложатся соответственно на лучи A1B1 и A1C1
2.Поскольку АВ = A1B1 , то сторона АВ совместится со стороной A1B1 , в частности, совместятся точки В и B1.
3.Поскольку АС = A1C1, то сторона АС совместится со стороной A1C1, в частности, совместятся точки С и C1. Следовательно, совместятся стороны ВС и В1C1.
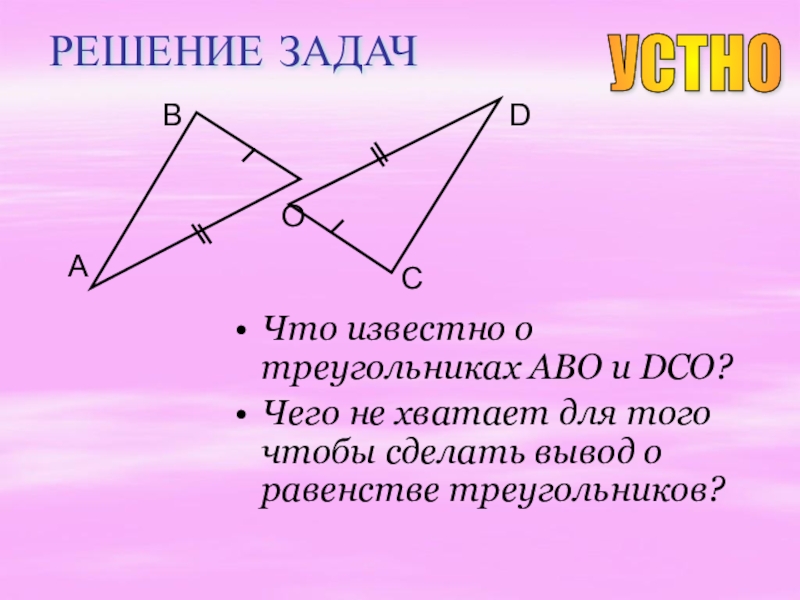
Слайд 14РЕШЕНИЕ ЗАДАЧ
Что известно о треугольниках ABO и DCO?
Чего не хватает для
A
B
O
C
D
УСТНО
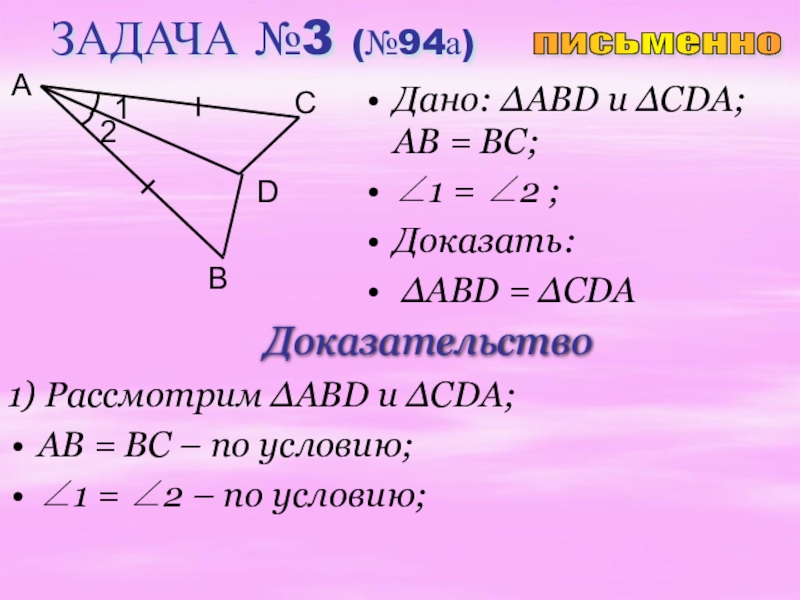
Слайд 15ЗАДАЧА №3 (№94а)
Дано: ∆ABD u ∆CDA; AB = BC;
∠1 =
Доказать:
∆ABD = ∆CDA
A
B
C
D
письменно
Доказательство
1) Рассмотрим ∆ABD и ∆CDA;
AB = BC – по условию;
∠1 = ∠2 – по условию;
2
1
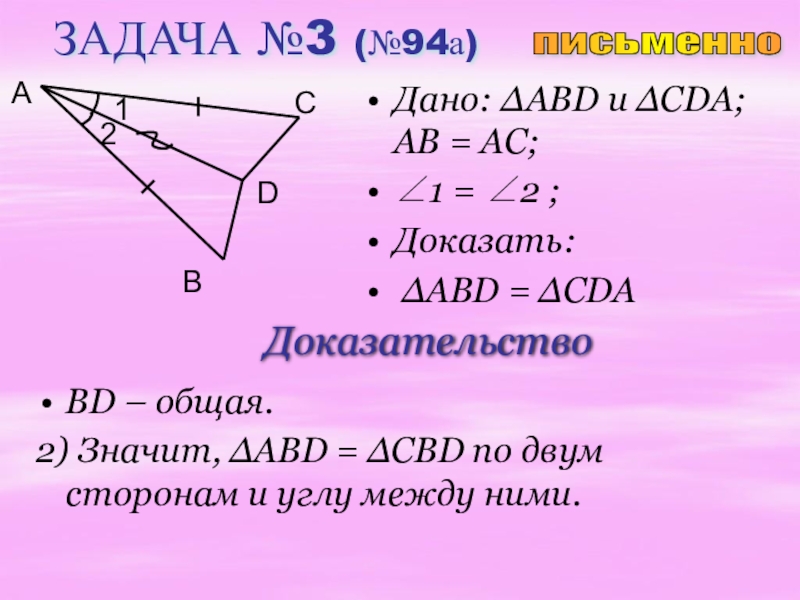
Слайд 16ЗАДАЧА №3 (№94а)
Дано: ∆ABD u ∆CDA; AB = АC;
∠1 =
Доказать:
∆ABD = ∆CDA
A
B
C
D
письменно
Доказательство
BD – общая.
2) Значит, ∆ABD = ∆CBD по двум сторонам и углу между ними.
2
1
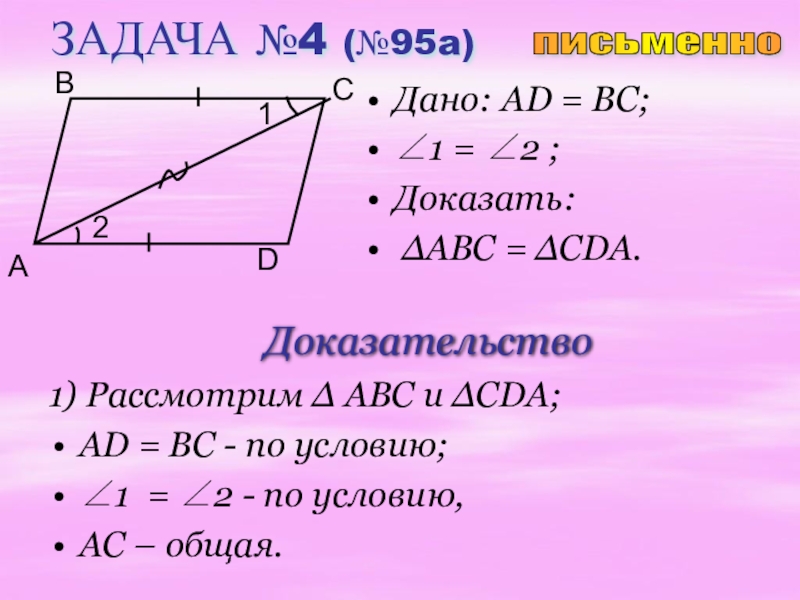
Слайд 17ЗАДАЧА №4 (№95a)
Дано: AD = BC;
∠1 = ∠2 ;
Доказать:
A
B
C
D
письменно
Доказательство
1) Рассмотрим ∆ ABC и ∆CDA;
AD = BC - по условию;
∠1 = ∠2 - по условию,
AC – общая.
1
2
Слайд 18ЗАДАЧА №4 (№95a)
Дано: ВС = АD;
∠1 = ∠2 ;
Доказать:
A
B
C
D
письменно
Доказательство
2) Значит, ∆ABC = ∆CDA по двум сторонам и углу между ними.
1
2
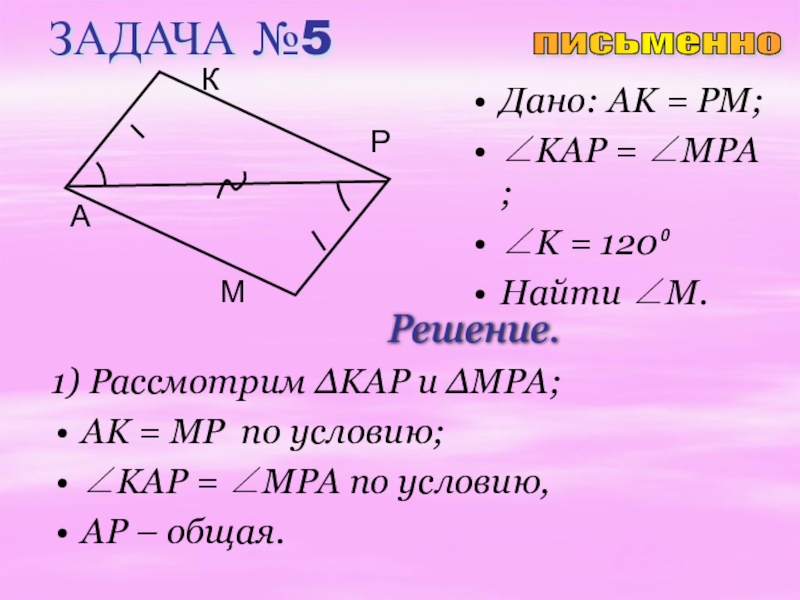
Слайд 19ЗАДАЧА №5
Дано: AK = PM;
∠KAP = ∠MPA ;
∠K =
Найти ∠M.
A
К
Р
М
письменно
Решение.
1) Рассмотрим ∆KAP и ∆MPA;
AK = MP по условию;
∠KAP = ∠MPA по условию,
AP – общая.
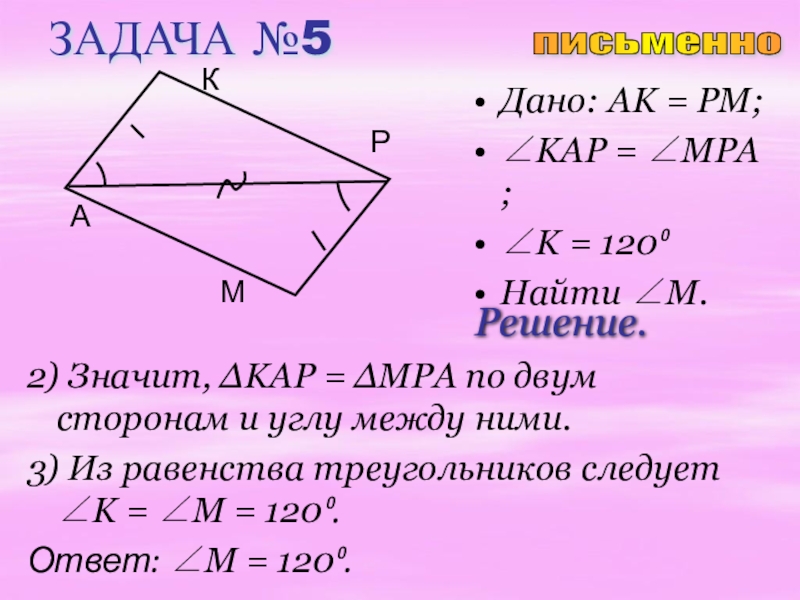
Слайд 20ЗАДАЧА №5
Дано: AK = PM;
∠KAP = ∠MPA ;
∠K =
Найти ∠M.
A
К
Р
М
письменно
2) Значит, ∆KAP = ∆MPA по двум сторонам и углу между ними.
3) Из равенства треугольников следует ∠K = ∠M = 120⁰.
Ответ: ∠M = 120⁰.
Решение.
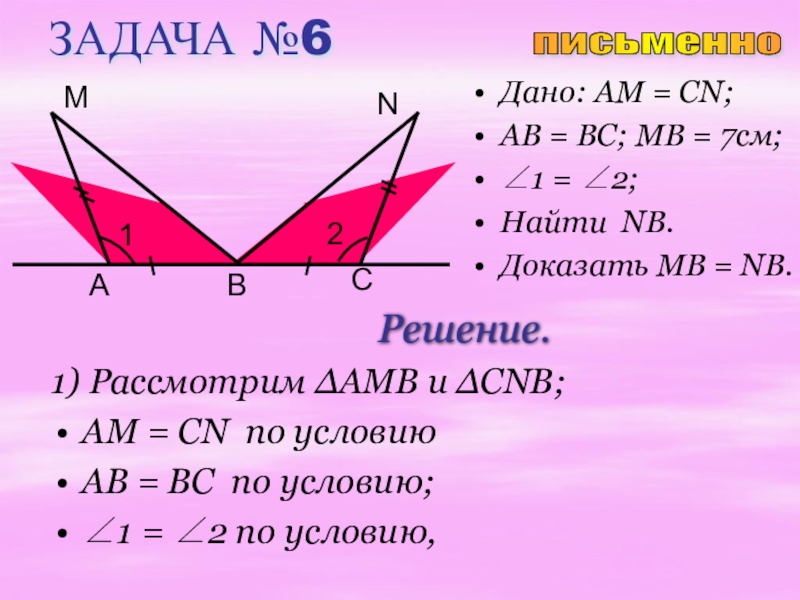
Слайд 21ЗАДАЧА №6
Дано: AM = CN;
AB = BC; MB = 7см;
∠1 =
Найти NB.
Доказать MB = NB.
A
В
N
М
письменно
Решение.
1) Рассмотрим ∆AMB и ∆CNB;
AM = CN по условию
AB = BC по условию;
∠1 = ∠2 по условию,
C
2
1
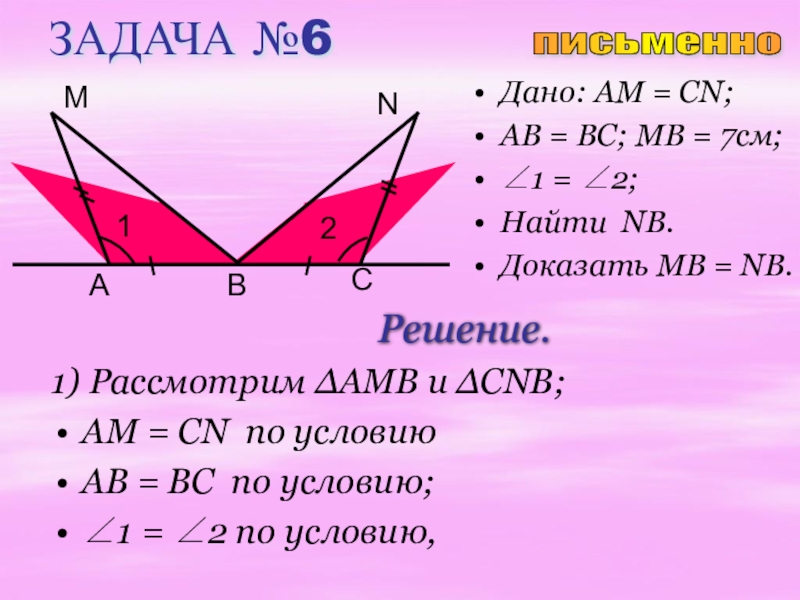
Слайд 22ЗАДАЧА №6
Дано: AM = CN;
AB = BC; MB = 7см;
∠1 =
Найти NB.
Доказать MB = NB.
A
В
N
М
письменно
Решение.
1) Рассмотрим ∆AMB и ∆CNB;
AM = CN по условию
AB = BC по условию;
∠1 = ∠2 по условию,
C
2
1
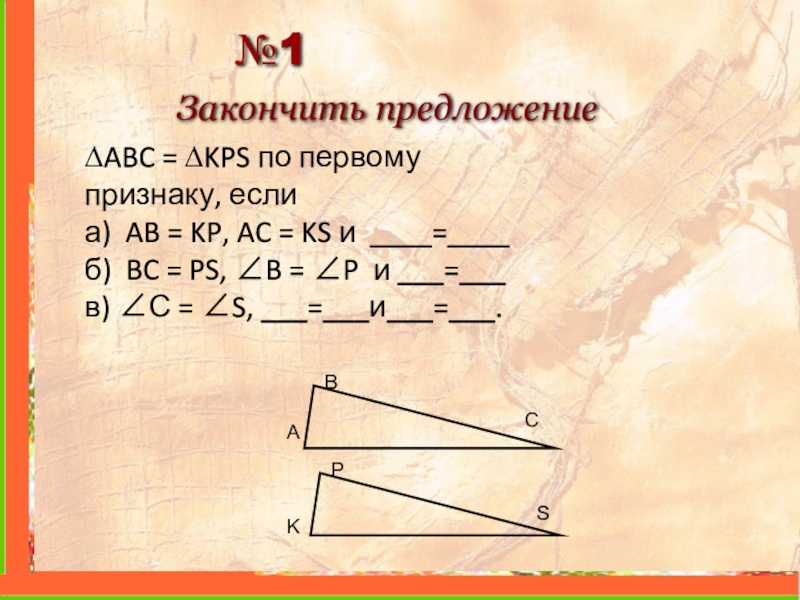
Слайд 24№1
Закончить предложение
∆ABC = ∆KPS по первому признаку, если
а) AB = KP,
б) BC = PS, ∠B = ∠P и ___=___
в) ∠С = ∠S, ___=___и___=___.
Слайд 25№2
Закончить предложение
∆ABC = ∆EFM по первому признаку, если
а) AB = EF,
б) BC = FM, ∠B = ∠F и ___=___
в) ∠С = ∠M, ___=___, ___=___.