- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Некоторые доказательства теоремы Пифагора к уроку по геометрии на тему Теорема Пифагора
Содержание
- 1. Презентация Некоторые доказательства теоремы Пифагора к уроку по геометрии на тему Теорема Пифагора
- 2. Доказательства Теоремы ПифагораКвадрат,построенный на гипотенузе прямоугольного треугольника,равновелик сумме квадратов,построенных на его катетах
- 3. ПифагорИсторию жизни Пифагора трудно отделить от легенд.Ещё
- 4. Школа Пифагора дала Греции целую плеяду талантливых
- 5. Теорема Пифагора — одна из
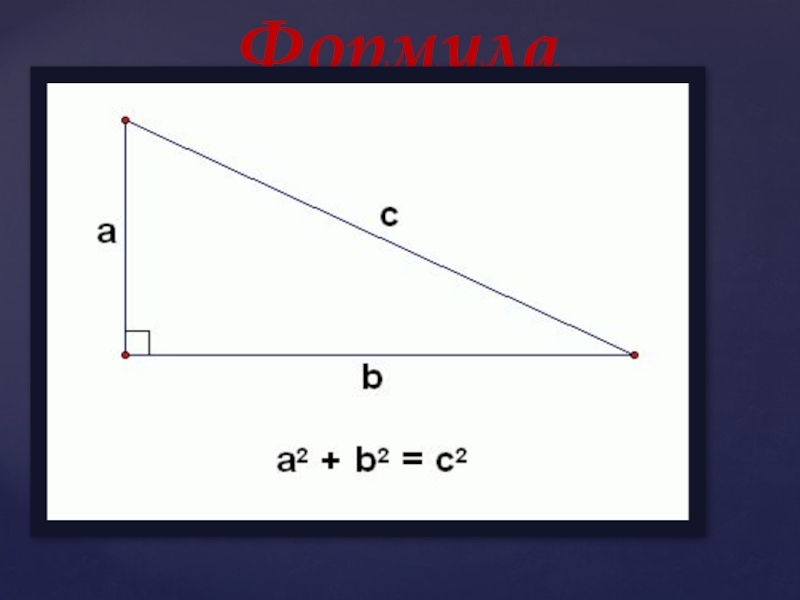
- 6. Формула
- 7. Слайд 7
- 8. Доказательства теоремыНа данный момент в научной литературе зафиксировано 367 доказательств данной теоремыДоказательство через подобные треугольники
- 9. Доказательство из учебника геометрии 7-9 классРассмотрим прямоугольный
- 10. Доказательство древнеиндийского математика БхаскариПостройте прямоугольный треугольник со
- 11. Внутри квадрата постройте четыре прямоугольных треугольника так,
- 12. Главные элементы доказательства — симметрия и движение.
- 13. Доказательство ЕвклидаДоказательство Евклида приведено в предложении
- 14. Читается так:Теорема,обратная теореме ПифагораЕсли квадрат одной стороны треугольника равен сумме квадратов двух других сторон,то треугольник прямоугольный
- 15. Итак, теорема Пифагора - одна из главных
Слайд 1Государственное Бюджетное Общеобразовательное Учреждение Средняя Общеобразовательная школа №664 г.Москва Некоторые доказательства теоремы Пифагора Габоян
Руководитель: Лазуткина Оксана Владимировна
Слайд 2Доказательства
Теоремы Пифагора
Квадрат,построенный на гипотенузе прямоугольного треугольника,равновелик сумме квадратов,построенных на его катетах
Слайд 3Пифагор
Историю жизни Пифагора трудно отделить от легенд.
Ещё Геродот называл его «величайшим
Родом из Тарента, где сильны были позиции пифагорейцев. Таким образом, самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.
Слайд 4Школа Пифагора дала Греции целую плеяду талантливых философов, физиков и математиков.
Школа Пифагора
Слайд 5 Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии,
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Читается теорема так:
Слайд 7 Исследование доказательств теоремы Пифагора: Самое трудное доказательство теоремы – доказательство Евклида Самое известное
Слайд 8Доказательства теоремы
На данный момент в научной литературе зафиксировано 367 доказательств данной
Доказательство через подобные треугольники
Слайд 9Доказательство из учебника геометрии 7-9 класс
Рассмотрим прямоугольный треугольник с катетами а,
С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна ½ а·в, и квадрата со стороной с, поэтому: S=4·½ ав+с ²= 2ав+с².
Таким образом:(а+в) ² =2ав+с ², откуда: с ² =а ² +в ².Теорема доказана.
Слайд 10Доказательство древнеиндийского математика Бхаскари
Постройте прямоугольный треугольник со сторонами a, b и
В первом квадрате постройте четыре таких же треугольника, как на рисунке 1. В результате получаться два квадрата: один со стороной a, второй со стороной b. Во втором квадрате четыре треугольника образуют квадрат со стороной, равной гипотенузе c. Сумма площадей построенных квадратов на рис.2 равна площади построенного нами квадрата со стороной с на рис.3. Это легко проверить, высчитав площади квадратов на рис. 2 по формуле. А площадь вписанного квадрата на рисунке 3. путем вычитания площадей четырех равных между собой вписанных в квадрат прямоугольных треугольников из площади большого квадрата со стороной (a+b).
Записав все это, имеем: a²+b²=(a+b)² – 4.
Слайд 11Внутри квадрата постройте четыре прямоугольных треугольника так, как это обозначено на
Вы можете использовать оба варианта вычисления площади квадрата, чтобы убедиться: они дадут одинаковый результат. И это дает вам право записать, что
c²=(a-b)²+4 · 1:2 · a · b. В результате решения вы получите формулу теоремы Пифагора c²=a²+b². Теорема доказана.
Древнеиндийское доказательство
Слайд 12Главные элементы доказательства — симметрия и движение. Рассмотрим чертёж, как видно
Доказательство
Леонардо Да Винчи
Слайд 13 Доказательство Евклида
Доказательство Евклида приведено в предложении 47 первой книги "Начал".
Слайд 14Читается так:
Теорема,обратная теореме Пифагора
Если квадрат одной стороны треугольника равен сумме квадратов
Слайд 15Итак, теорема Пифагора - одна из главных и, можно сказать, самая
c² =a² +b² . Поэтому для её доказательства часто используют наглядность.
Заключение