и вписанные углы
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Центральные и вписанные углы геометрия 8 класс
Содержание
- 1. Центральные и вписанные углы геометрия 8 класс
- 2. Дуга окружностиМ
- 3. Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности.
- 4. Чем похожи и чем различаются углы АОВ
- 5. Дугу окружности можно измерять в градусах.Если дуга
- 6. Слайд 6
- 7. АВЕсли дуга АВ окружности с центром О больше полуокружности, то ее градусная мера считается равной6502950650
- 8. АВСD1150300
- 9. M3000600АВНайти
- 10. M2720880АВНайти угол АОВ.?880
- 11. ВАНайти расстояние от точки А до радиуса ОВ. R = 6.6006006Х
- 12. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним. АВСК12=+Повторение
- 13. ОТеорема. Вписанный угол измеряется половиной
- 14. ОВписанный угол измеряется половиной дуги, на которую он опирается.1 случай2a2a
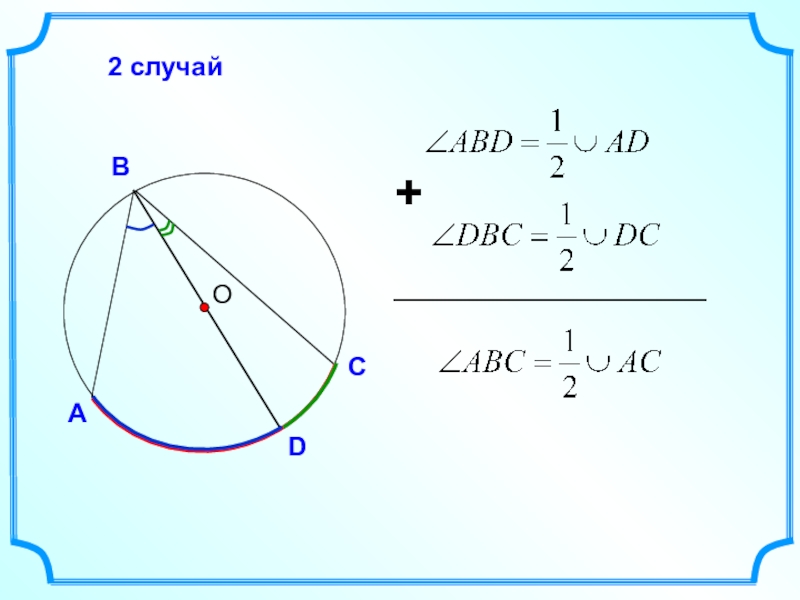
- 15. ОАСВ2 случайD
- 16. ОАСВ3 случайD
- 17. ОВписанные углы, опирающиеся на одну и ту же дугу, равны.Следствие 1ВNM
- 18. ОВписанный угол, опирающийся на полуокружность – прямой.Следствие 2ВА
- 19. Блиц-опросАСВНайдите градусную меру угла АВС1100 О1100550
- 20. Блиц-опросАСВНайдите градусную меру угла АВС1200 О120024001200
- 21. Найдите градусную меру угла АВС.ОВАСБлиц-опрос
- 22. Блиц-опросАDВНайдите градусную меру угла АВС5001000С26001300 О
Дуга окружностиМ
Слайд 3Дуга называется полуокружностью, если отрезок,
соединяющий ее концы, является диаметром окружности.
Слайд 4Чем похожи и чем различаются углы АОВ и АСВ?
Центральный угол
Вписанный угол
Составьте
определение этих углов.
Угол с вершиной в центре окружности называется центральным углом.
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
Слайд 5Дугу окружности можно измерять в градусах.
Если дуга АВ окружности с центром
О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ.
650
650
Слайд 7
А
В
Если дуга АВ окружности с центром О больше полуокружности, то ее
градусная мера считается равной
650
2950
650
Слайд 12
Внешний угол треугольника равен сумме
двух углов треугольника, не смежных с
ним.
А
В
С
К
1
2
=
+
Повторение
Слайд 13 О
Теорема. Вписанный угол измеряется половиной
дуги, на которую он опирается.
2a
2a
= a
2a
Тогда внешний угол АОС =