«СОШ №87» г. Северск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по геометрии на тему Симметрия (8 класс)
Содержание
- 1. Презентация к уроку по геометрии на тему Симметрия (8 класс)
- 2. «Стоя перед черной доской и рисуя
- 3. Обобщить и расширить представления о симметрии. Рассмотреть
- 4. от греческого symmetria - "соразмерность" понятие, означающее сохраняемость, повторяемость, порядок и красоту.Симметрия
- 5. Две точки А и А1
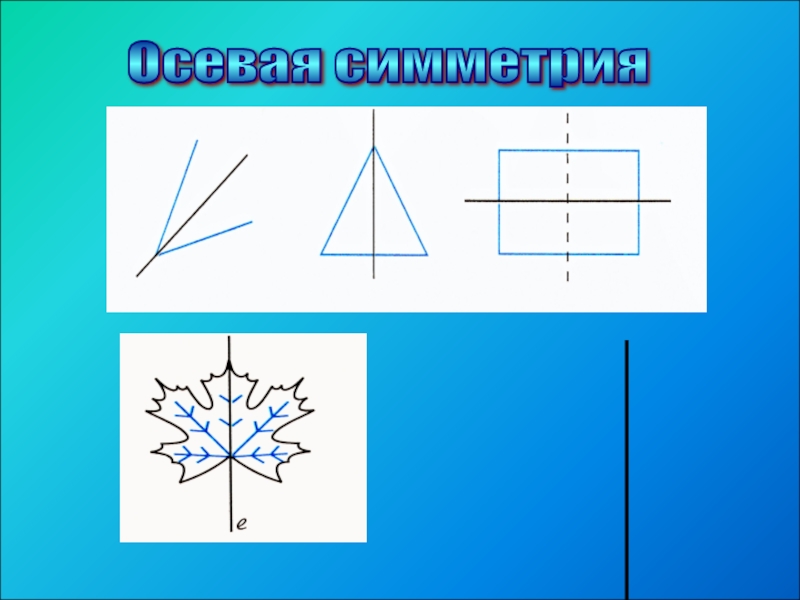
- 6. Осевая симметрия
- 7. Две точки А и А1 называются симметричными
- 8. Центральная симметрия
- 9. 1. Если отрезки АО и ОВ
- 10. 3. Существуют фигуры, которые имеют два центра
- 11. 6. Фигура симметричная четырехугольнику относительно некоторой прямой,
- 12. 9. Если даны две точки, то
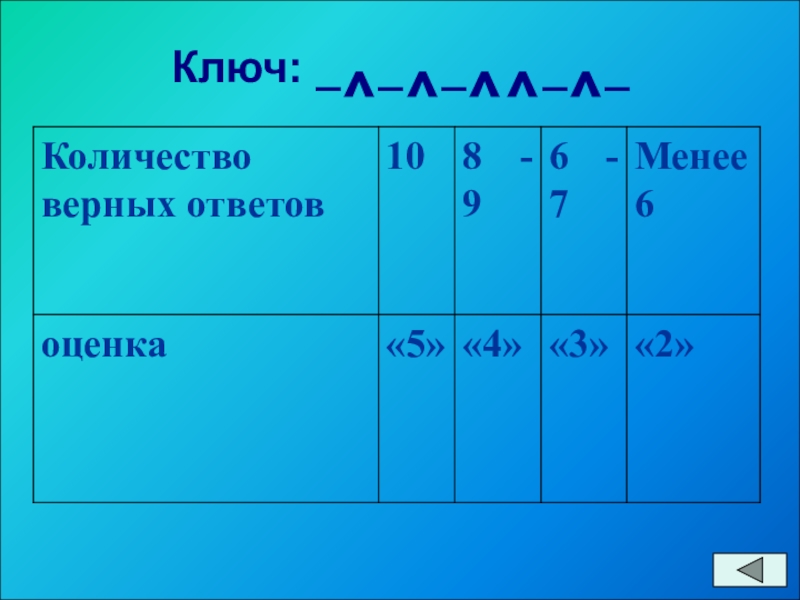
- 13. Ключ: _^_^_^^_^_
- 14. Если при переносе плоской фигуры F вдоль
- 15. Бордюры и орнаменты
- 16. Симметрия в архитектуре
- 17. Симметрия широко встречается в природе, в особенности
- 18. Принципы симметрии являются в физике инструментом для
- 19. В XX веке усилиями российских учёных -
- 20. У цветковых растений в большинстве проявляется радиальная
- 21. Симметрия обнаруживается также и на
- 22. Под симметрией у животных понимают соответствие в
- 23. Тело человека построено по принципу двусторонней симметрии
- 24. Гипотеза профессора Е. В. Черносвистова:Лица умерших людей
- 25. Симметрия в природе (растениях, животных, минералах и
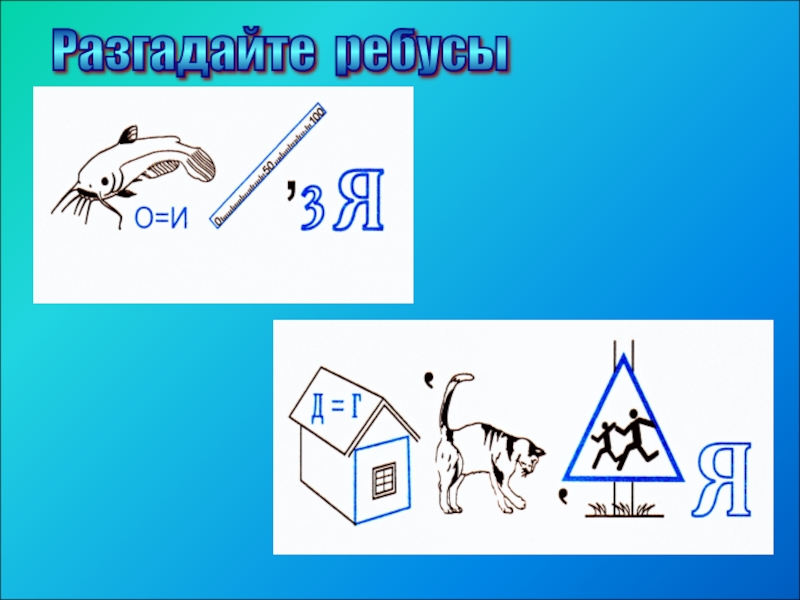
- 26. Разгадайте ребусы
- 27. Буквы разбиты на группы. Требуется определить принцип,
- 28. Определите какая симметрия используется в рисовании этих
- 29. Заполните свободные части рисунков числами и
- 30. -0,05
- 31. Каким видом симметрии обладает данная фигура? Сколько
- 32. Математика выявляет порядок, симметрию и определенность, а
- 33. Спасибо за урок
«Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно
Слайд 2
«Стоя перед черной доской и рисуя на ней мелом разные
фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?»
Лев Николаевич Толстой
Лев Николаевич Толстой
Слайд 3
Обобщить и расширить представления о симметрии. Рассмотреть проявление симметрии в природе,
различных областях науки, архитектуре и искусстве.
Цель
Структура урока
Временные затраты
Слайд 4
от греческого symmetria - "соразмерность"
понятие, означающее сохраняемость, повторяемость, порядок и
красоту.
Симметрия
Слайд 5
Две точки А и А1 называют симметричными относительно прямой
а если эта прямая проходит через середину отрезка А А1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Осевая симметрия
Слайд 7
Две точки А и А1 называются симметричными относительно точки О, если
О-середина отрезка АА1. Точка О считается симметричной самой себе.
Центральная симметрия
Слайд 9
1. Если отрезки АО и ОВ равны, то точки А
и В являются симметричными относительно точки О.
2. Если точки А и В симметричны относительно точки О, то все эти три точки лежат на одной прямой.
Условные обозначения: «да» - ^, «нет» _
Тест
Слайд 10
3. Существуют фигуры, которые имеют два центра симметрии.
4. Верно ли, что
квадрат имеет 4 оси симметрии?
5. Существует треугольник, у которого есть центр симметрии.
Тест
Слайд 11
6. Фигура симметричная четырехугольнику относительно некоторой прямой, является четырехугольником.
7.Верно ли, что
симметричные фигуры равны?
8. Фигура не может иметь более 4 осей симметрии.
Тест
Слайд 12
9. Если даны две точки, то всегда можно найти
прямую, относительно которой они симметричны.
10. Треугольник имеет хотя бы одну ось симметрии.
Тест
Слайд 14
Если при переносе плоской фигуры F вдоль заданной прямой АВ на
расстояние а (или кратное этой величине) фигура совмещается сама с собой, то говорят о переносной симметрии. Прямая АВ называется осью переноса, расстояние а элементарным переносом или периодом.
Переносная симметрия
Слайд 17
Симметрия широко встречается в природе, в особенности у кристаллов, у растений
и животных, например симметрия цветка, листа или морской звезды. Поразительные по красоте примеры симметрии дают снежинки.
Симметрия в природе
Слайд 18
Принципы симметрии являются в физике инструментом для отыскания новых законов природы.
К числу симметричных принципов относится принцип относительности Галилея и Эйнштейна
Симметрия в физике
Слайд 19
В XX веке усилиями российских учёных - В Беклемишева, В Вернадского,
В Алпатова, Г.Гаузе - было создано новое направление в учении о симметрии - биосимметрика
На примере дерева просматривается симметрия конуса
Симметрия в биологии
Слайд 20У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок
считается симметричным, когда каждый околоцветник состоит из равного числа частей.
У цветковых растений в большинстве проявляется радиальная и билатеральная симметрия. Цветок считается симметричным, когда каждый околоцветник состоит из равного числа частей.
Симметрия в биологии
Слайд 21
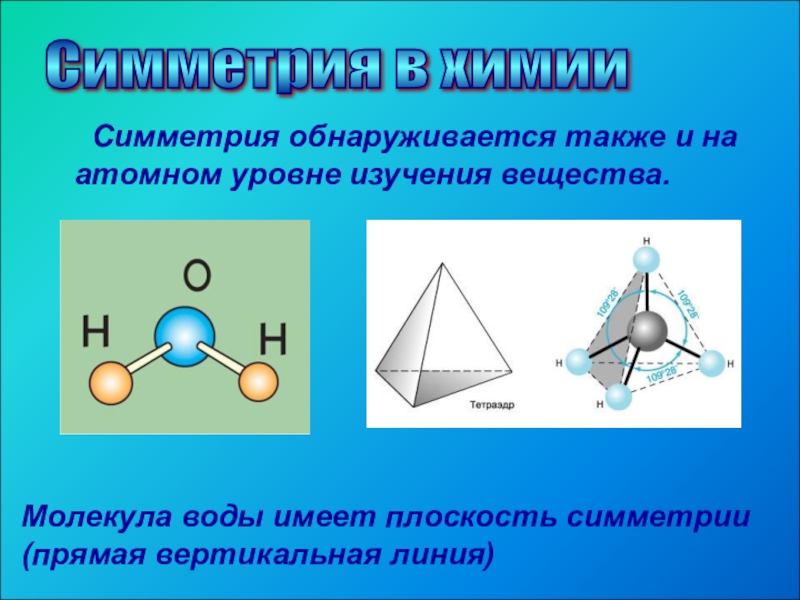
Симметрия обнаруживается также и на атомном уровне изучения вещества.
Молекула воды имеет плоскость симметрии (прямая вертикальная линия)
Симметрия в химии
Слайд 22Под симметрией у животных понимают соответствие в размерах, форме и очертаниях,
а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.
Под симметрией у животных понимают соответствие в размерах, форме и очертаниях, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии.
Симметрия у животных
радиальная (лучистая)
билатеральная
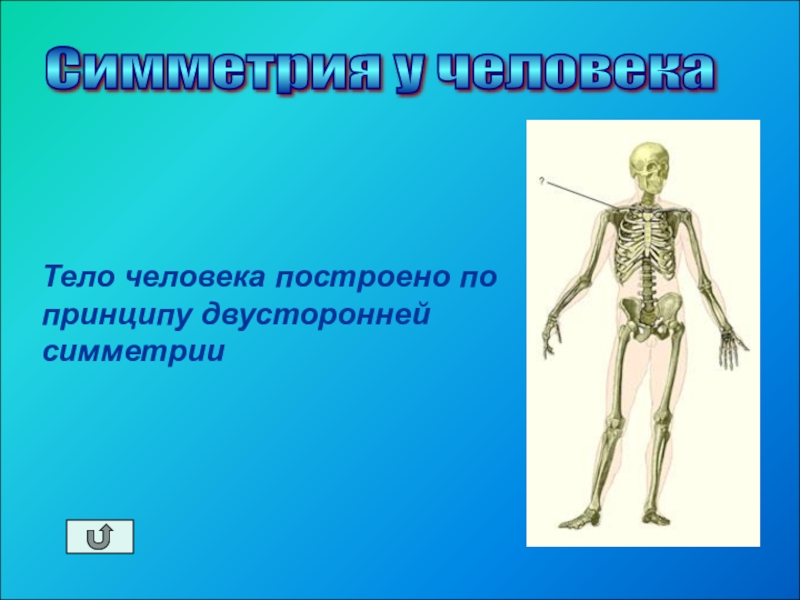
Слайд 23Тело человека построено по принципу двусторонней симметрии
Симметрия у человека
Тело человека
построено по принципу двусторонней симметрии
Слайд 24Гипотеза профессора Е. В. Черносвистова:
Лица умерших людей абсолютно симметричны. Лица молодых
и здоровых имеют выраженную асимметрию. С течением жизни она уменьшается. Полная же симметрия лица свидетельствует о наступлении смерти.
Симметрия у человека
Гипотеза профессора Е. В. Черносвистова:
Лица умерших людей абсолютно симметричны. Лица молодых и здоровых имеют выраженную асимметрию. С течением жизни она уменьшается. Полная же симметрия лица свидетельствует о наступлении смерти.
Слайд 25Симметрия в природе (растениях, животных, минералах и т.д);
Симметрия в искусстве (архитектуре,
живописи, поэзии, музыке);
Симметрия в орнаментах и бордюрах разных народов.
Симметрия в архитектуре и
зодчестве г.Томска.
Симметрия в орнаментах и бордюрах разных народов.
Симметрия в архитектуре и
зодчестве г.Томска.
Симметрия в природе (растениях, животных, минералах и т.д);
Симметрия в искусстве (архитектуре, живописи, поэзии, музыке);
Симметрия в орнаментах и бордюрах разных народов.
Симметрия в архитектуре и
зодчестве г.Томска.
Возможные темы исследований
Слайд 27Буквы разбиты на группы. Требуется определить принцип, по которому произведена эта
разбивка:
Буквы разбиты на группы. Требуется определить принцип, по которому произведена эта разбивка:
Задание
1 группа – А, Д, Л, М, П, Т, Ф, Ш;
2 группа - В, Е, З, К, С, Э, Ю;
3 группа – Ж, И, О, Х, Н;
4 группа – Б, Г, Р, У, Ц, Ч, Ь, Ы,Я,
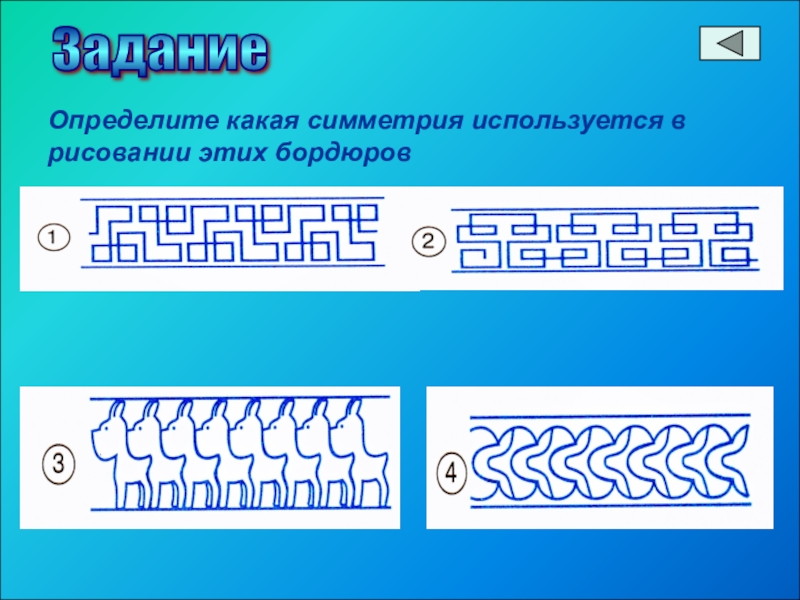
Слайд 28Определите какая симметрия используется в рисовании этих бордюров
Определите какая симметрия
используется в рисовании этих бордюров
Задание
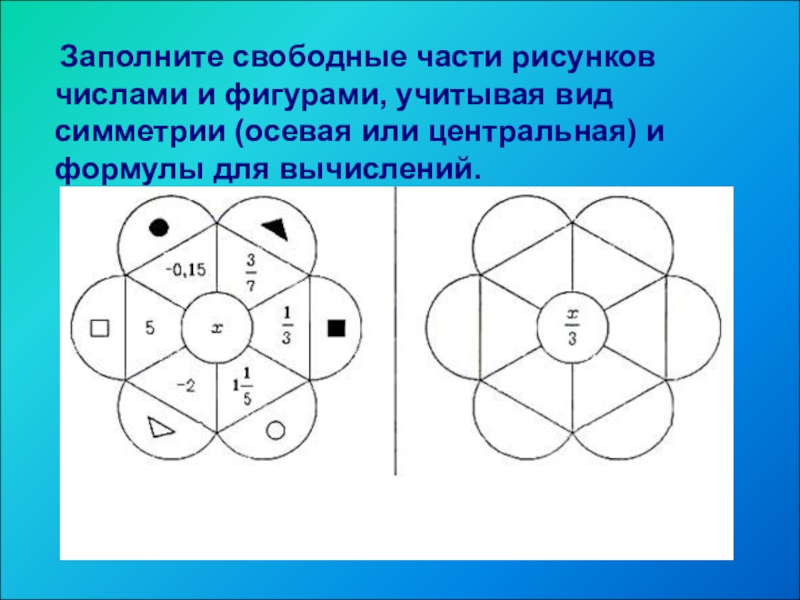
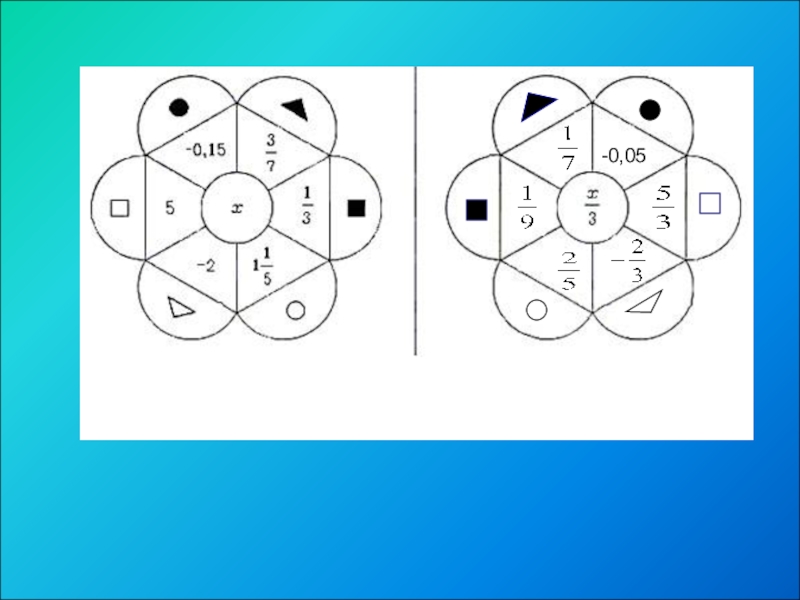
Слайд 29
Заполните свободные части рисунков числами и фигурами, учитывая вид симметрии
(осевая или центральная) и формулы для вычислений.
Слайд 31Каким видом симметрии обладает данная фигура? Сколько изображено квадратов?
Выберите нужный
ответ.
А) 8
б) 10
в) 7
А) 8
б) 10
в) 7
Каким видом симметрии обладает данная фигура? Сколько изображено квадратов?
Выберите нужный ответ.
А) 8
б) 10
в) 7
Задание
Слайд 32
Математика выявляет порядок, симметрию и определенность, а это - важнейшие виды
прекрасного.
Аристотель
Аристотель
Математика выявляет порядок, симметрию и определенность, а это - важнейшие виды прекрасного.
Аристотель
