- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Пособие по математике и геометрии
Содержание
- 1. Презентация по математике Пособие по математике и геометрии
- 2. Алгебра Алгебра - раздел математики, который можно грубо
- 3. ГеометрияГеометрия-раздел математики, изучающий пространственные структуры и отношения, а
- 4. Основные формулы в алгебре Степень с натуральным
- 5. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и
- 6. Степень с целым показателем. (- n)-й степенью (n –
- 7. Формулы сокращенного умножения (ФСУ).(a+b)2=a2+2ab+b2 Квадрат суммы двух выражений равен
- 8. Решение неполных квадратных уравнений.ax2=0 – неполное квадратное уравнение (b=0, c=0). Решение:
- 9. Решение полных квадратных уравнений. ax2+bx+c=0 – квадратное уравнение общего вида Дискриминант D=b2—
- 10. Основные формулы в геометрии Теорема Пифагора. Площадь параллелограмма. Значения синуса, косинуса, тангенса, котангенса Таблица БрадисаТеорема Фалеса
- 11. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b².
- 12. Признаки параллелограмма.Если две противоположные стороны четырехугольника параллельны
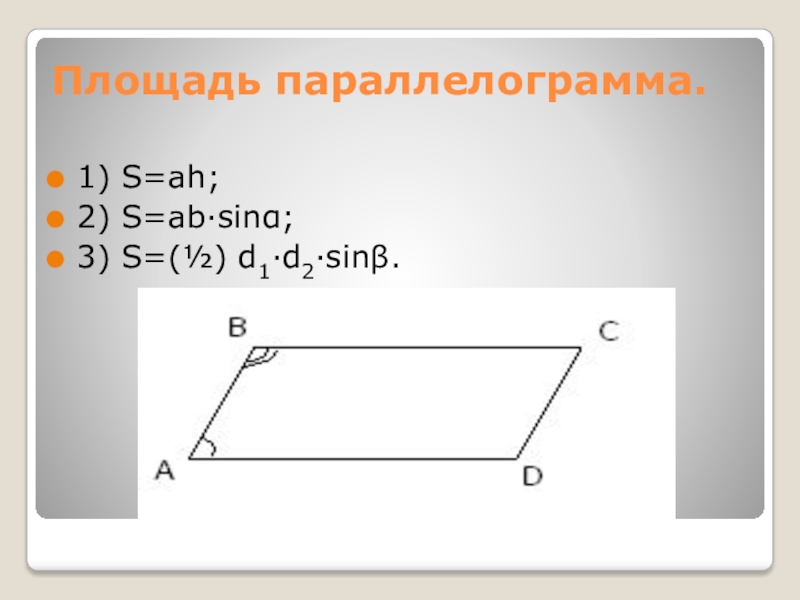
- 13. Площадь параллелограмма. 1) S=ah;2) S=ab∙sinα;3) S=(½) d1∙d2∙sinβ.
- 14. Значения синуса, косинуса, тангенса, котангенса Синусом угла α
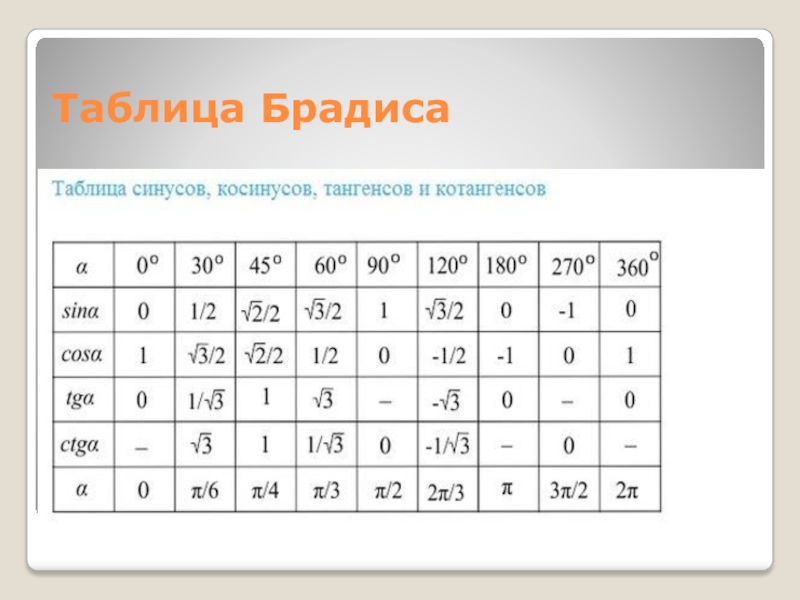
- 15. Таблица Брадиса
- 16. Теорема Фалеса Если параллельные прямые, пересекающие стороны
- 17. Спасибо за внимание!
Алгебра Алгебра - раздел математики, который можно грубо охарактеризовать как обобщение и расширение арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем.
Слайд 2Алгебра
Алгебра - раздел математики, который можно грубо охарактеризовать как обобщение и расширение
арифметики. Слово «алгебра» также употребляется в названиях различных алгебраических систем.
Слайд 3Геометрия
Геометрия-раздел математики, изучающий пространственные структуры и отношения, а также их обобщения. Геометрия как систематическая наука
появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.
Слайд 4Основные формулы в алгебре
Степень с натуральным показателем.
Степень с целым
показателем.
Формулы сокращенного умножения (ФСУ).
Решение неполных квадратных уравнений.
Слайд 5Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аn.
Действие, посредством которого находится
произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аn – степень, а – основание степени, n – показатель степени.
а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
а1=а Любое число в первой степени равно самому себе.
am∙an=am+n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
am:an=am— n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(am)n=amn При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)n=an∙bn При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)n=an/bn При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.
а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
а1=а Любое число в первой степени равно самому себе.
am∙an=am+n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
am:an=am— n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
(am)n=amn При возведении степени в степень основание оставляют прежним, а показатели перемножают
(a∙b)n=an∙bn При возведении произведения в степень возводят в эту степень каждый из множителей.
(a/b)n=an/bn При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.
Степень с натуральным показателем.
Слайд 6Степень с целым показателем.
(- n)-й степенью (n – натуральное) числа а, не равного
нулю, считается число, обратное n-й степени числа а, т.е. a— n=1/an. (10-2=1/102=1/100=0,01).
(a/b)— n=(b/a)n
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
(a/b)— n=(b/a)n
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Слайд 7Формулы сокращенного умножения (ФСУ).
(a+b)2=a2+2ab+b2 Квадрат суммы двух выражений равен квадрату первого выражения плюс
удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2=a2-2ab+b2 Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
a2-b2=(a-b)(a+b) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
(a+b)3=a3+3a2b+3ab2+b3 Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a-b)3= a3-3a2b+3ab2-b3 Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
a3+b3=(a+b)(a2-ab+b2) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3-b3=(a-b)(a2+ab+b2) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc Квадрат суммы трех выражений равен сумме квадратов этих выражений плюс всевозможные удвоенные попарные произведения самих выражений.
Справка. Полный квадрат суммы двух выражений: a2 + 2ab + b2
Неполный квадрат суммы двух выражений: a2 + ab + b2
(a-b)2=a2-2ab+b2 Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
a2-b2=(a-b)(a+b) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
(a+b)3=a3+3a2b+3ab2+b3 Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a-b)3= a3-3a2b+3ab2-b3 Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
a3+b3=(a+b)(a2-ab+b2) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3-b3=(a-b)(a2+ab+b2) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
(a+b+c)2=a2+b2+c2+2ab+2ac+2bc Квадрат суммы трех выражений равен сумме квадратов этих выражений плюс всевозможные удвоенные попарные произведения самих выражений.
Справка. Полный квадрат суммы двух выражений: a2 + 2ab + b2
Неполный квадрат суммы двух выражений: a2 + ab + b2
Слайд 8Решение неполных квадратных уравнений.
ax2=0 – неполное квадратное уравнение (b=0, c=0). Решение: х=0. Ответ: 0.
ax2+bx=0 – неполное квадратное уравнение (с=0). Решение:
x (ax+b)=0 → x1=0 или ax+b=0 → x2=-b/a. Ответ: 0; -b/a.
ax2+c=0 – неполное квадратное уравнение (b=0); Решение: ax2=-c → x2=-c/a.
Если (-c/a)<0, то действительных корней нет. Если (-с/а)>0, то имеем два действительных корня:
ax2+c=0 – неполное квадратное уравнение (b=0); Решение: ax2=-c → x2=-c/a.
Если (-c/a)<0, то действительных корней нет. Если (-с/а)>0, то имеем два действительных корня:
Слайд 9Решение полных квадратных уравнений.
ax2+bx+c=0 – квадратное уравнение общего вида
Дискриминант D=b2— 4ac.
Если D>0, то имеем два
действительных корня:
Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).
Если D<0, то действительных корней нет.
ax2+bx+c=0 – квадратное уравнение частного вида при четном втором
коэффициенте b
Если D=0, то имеем единственный корень (или два равных корня) х=-b/(2a).
Если D<0, то действительных корней нет.
ax2+bx+c=0 – квадратное уравнение частного вида при четном втором
коэффициенте b
Слайд 10Основные формулы в геометрии
Теорема Пифагора.
Площадь параллелограмма.
Значения синуса, косинуса, тангенса,
котангенса
Таблица Брадиса
Теорема Фалеса
Слайд 11Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c²=a²+b².
Слайд 12Признаки параллелограмма.
Если две противоположные стороны четырехугольника параллельны и равны, то этот
четырехугольник — параллелограмм.
Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.
Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Слайд 14Значения синуса, косинуса, тангенса, котангенса
Синусом угла α называется отношение длин противолежащего катета
к гипотенузе.
Косинусом угла α называется отношение длин прилежащего катета к гипотенузе.
Тангенсом угла α называется отношение длин противолежащего катета к прилежащему.
Котангенсом угла α называется отношение длин прилежащего катета к противолежащему.
Слайд 16Теорема Фалеса
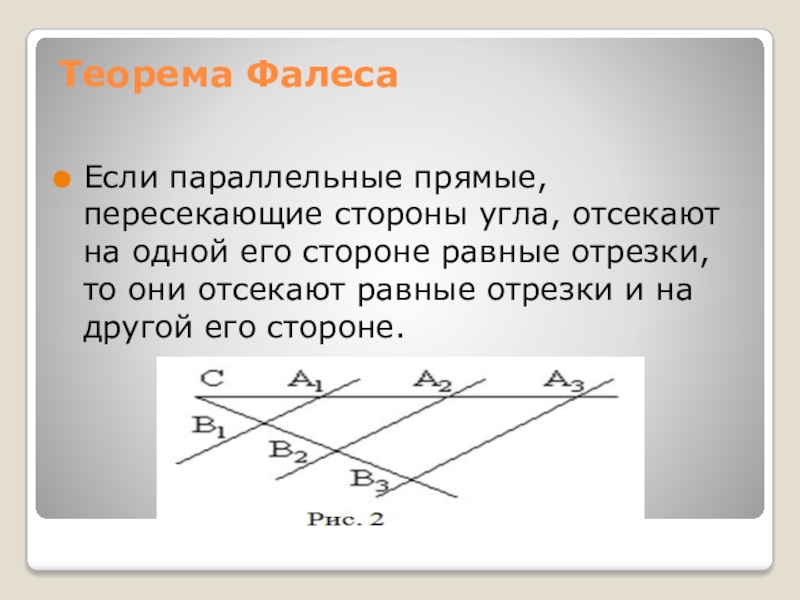
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его
стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.