- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Начальные геометрические сведения. Прямая и отрезок (7 класс)
Содержание
- 1. Презентация по геометрии Начальные геометрические сведения. Прямая и отрезок (7 класс)
- 2. Что это такое геометрия? Для чего она
- 3. При строительстве египетских пирамид использовались накопленные с
- 4. Итак, в геометрии изучаются форма, размеры и взаимное
- 5. Для чего нужна геометрия, мы частично ответили:
- 6. Школьный курс геометрии состоит из двух частей-планиметрии
- 7. Какая из фигур называется: прямоугольник, квадрат, круг,
- 8. Прямая – это бесконечная линия на плоскости.Прямая
- 9. Часть прямой ограниченная точками, называется ОТРЕЗКОМ. Точки
- 10. Точки D, B, C, T - не
- 11. Задание:Начертите прямую ВС. Отметьте точки, лежащие на
- 12. Отметьте в тетради точку А и точку
- 13. РАССМОТРИМ ТЕПЕРЬ ДВЕ ПРЯМЫЕЕсли две прямые имеют
- 14. Задания для закрепления:№2, 5, 6 в учебнике.Д.З. параграф 1,2, вопросы 1-3.
Что это такое геометрия? Для чего она нужна? Кратко можно сказать так: геометрия нужна для описания формы предметов, определения из размеров и взаимного расположения. Геометрия возникла очень давно, более 4000 лет назад. Само слово
Слайд 2Что это такое геометрия? Для чего она нужна? Кратко можно сказать
так: геометрия нужна для описания формы предметов, определения из размеров и взаимного расположения.
Геометрия возникла очень давно, более 4000 лет назад. Само слово «геометрия» в переводе с греческого означает «землемерие» (по-гречески «гео» – земля, а «метрео» – мерить). Это название объясняется тем, что возникновение геометрии было связано с практической деятельностью – разметкой земельных участков, прокладыванием дорог, строительством сложных архитектурных сооружений (например, египетских пирамид). С развитием мореплавания появилась потребность ориентироваться по звездам и составлять географические карты. Так возникла еще одна из задач геометрии – задача об изучении взаимного расположения геометрических фигур.
Слайд 3При строительстве египетских пирамид использовались накопленные с глубокой древности практические геометрические
правила.
Слайд 4Итак, в геометрии изучаются форма, размеры и взаимное расположение геометрических фигур. На первых
порах развития геометрии появлялись и постепенно накапливались правила, связанные с геометрическими измерениями и построениями. Но затем благодаря древнегреческим ученым (Фалесу, Пифагору, Евклиду и др.) все большую роль в геометрии стали играть рассуждения, позволяющие выводить новые формулы и неизвестные ранее факты из уже известных. К началу нашей эры геометрия сформировалась как наука, в которой свойства геометрических фигур изучаются с помощью рассуждений.
Слайд 5Для чего нужна геометрия, мы частично ответили: есть много практических задач,
которые решаются с ее помощью. Но это еще не все. Обосновывая справедливость каких-то утверждений, доказывая их, мы учимся рассуждать, а это важно в любом деле. Геометрия поражает воображение тем, что путем рассуждений в ней порой устанавливаются совершенно неожиданные факты. Неудивительно, что на протяжении многих веков люди самых разнообразных профессий посвящали часы досуга занятиям геометрией.
Слайд 6Школьный курс геометрии состоит из двух частей-планиметрии и стереометрии. В планиметрии
рассматриваются плоские фигуры — прямоугольники, отрезки, треугольники, окружности, четырехугольники и т.д.,
В стереометрии рассматриваются пространственные фигуры, например, параллелепипеды, шары, цилиндры(рис. 5).
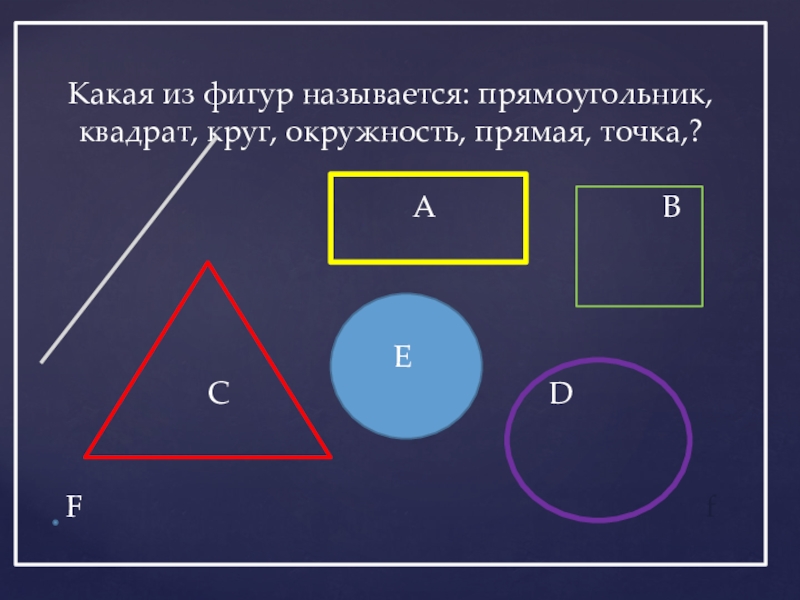
Слайд 7Какая из фигур называется: прямоугольник, квадрат, круг, окружность, прямая, точка,?
А В
E
C D
F f
Слайд 8Прямая – это бесконечная линия на плоскости.
Прямая обозначается двумя заглавными буквами
(например АВ или ВА) или одной строчной буквой (например - а)
А В
а
А В
а
Прямая и отрезок
Слайд 9Часть прямой ограниченная точками, называется ОТРЕЗКОМ. Точки – называются КОНЦАМИ ОТРЕЗКА.
Отрезок называют по его концам.
На рисунке изображен отрезок АВ или ВА.
А В
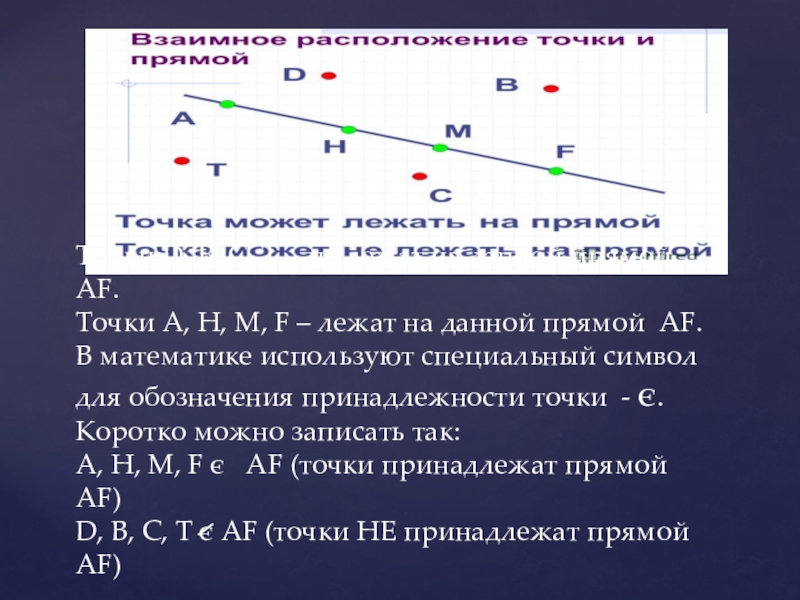
Слайд 10Точки D, B, C, T - не лежат на данной прямой
АF.
Точки А, Н, М, F – лежат на данной прямой AF.
В математике используют специальный символ для обозначения принадлежности точки - є.
Коротко можно записать так:
А, Н, М, F є AF (точки принадлежат прямой AF)
D, B, C, T є AF (точки НЕ принадлежат прямой AF)
Слайд 11Задание:
Начертите прямую ВС. Отметьте точки, лежащие на этой прямой – А,
М, Н. Отметьте точки, не лежащие на прямой – О, Р , Х.
Обозначьте принадлежность точек новым символом є
Обозначьте принадлежность точек новым символом є
Слайд 12Отметьте в тетради точку А и точку В. проведите через них
прямую. Можно ли через эти же точку провести еще одну прямую, отличную, от проведенной ранее?
Выполняйте рисунок!
Можно ли через эти же точку провести еще одну прямую, отличную, от проведенной ранее?
Нет. Потому что ЧЕРЕЗ ЛЮБЫЕ ДВЕ ТОЧКИ МОЖНО ПРОВЕСТИ ПРЯМУЮ И ПРИТОМ ТОЛЬКО ОДНУ.
Данное утверждение является СВОЙСТВОМ ПРЯМОЙ.
Выполняйте рисунок!
Можно ли через эти же точку провести еще одну прямую, отличную, от проведенной ранее?
Нет. Потому что ЧЕРЕЗ ЛЮБЫЕ ДВЕ ТОЧКИ МОЖНО ПРОВЕСТИ ПРЯМУЮ И ПРИТОМ ТОЛЬКО ОДНУ.
Данное утверждение является СВОЙСТВОМ ПРЯМОЙ.
Слайд 13РАССМОТРИМ ТЕПЕРЬ ДВЕ ПРЯМЫЕ
Если две прямые имеют общую точку, то говорят,
что они ПЕРЕСЕКАЮТСЯ.
Две прямые могут иметь лишь ОДНУ ОБЩУЮ ТОЧКУ, либо не иметь общих точек вообще.
Пересечение прямых имеет свое обозначение с помощью символа: а Х в (прямая а пересекается с прямой в). Прямые пересекаются в точке О.
а О
Две прямые могут иметь лишь ОДНУ ОБЩУЮ ТОЧКУ, либо не иметь общих точек вообще.
Пересечение прямых имеет свое обозначение с помощью символа: а Х в (прямая а пересекается с прямой в). Прямые пересекаются в точке О.
а О
в