- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Векторы и их применение
Содержание
- 1. Презентация по теме Векторы и их применение
- 2. Содержание1.Понятие вектора2.Коллинеарные векторы3.Равенство векторов4.Откладывание вектора от данной
- 3. Понятие вектораРассмотрим произвольный отрезок. На нем можно
- 4. Любая точка плоскости также является вектором, который
- 5. Длиной или модулем ненулевого вектора АВ называется
- 6. Коллинеарные векторыНенулевые векторы называются коллинеарными, если они
- 7. Равенство векторовОпределение. Векторы называются равными,
- 8. Откладывание вектора от данной точкиЕсли точка А
- 9. Сумма двух векторовПравило треугольника Пусть а
- 10. Законы сложения векторов1) а+b=b+a (переместительный закон) Правило
- 11. Сумма нескольких векторовПравило многоугольникаs=a+b+c+d+e+f k+n+m+r+p=0 abcdefskmnrpO
- 12. Противоположные векторы Пусть
- 13. Вычитание векторов Определение.
- 14. Умножение вектора на число
- 15. Для любых чисел k, n и любых
- 16. Скалярное произведение векторов.Скалярным произведением двух векторов называетсяпроизведение их длинна косинус угла междуними.
- 17. Если , то Если, тоЕсли, тоЕсли, тоСкалярное произведениеназываетсяскалярным квадратом вектора
- 18. Свойства скалярного произведения - переместительное свойство- сочетательное
- 19. Немного об историиИстоки векторного исчисления находятся в
- 20. Учёные Европы Симон Стевин (1548 - 1620)
- 21. Говорил о строение геометрического исчисления, изучающего направление
- 22. ПРИМЕНЕНИЕ ВЕКТОРОВПРЯМОЕ ЗНАЧЕНИЕПЕРЕНОСНОЕ ЗНАЧЕНИЕМатематикаФизикаФизкультураСилаРавноускоренное движениеРавномерноедвижениеЭстафетыВолейболБаскетболКартографияНавигацияТехника
- 23. ДВИЖЕНИЕ
- 24. ЭСТАФЕТА
- 25. БАСКЕТБОЛАмериканские профессиональные баскетболисты показывали удивительное зрелище: игру в темноте светящимся мячом. Видна была только траектория мяча.
- 26. КартографияВ картографии, для управления географическими данными используются
- 27. Биоакустика изучаетсигналы биообъектов втолще океанов и морей.Решает
- 28. ТехникаНовая векторная технология управления телевизор. Новая концепция
- 29. Сейсмоакустика.Сейсмоакустика - регистрацию сигналов от слабых источников,
- 30. Лучевая скоростьНАВИГАЦИЯ - раздел науки оспособах проведенияморских,
- 31. Лучевая скорость - проекция скорости звезды в
- 32. Задача №1 Дан произвольный треугольник АВС.
- 33. №2 Дано: куб
- 34. Тест:Вставьте пропущенное слово:Скалярным произведением двух векторов называется
- 35. Какие из представленных на рисунке векторов перпендикулярны?О
- 36. Сопоставьте углы между векторами и их градусной
- 37. Выберите правильный ответ;Известно, что Скалярное произведениевекторов равно: а)б)в)
- 38. Ответ: а21 способ:
- 39. Ответ: а22 способ:
- 40. Введем прямоугольную систему координат.хуzОтвет: а23 способ:
- 41. РешениеОбозначим медианы треугольника АВС через ВЕ, СF
Слайд 2Содержание
1.Понятие вектора
2.Коллинеарные векторы
3.Равенство векторов
4.Откладывание вектора от данной точки
5.Сумма двух векторов
6.Законы сложения
7.Сумма нескольких векторов
8.Противоположные векторы
9.Вычитание векторов
10.Умножение вектора на число
11.Скалярное произведение векторов
12.Свойства скалярного произведения
13.Немного об истории
14.Применение векторов
15.Задачи
16.Тест
Слайд 3Понятие вектора
Рассмотрим произвольный отрезок. На нем можно указать два направления.
Определение.
Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.
Слайд 4
Любая точка плоскости также является вектором, который называется НУЛЕВЫМ. Начало нулевого
ММ = 0.
М
Слайд 5Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ:
с = 17
Длина нулевого вектора считается равной нулю:
ММ = 0.
a
М
В
А
с
Слайд 6Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если они лежат либо на одной
Нулевой вектор считается коллинеарным любому вектору.
а
b
c
d
m
n
s
L
Слайд 7Равенство векторов
Определение.
Векторы называются равными, если они сонаправлены и
а = b , если
а b
а = b
а
c
b
d
m
n
s
f
Слайд 8Откладывание вектора от данной точки
Если точка А – начало вектора а
Утверждение: От любой точки М можно отложить вектор, равный данному вектору а, и притом только один.
Равные векторы, отложенные от разных точек, часто обозначают одной и той же буквой
А
а
М
а
Слайд 9Сумма двух векторов
Правило треугольника
Пусть а и b – два
АС = а + b
a
b
A
a
b
B
C
Слайд 10Законы сложения векторов
1) а+b=b+a (переместительный закон) Правило параллелограмма
Пусть а
АС = АВ + BС = а+b
АС = АD + DС = b+a
2) (а+b)+c=a+(b+c)
(сочетательный закон)
a
a
b
b
A
D
C
B
a
b
Слайд 12Противоположные векторы
Пусть а – произвольный ненулевой
Определение. Вектор b называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены.
a = АВ, b = BA
Вектор, противоположный вектору c, обозначается так: -c.
Очевидно, с+(-с)=0 или АВ+ВА=0
А
B
a
b
c
-c
Слайд 13Вычитание векторов
Определение. Разностью двух векторов а
Теорема. Для любых векторов а и b справедливо равенство а - b = а + (-b).
Задача. Даны векторы а и b. Построить вектор а – b.
а
а
b
-b
-b
a - b
Слайд 14Умножение
вектора на число
Определение. Произведением ненулевого
противоположно направлены при k<0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора а векторы а и ka коллинеарны.
а
-2a
3а
Слайд 15 Для любых чисел k, n и любых векторов а, b справедливы
(kn) а = k (na) (сочетательный закон)
(k+n) а = kа + na (первый распределительный закон)
K ( а+ b ) = kа + kb (второй распределительный закон)
Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например,
p = 2( a – b) + ( c + a ) – 3( b – c + a ) =
= 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c
Слайд 16Скалярное произведение векторов.
Скалярным произведением
двух векторов называется
произведение их длин
на косинус угла
ними.
Слайд 17
Если , то
Если
, то
Если
,
Если
, то
Скалярное произведение
называется
скалярным квадратом вектора
Слайд 18Свойства скалярного произведения
- переместительное свойство
- сочетательное свойство
распределительное
Слайд 19Немного об истории
Истоки векторного исчисления находятся в механике и астрономии, где
Архимед в работе «О спиралях» использовал правило параллелограмма а позже и Птолемей в своём знаменитом «Альмагесте». Астрономы средневекового Восток, развивая теорию Птолемея, постоянно использовали «сложение движений».
Аристо́тель (384 до н. э.)
Архиме́д (287 год до н. э. — 212 год до н. э.)
Кла́вдий Птолеме́й. В период с 127 по 151 год жил в Александрии, где проводил астрономические наблюдения
Слайд 20Учёные Европы Симон Стевин (1548 - 1620) - в «Основах статистики»
сложения направленных отрезков, которыми они изображали силы, скорости, ускорения
Си́мон Сте́вин (1548—1620)
Джон Валлис
в 1845 г. в работе «О геометрических суммах и разностях и их применении для упрощения изложения механики» разработал теорию сложения и вычитания направленных отрезков.
Адемар Жан-Клод Барре Сен-Венан.1797 —1886
Слайд 21Говорил о строение геометрического исчисления, изучающего направление отрезки, их длину, углы
Готфрид Вильгельм фон Лейбниц
(1646—1716)
В книге «Геометрия положения» исследовал направленные отрезки и углы между ними. Он ввёл обозначение АВ для отрезка с началом в точке А и концом в точке В
Лаза́р Карно́
(1753-1823)
В 1844 г. в первой публикации по теории кватернионов Гамильтон ввел термин «вектор», образовав его от латинского слова «vehere» - «нести». Он писал: «Шаг от точки А к точки В можно рассматривать как работу по транспортировки или переносу подвижной точки из начального положения в конечное».
Уильям Роуэн Гамильтон
Слайд 22
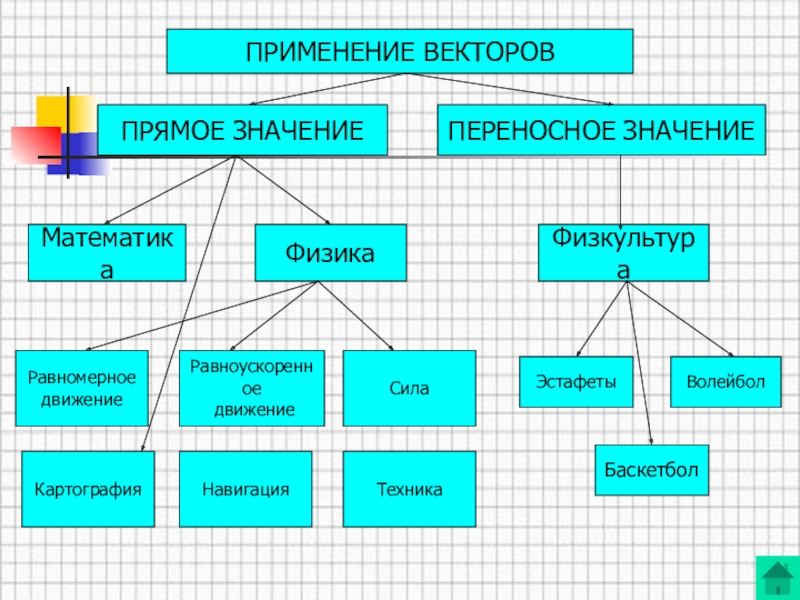
ПРИМЕНЕНИЕ ВЕКТОРОВ
ПРЯМОЕ ЗНАЧЕНИЕ
ПЕРЕНОСНОЕ ЗНАЧЕНИЕ
Математика
Физика
Физкультура
Сила
Равноускоренное
движение
Равномерное
движение
Эстафеты
Волейбол
Баскетбол
Картография
Навигация
Техника
Слайд 25БАСКЕТБОЛ
Американские профессиональные баскетболисты показывали удивительное зрелище: игру в темноте светящимся мячом.
Слайд 26Картография
В картографии, для управления географическими данными используются векторные карты.
Векторные карты состоят
При планировании городских микрорайонов и построении новых жилых домов учитываются многие факторы, в том числе доминирующие направления ветра. Векторное поле скорости движения воздуха в окрестности здания.
Слайд 27Биоакустика изучает
сигналы биообъектов в
толще океанов и морей.
Решает вопросы дальнего
И сверхдальнего
распространения сигналов
в
Распределение температуры воздуха представлено полупрозрачной тоновой заливкой в вертикальной плоскости сечения (цветами, а не привычными стрелочками), что позволяет видеть интерьер салона.
Распределение температуры воздуха в салоне автомобиля.
Внешний вид первого векторного гидроакустический приемник
Слайд 28Техника
Новая векторная технология управления телевизор. Новая концепция способна революционизировать сравнительно непростую
Слайд 29Сейсмоакустика.
Сейсмоакустика - регистрацию сигналов от слабых источников, в том числе подрывов,
Пример совместной обработки сигналов при выстреле гаубицы, регистрируемых каналами Х, Y и Z векторного приемника, расположенного в воздухе
Круг решаемых задач, в которых в той или иной мере используется информация о векторных характеристиках полей, гораздо шире, чем собственно проблемы гидро- и сейсмоакустики. В частности,
– изучение характеристик звуковых полей в замкнутых объемах представляет важную проблему, являющуюся основой решения задач архитектурной акустики и экологии, обеспечивающих необходимое качество восприятия звука в закрытых помещениях и защиты человека от вредного физиологического воздействия звука.
– вопросы качества восприятия звука
– биофизические задачи.
Слайд 30Лучевая скорость
НАВИГАЦИЯ - раздел науки о
способах проведения
морских, воздушных судов и
космических летательных
аппаратов
пространства в другую.
Астрономические методы
навигации основаны на
определении положения
известных небесных светил
относительно выбранной
системы координат
Лучевая скорость— это скорость, с которой тело приближается к наблюдателю или удаляется от него. Эту скорость можно представить как проекцию вектора полной скорости тела относительно наблюдателя на луч зрения, т. е. на прямую линию, соединяющую его с наблюдателем.
Слайд 31Лучевая скорость - проекция скорости звезды в пространстве.
Лучевую скорость небесных
Эффект Доплера имеет важное значение в астрономии, гидролокации и радиолокации. В астрономии по доплеровскому сдвигу определенной частоты испускаемого света можно судить о скорости движения звезды вдоль линии ее наблюдения. используется для определения скорости движения подводных лодок
Слайд 32Задача
№1
Дан произвольный треугольник АВС. Доказать, что можно построить треугольник,
Решение.
Слайд 33
№2
Дано: куб АВСDA1B1C1D1;
АВ
Найти:
Решение:
1 способ
2 способ
3 способ
Слайд 34Тест:
Вставьте пропущенное слово:
Скалярным произведением двух векторов называется число, равное произведению модулей
косинус
Слайд 35Какие из представленных на рисунке векторов перпендикулярны?
О
а и c
2. b и d
3. с и d
b и с
f и d
Слайд 36Сопоставьте углы между векторами и их градусной мерой.
О
c и f
d и a 45 o
a и f 180 o
a и b 135 o
450
Слайд 41Решение
Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие
ВС = а, СА = в, АВ = с
Тогда
АD = АВ + ВD = АВ += с + аналогично определяются и другие медианы:
ВЕ = а + , СF = в + Так как, в силу условия замкнутости
ВС + СА + АВ = а + в + с =0,
то мы имеем:
АD + ВЕ + СF = ( с + ) + (а + ) + ( в + ) = ( а + в + с) = х 0 = 0.
Следовательно, отложив от точки В, вектор В1С1 = ВЕ и от точки С1 – вектор С1D1 = СF, мы получим.
А1В1 + В1С1 + С1D1 = АD + ВЕ + СF = 0.
А это значит (в силу условия замкнутости), что ломаная А1В1С1D1 является замкнутой, т.е. точка D1 совпадает с А1.
Таким образом, мы получаем треугольник А1В1С1 (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.