- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок в 8 классе: Теорема Пифагора
Содержание
- 1. Урок в 8 классе: Теорема Пифагора
- 2. Данный урок составлен для проведения в 8А
- 3. Цель урока: Расширить познания учащихся о жизни
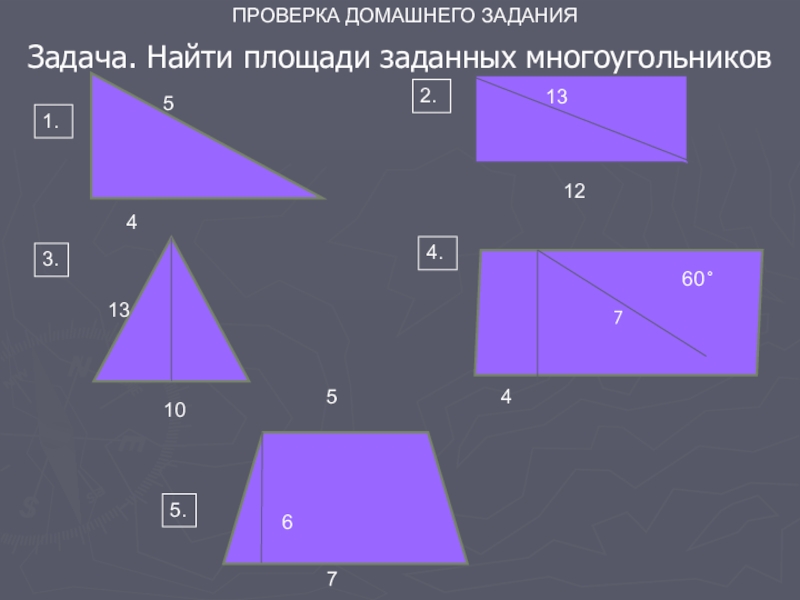
- 4. 41. 10102.Задача. Найти площади заданных многоугольников512131374.573.5.6460 ̊̊ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
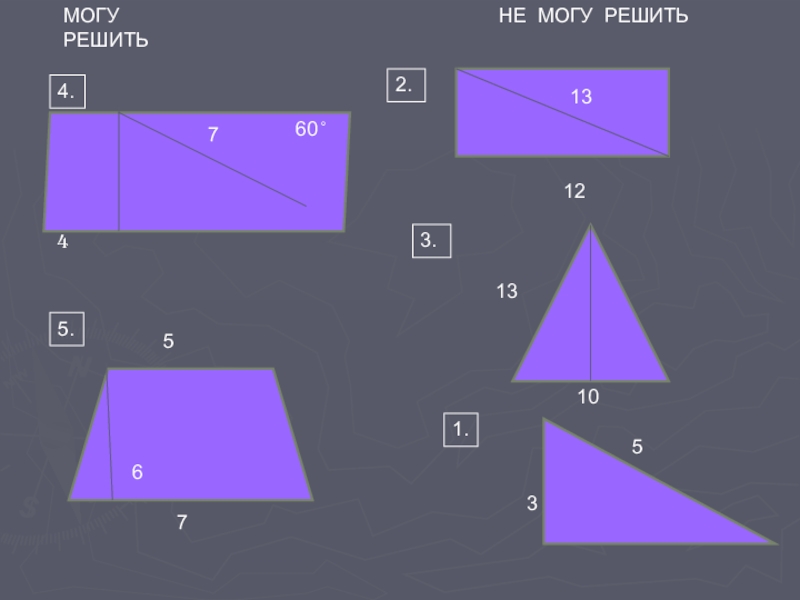
- 5. 4.410102.512131373.575.1.МОГУ РЕШИТЬНЕ МОГУ РЕШИТЬ3660 ̊
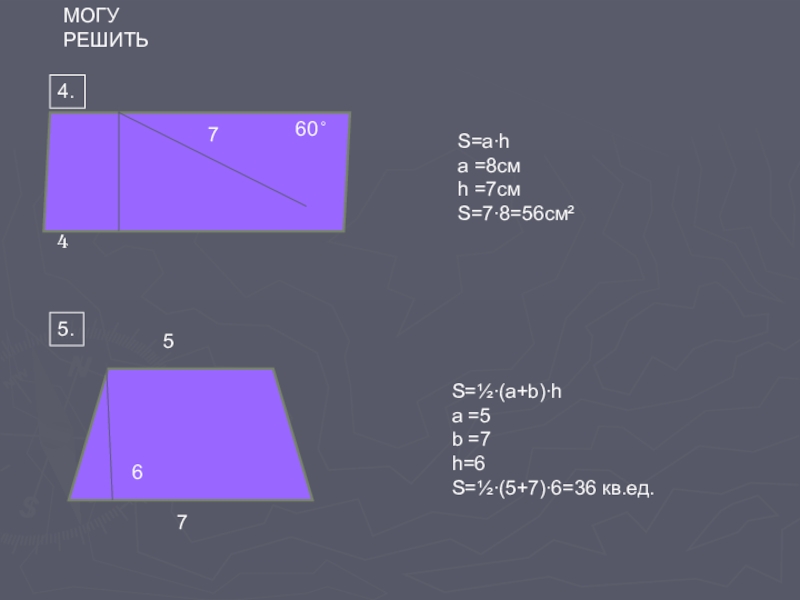
- 6. 4.47575.МОГУ РЕШИТЬ660 ̊S=a∙ha =8смh =7смS=7∙8=56cм²S=½∙(a+b)∙ha =5b =7h=6S=½∙(5+7)∙6=36 кв.ед.
- 7. 102.51213133.1.НЕ МОГУ РЕШИТЬ3 ???
- 8. Теорема Пифагора – одна из важнейших теорем
- 9. Пребудет вечной истина, как скоро Ее познает
- 10. Обозначения сторон прямоугольного треугольникаГипотенуза – сторона, лежащая
- 11. «В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 12. ТЕОРЕМА.В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 13. Простейшее доказательство
- 14. Если квадрат одной стороны треугольника, равен сумме
- 15. В чем же причина такой популярности «пифагоровых
- 16. Теорема Пифагора – одна из самых главных
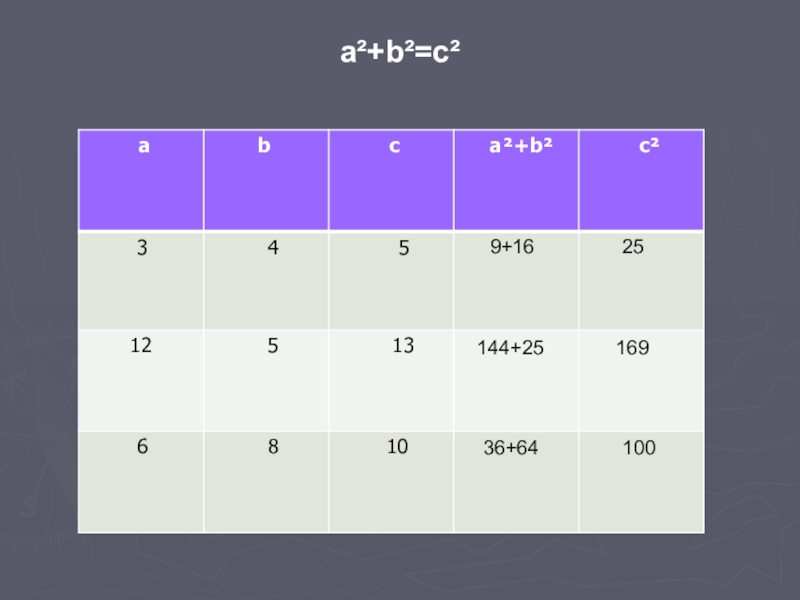
- 17. 9+1625144+2516936+64100a²+b²=c²
- 18. Прямоугольные треугольники с целочисленными сторонами называют египетскими,
- 19. Закрепление изученного материалаФОРМУЛЫ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ:
- 20. 102.51213133.1.
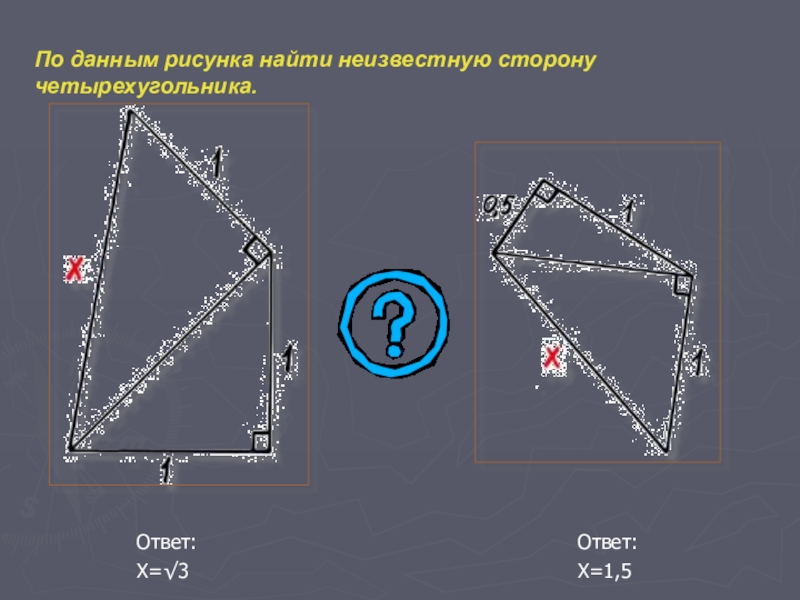
- 21. По данным рисунка найти неизвестную сторону четырехугольника.Ответ:Х=√3Ответ:Х=1,5
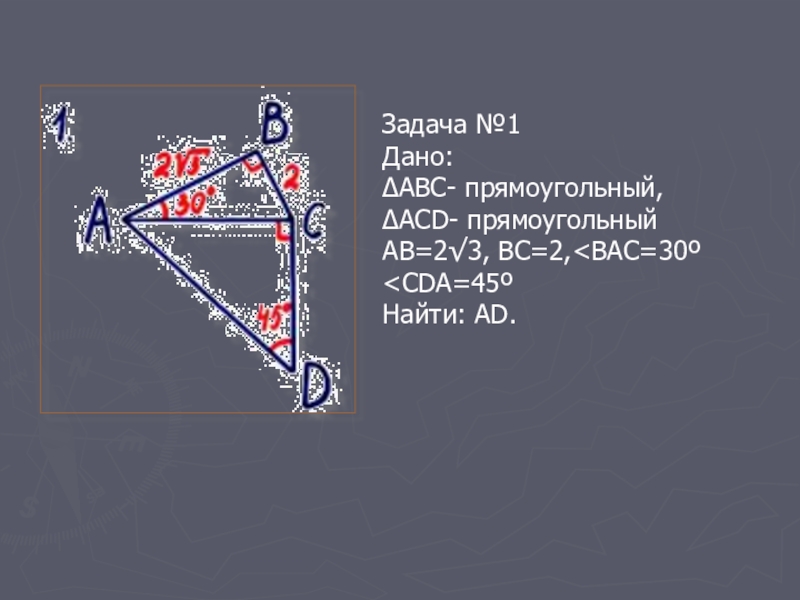
- 22. Задача №1Дано:∆АВС- прямоугольный,∆АСD- прямоугольныйАВ=2√3, ВС=2,
- 23. Решение:1.∆АВС- прямоугольный, зная что против угла в
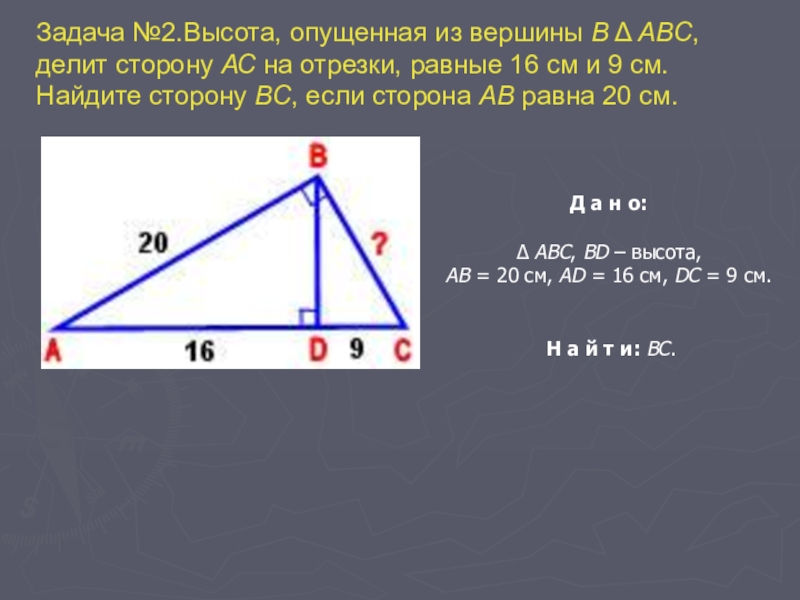
- 24. Задача №2.Высота, опущенная из вершины В Δ
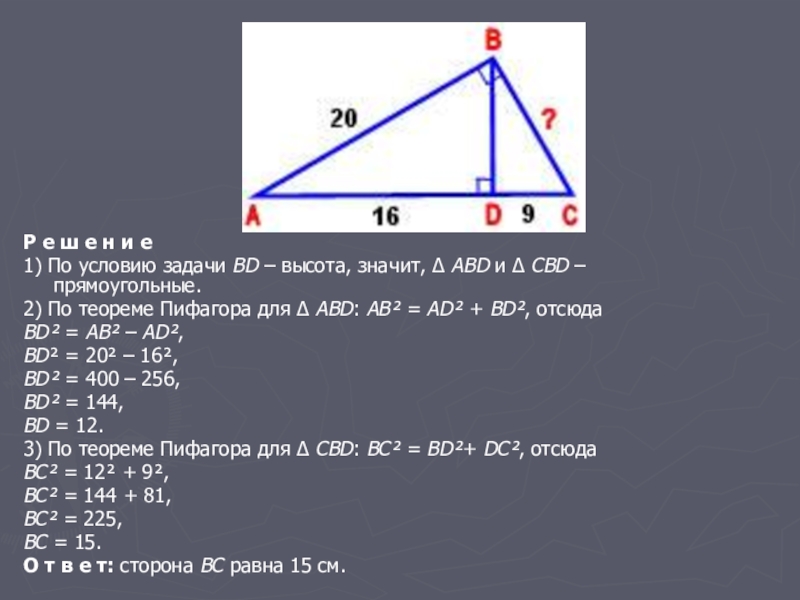
- 25. Р е ш е н и е 1) По условию задачи BD –
- 26. Задача №3. Найти площадь треугольника, стороны которого
- 27. Изречения Пифагора, актуальные и в наши дни:Не
- 28. № 483(а); 484(а, г).ДОМАШНЕЕ ЗАДАНИЕ: найти другие способы доказательства теоремы Пифагора.
- 29. СПАСИБО ЗАУРОК!!!СПАСИБО ЗАУРОК!!!
Слайд 1Электронное сопровождение к изучению темы:
«Теорема Пифагора»
Шулаева Елена Николаевна,
учитель математики
гимназии №3
г. Зеленодольска
Слайд 2Данный урок составлен для проведения в 8А классе.
8А класс- гимназический;
В классе
Математика-5 часов в неделю;
Достижения прошлого учебного года:
1 и 2 место в городской олимпиаде по математике.
1 место в городских Лобачевских чтениях
Слайд 3Цель урока:
Расширить познания учащихся о жизни великого Пифагора. Доказать теорему
Задачи урока:
научить
-пользоваться формулой a²+b²=c²
-видеть необходимость применения, изученных теорем при решении задач.
Теорема
Пифагора
Слайд 4
4
1.
10
10
2.
Задача. Найти площади заданных многоугольников
5
12
13
13
7
4.
5
7
3.
5.
6
4
60 ̊̊
ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
Слайд 64.
4
7
5
7
5.
МОГУ РЕШИТЬ
6
60 ̊
S=a∙h
a =8см
h =7см
S=7∙8=56cм²
S=½∙(a+b)∙h
a =5
b =7
h=6
S=½∙(5+7)∙6=36 кв.ед.
Слайд 8Теорема Пифагора –
одна из важнейших
теорем геометрии. О ней знает
Эта теорема позволяет значительно расширить круг задач, решаемых в курсе геометрии.
Пифагор Самосский(580-500г до н. э.)
Древнегреческий философ,
религиозный и политический деятель, математик.
Слайд 9 Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Сонет немецкого писателя-романиста
А Шамиссо (начало XIX в.).
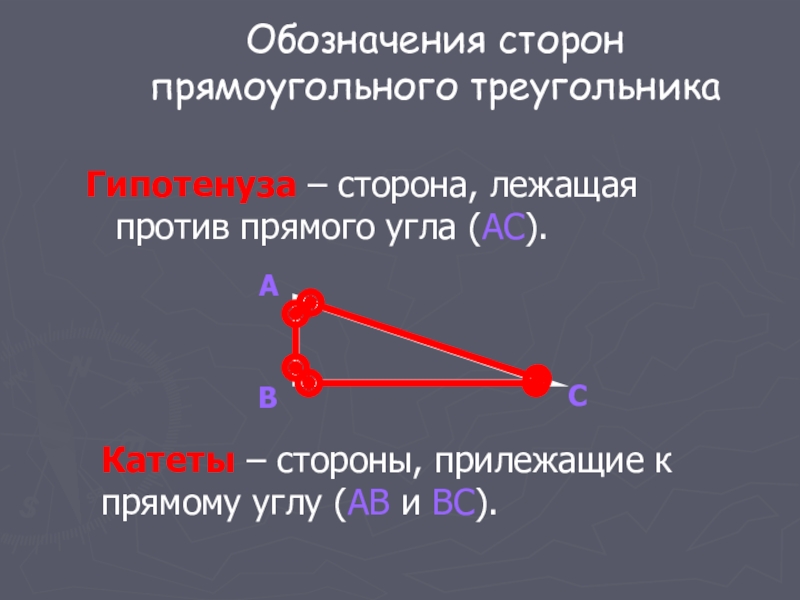
Слайд 10Обозначения сторон прямоугольного треугольника
Гипотенуза – сторона, лежащая против прямого угла (AC).
Катеты
A
B
C
Слайд 11
«В прямоугольном
треугольнике квадрат
гипотенузы равен
сумме квадратов
катетовкатетов».
Формулировки
Во времена Пифагора формулировка теоремы звучала так:
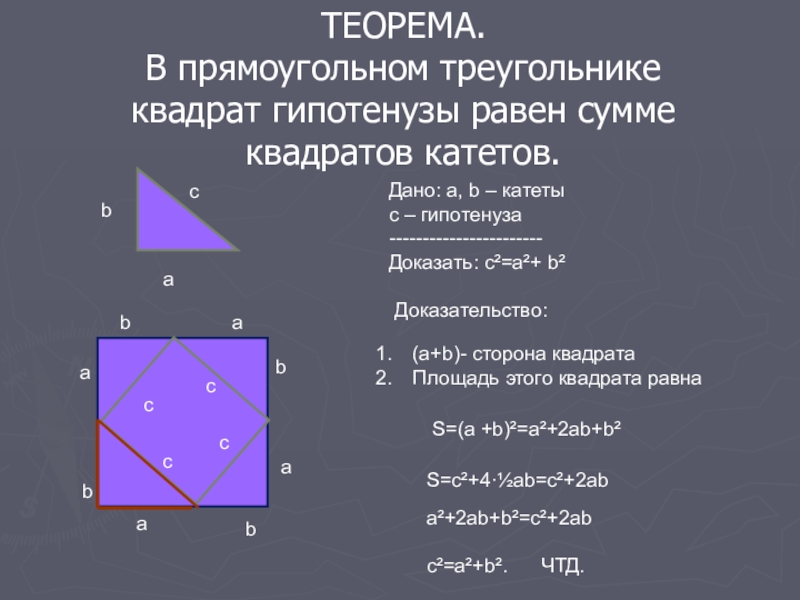
Слайд 12ТЕОРЕМА.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Доказательство:
а
а
а
b
b
b
b
(а+b)- сторона квадрата
Площадь
S=(a +b)²=a²+2ab+b²
S=c²+4∙½ab=с²+2аb
a²+2ab+b²=c²+2ab
c²=a²+b². ЧТД.
с
с
с
с
а
a
b
c
Дано: а, b – катеты
с – гипотенуза
-----------------------
Доказать: c²=a²+ b²
Слайд 14Если квадрат одной стороны треугольника, равен сумме квадратов двух других его
Дано: ∆АВС
АВ²=АС²+ВС²
Доказать: ∆АВС-прямоугольный.
Доказательство:
1.Рассмотрим прямоугольный
∆КМР, у которого КМ=АС,
МР=ВС.
2.По теореме Пифагора КМ²+МР²=КР²,
то АС²+ВС² =КР², но
АС²+ВС²=АВ²,следовательно
КР² =АВ², КР=АВ.
3. ∆АВС=∆КМР по 3 сторонам, то <С=90º, ∆АВС- прямоугольный.
ЧТД.
А
С
В
М
Р
К
Обратная теорема Пифагора:
Слайд 15
В чем же причина такой популярности
«пифагоровых штанов»?
б) простота,
а) красота,
в) значимость.
Знатоки утверждают, что причин здесь три:
Слайд 16Теорема Пифагора – одна из самых главных теорем геометрии. Из нее
Слайд 18Прямоугольные треугольники с целочисленными сторонами называют египетскими, а тройки целых чисел,
На прошлом слайде мы видели следующие тройки чисел:
3, 4, 5
5, 12, 13
6,8,10.
Они образуют пифагоровы тройки, прямоугольные треугольники с такими сторонами, являются египетскими треугольниками.
Слайд 19Закрепление изученного материала
ФОРМУЛЫ, НЕОБХОДИМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ:
c²=a²+b²
с=√ a²+b² a=√ c²-b² b=√ c²-b²
Слайд 20
10
2.
5
12
13
13
3.
1.
3
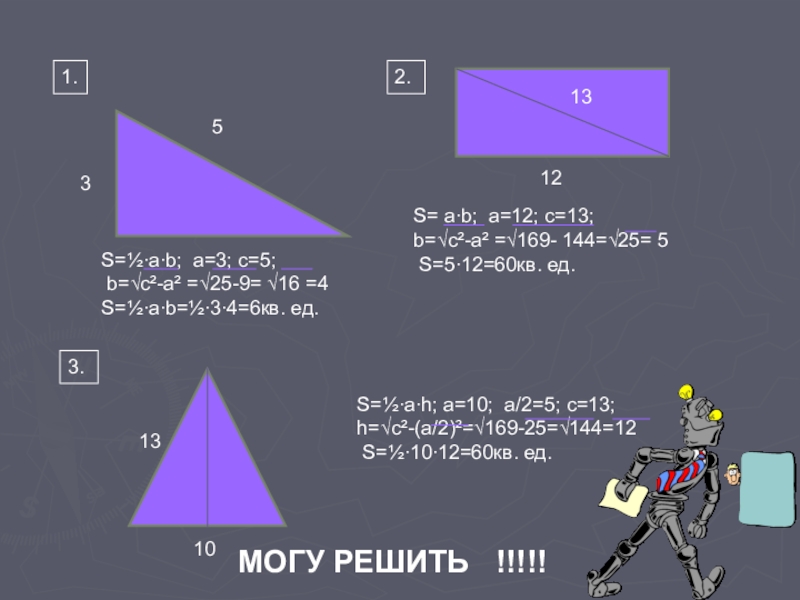
S=½∙a∙b; a=3; c=5;
b=√c²-a² =√25-9= √16 =4
S=½∙a∙b=½∙3∙4=6кв. ед.
S= a∙b; a=12; c=13;
b=√c²-a² =√169- 144=√25= 5
S=5∙12=60кв. ед.
S=½∙a∙h; a=10; a/2=5; c=13;
h=√c²-(a/2)²=√169-25=√144=12
S=½∙10∙12=60кв. ед.
МОГУ РЕШИТЬ !!!!!
Слайд 23
Решение:
1.∆АВС- прямоугольный, зная что против угла в 30º лежит катет равный
ВС=½АС, АС=4.
2.∆АСD- прямоугольный и равносторонний, то по теореме Пифагора:
AD²=AC²+CD²,
АD²=16+16,
АD²=32,
АD=4√2,
Ответ:АD=4√2.
Слайд 24
Задача №2.Высота, опущенная из вершины В Δ АВС, делит сторону АС
Найдите сторону ВС, если сторона АВ равна 20 см.
Д а н о:
Δ АВС, BD – высота,
АВ = 20 см, AD = 16 см, DC = 9 см.
Н а й т и: ВС.
Слайд 25
Р е ш е н и е
1) По условию задачи BD – высота, значит, Δ ABD
2) По теореме Пифагора для Δ ABD: АВ² = AD² + BD², отсюда
BD² = AB² – AD²,
BD² = 20² – 16²,
BD² = 400 – 256,
BD² = 144,
BD = 12.
3) По теореме Пифагора для Δ СBD: ВС² = ВD²+ DС², отсюда
BC² = 12² + 9²,
BC² = 144 + 81,
BC² = 225,
BC = 15.
О т в е т: сторона BC равна 15 см.
Слайд 26Задача №3. Найти площадь треугольника, стороны которого равны 15 см, 20
Решение:
1. Изданных чисел можно составить равенство
15²+20²=25², то 225+400=625.
Это равенство верно , то есть выполняется обратная теорема Пифагора, следовательно данный треугольник является прямоугольным.
2. Для нахождения площади прямоугольного треугольника воспользуемся формулой:
S=½а۰в, то S=½۰15۰20=150 см².
Ответ: 150 см².
Слайд 27Изречения Пифагора, актуальные и в наши дни:
Не поднимай пыли на жизненном
Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.
Не делай никогда того, чего не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь.
Не закрывай глаза, когда хочется спать, не разобравши всех своих поступков в прошлый день.