:
«Конус»
учителя математики
ГБОУ СОШ №1056
Романенко Елены Алексеевны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Конус
Содержание
- 1. Презентация по геометрии на тему Конус
- 2. Нас окружает множество предметов
- 3. ВИДЫ КОНУСОВНАКЛОННЫЙКОНУСПРЯМОЙКОНУСУСЕЧЁННЫЙКОНУС
- 4. Конусом называется тело, ограниченное кругом (основание конуса),
- 5. Конус – тело вращенияКонус может быть получен вращением прямоугольного треугольника вокруг одного из катетов.
- 6. Так выглядит развертка конуса Развёрткой конуса
- 7. Боковая поверхность конуса – круговой сектор, радиус
- 8. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
- 9. Полная поверхность конуса Площадь полной поверхности конуса равна сумме площадей боковой поверхности и основания:
- 10. Задача Какова площадь поверхности
- 11. Для решения задачи надо измерить:
- 12. Задача Сколько квадратных метров
- 13. Решение: Sбок.= πRℓR=D:2 =
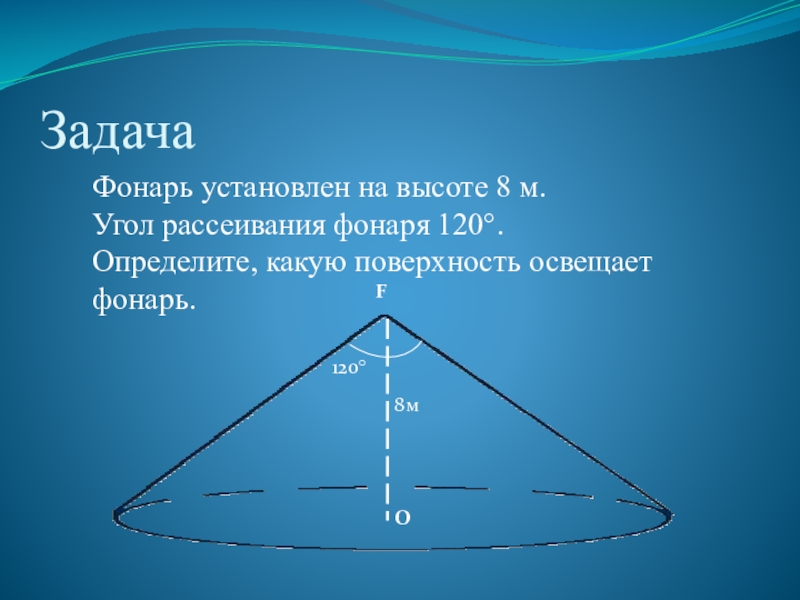
- 14. Задача FОФонарь установлен на высоте 8 м. Угол рассеивания фонаря 120°. Определите, какую поверхность освещает фонарь.120°8м
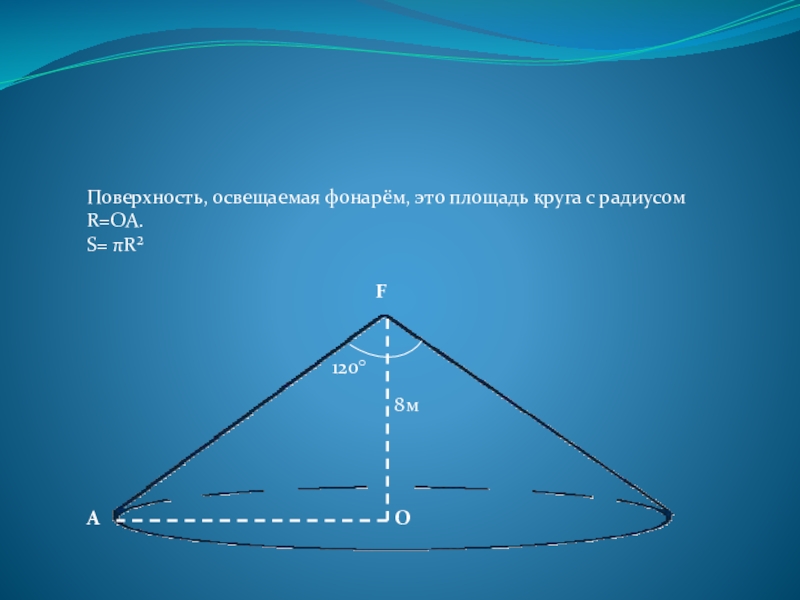
- 15. FОПоверхность, освещаемая фонарём, это площадь круга с радиусом R=ОА.S= πR²120°8мА
- 16. Решение: FАО= (180°-120°)/2=30° FA=8•2=16 (катет, лежащий
- 17. ЗадачаОбразующая конуса, равная 12 см, наклонена к
- 18. Задача Дано: конусl = 12 смα = 45°Найти:Sосн. = ?12 смАОВ45°Решение:Ответ: 72π см2.
- 19. Задача 5. Высота конуса равна 12, а
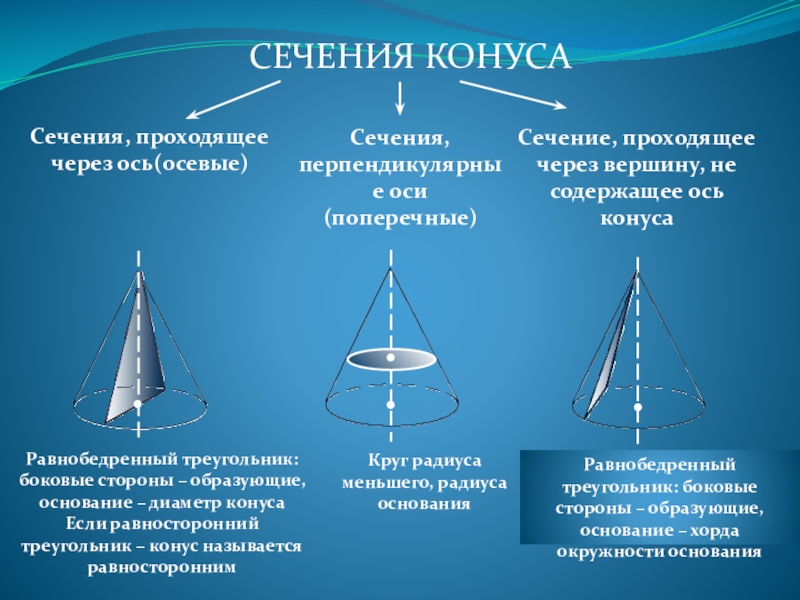
- 20. СЕЧЕНИЯ КОНУСАСечения, проходящее через ось(осевые)Сечения, перпендикулярные оси
- 21. Сечения конуса различными плоскостямиСекущая плоскость проходит через
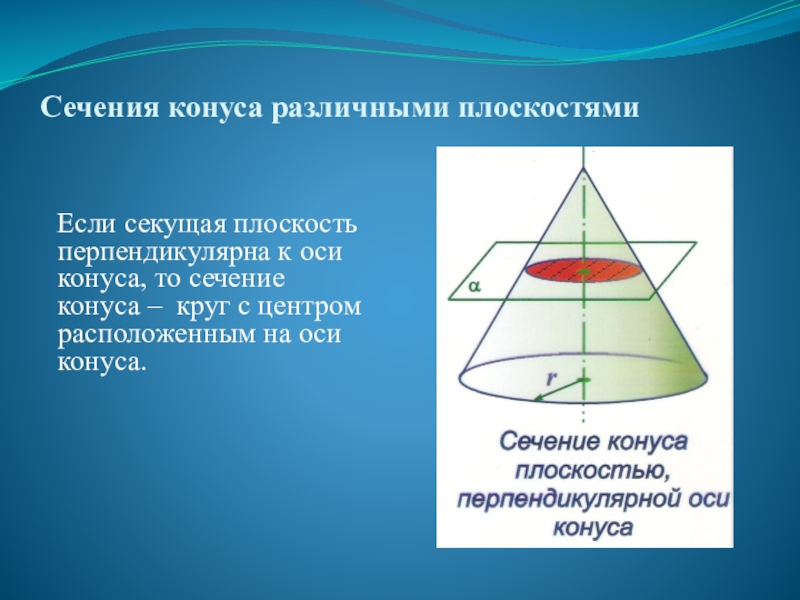
- 22. Сечения конуса различными плоскостямиЕсли секущая плоскость перпендикулярна
- 23. Конические сечения конуса – линии пересечения секущих
- 24. КОНУСКасательная плоскость – плоскость, проходящая через образующую и перпендикулярная плоскости осевого сечения
- 25. Усечённый конусУсеченным конусом называется часть конуса, ограниченная его основанием и сечением, перпендикулярным к его оси.
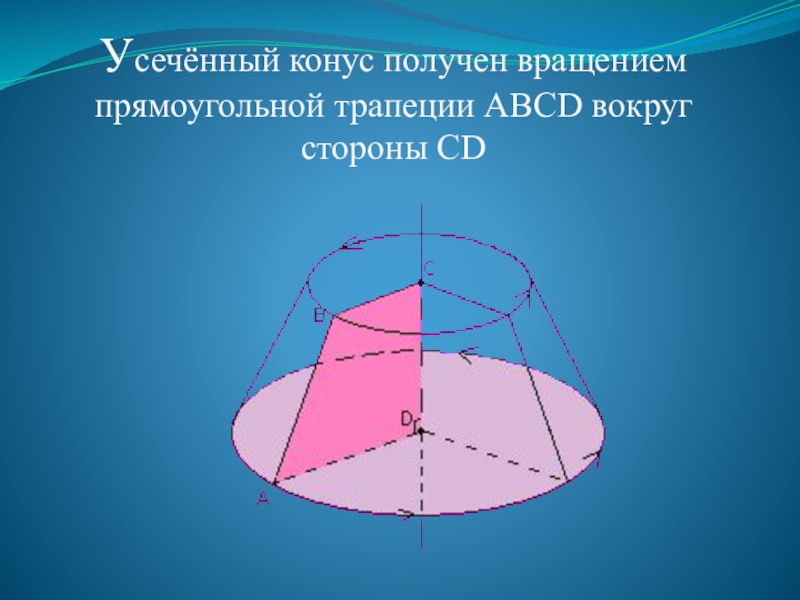
- 26. Усечённый конус получен вращением прямоугольной трапеции АВСD вокруг стороны CD
- 27. Площадь боковой поверхности усечённого конуса.Площадь боковой поверхности
- 28. Площадь полной поверхности усечённого конусаПлощадь полной поверхности усечённого конуса : Sпол= πl (R+r)+πR2+ πr2
- 29. Найдите площадь полной поверхности тела, полученного
- 30. Вписанная пирамидаПирамида называется вписанной в конус, если
- 31. Описанная пирамидаПирамида называется описанной около конуса, если
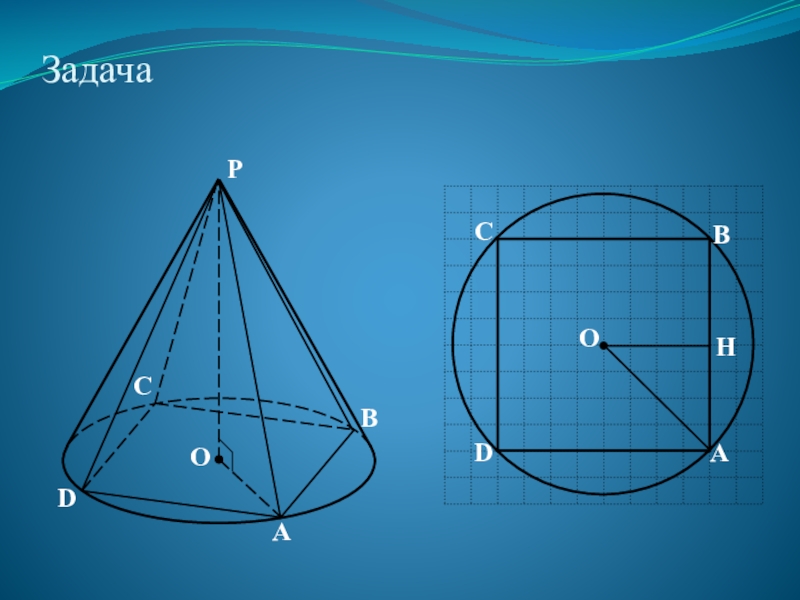
- 32. Задача Вокруг конуса описана правильная четырехугольная пирамида.
- 33. Слайд 33
- 34. Слайд 34
- 35. Задача В конус вписана правильная четырехугольная пирамида.
- 36. Задача
- 37. Слайд 37
- 38. Объём конусаОбъём конуса равен одной трети произведения площади основания на высоту:
- 39. Объём усечённого конусаОбъём усечённого конуса, высота которого
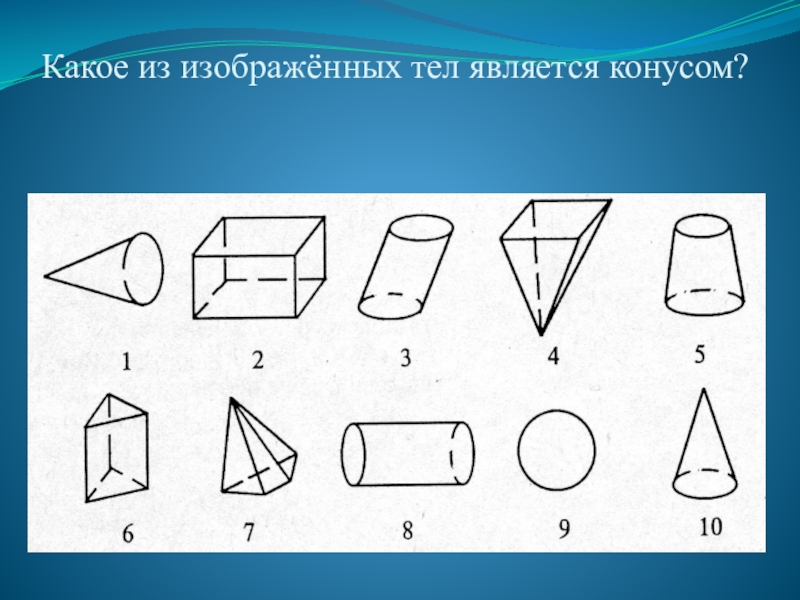
- 40. Какое из изображённых тел является конусом?
- 41. Ответьте на вопрос и запишите ответы в
- 42. Проверь себяЗадание 1: 1; 5; 10.Задание 2:1. Круг.2. Образующая.3. Нет.4. Усечённый конус.5. Сектор.
Нас окружает множество предметов
Слайд 1Департамент образования города Москвы
Северо-Западное окружное управление образования
Презентация по геометрии на тему
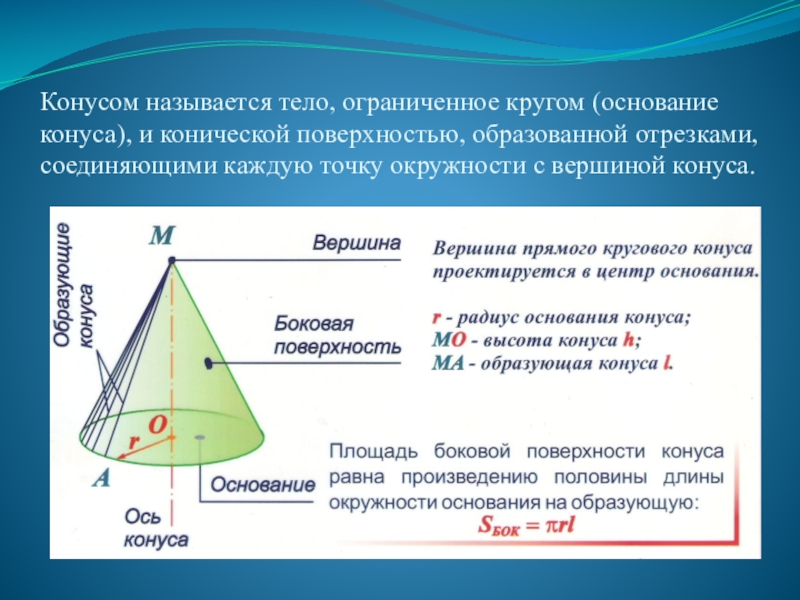
Слайд 4Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью, образованной
отрезками, соединяющими каждую точку окружности с вершиной конуса.
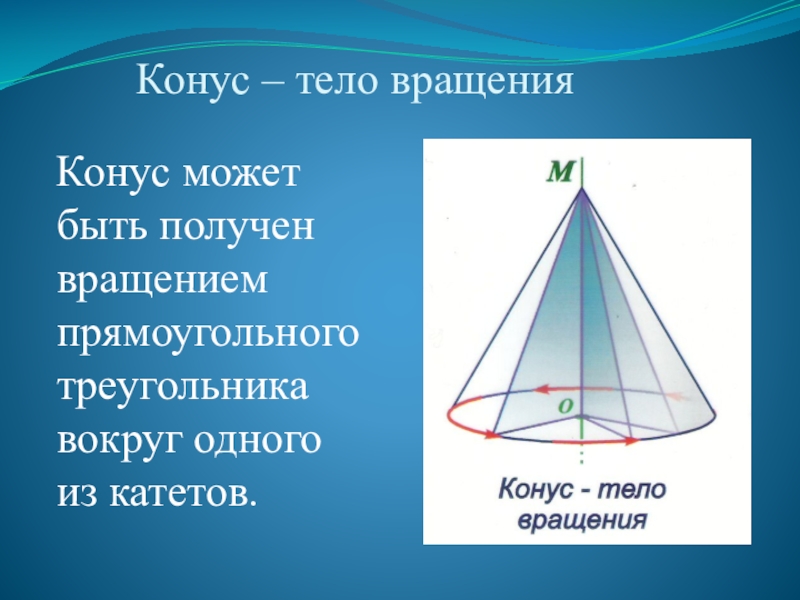
Слайд 5Конус – тело вращения
Конус может быть получен вращением прямоугольного треугольника вокруг
одного из катетов.
Слайд 6Так выглядит развертка конуса
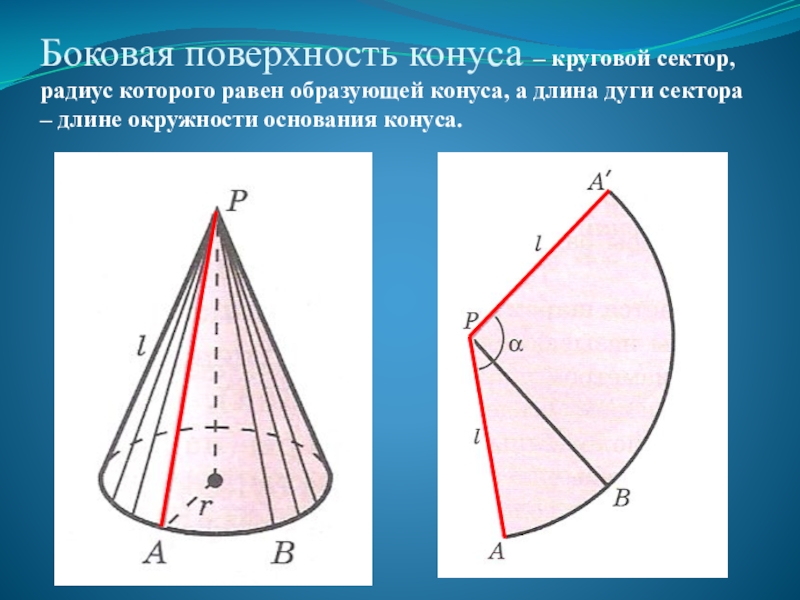
Развёрткой конуса является круговой сектор, у
которого радиус равен образующей конуса R=ℓ,
а длина дуги равна длине окружности основания конуса L=C=2πR
а длина дуги равна длине окружности основания конуса L=C=2πR
ℓ
α
С = 2πR
Формулы
для вычисления боковой поверхности
и полной поверхности конуса:
Sбок.= πRℓ
Sосн.= πR²
Sп.п.к. =Sбок.+Sосн.= πR(R+ℓ)
Слайд 7Боковая поверхность конуса – круговой сектор, радиус которого равен образующей конуса,
а длина дуги сектора – длине окружности основания конуса.
Слайд 8Площадь боковой поверхности конуса равна произведению половины длины окружности основания на
образующую:
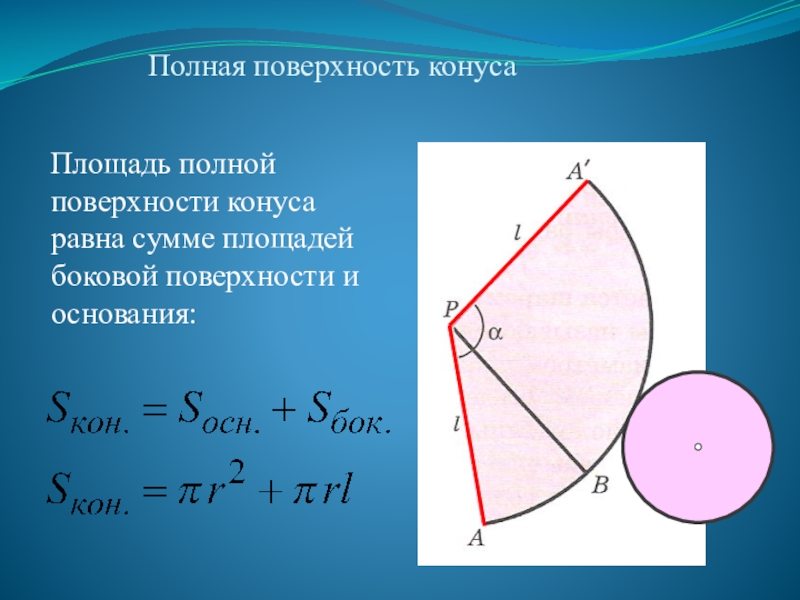
Слайд 9Полная поверхность конуса
Площадь полной поверхности конуса равна сумме площадей боковой поверхности
и основания:
Слайд 11Для решения задачи надо измерить:
Длину окружности основания воронки:
С= 12м
и глубину по склону: ℓ=1,5 м
Найти: Sбок.=?
Решение: Sбок.= πRℓ
С= 2πR
R=С:2π
Sбок.= πRℓ= πСℓ:2π=Сℓ:2
Sбок.=12·1,5:2= 9м²
Ответ: 9 м²
и глубину по склону: ℓ=1,5 м
Найти: Sбок.=?
Решение: Sбок.= πRℓ
С= 2πR
R=С:2π
Sбок.= πRℓ= πСℓ:2π=Сℓ:2
Sбок.=12·1,5:2= 9м²
Ответ: 9 м²
ℓ
С
Слайд 12Задача
Сколько квадратных метров брезента потребуется для сооружения
палатки конической формы высотой 4 метра и диаметром основания 6 метров ?
4
6
Слайд 13
Решение:
Sбок.= πRℓ
R=D:2 = 6:2 = 3(м)
ℓ= √
Н² +R² = √4² + 3² = 5
Sбок.≈ 3,14· 3·5 ≈ 45,7(м²)
Ответ: ≈ 46 м²
Sбок.≈ 3,14· 3·5 ≈ 45,7(м²)
Ответ: ≈ 46 м²
4
3
3
Дано: Н=4 м
D=6 м
Найти: Sбок.=?
6
Слайд 14Задача
F
О
Фонарь установлен на высоте 8 м.
Угол рассеивания фонаря 120°.
Определите, какую поверхность освещает фонарь.
120°
8м
Слайд 16Решение:
FАО= (180°-120°)/2=30°
FA=8•2=16 (катет, лежащий против угла в 30°)
АО= √ FA²-FO² = √16²-8² = 8√3 (по теореме Пифагора)
S = π (8√3)² =132π ≈ 414,5 м²
Ответ: 414,5 м²
S = π (8√3)² =132π ≈ 414,5 м²
Ответ: 414,5 м²
Слайд 17Задача
Образующая конуса, равная 12 см, наклонена к плоскости основания под углом
45°. Найдите площадь основания конуса.
12 см
А
О
В
45°
Слайд 19Задача 5. Высота конуса равна 12, а радиус основания равен 5.
Найдите площадь полной поверхности конуса. В ответе запишите S/π.
Слайд 20СЕЧЕНИЯ КОНУСА
Сечения, проходящее
через ось(осевые)
Сечения, перпендикулярные оси (поперечные)
Сечение, проходящее через вершину,
не содержащее ось конуса
Равнобедренный треугольник: боковые стороны – образующие, основание – диаметр конуса
Если равносторонний треугольник – конус называется равносторонним
Круг радиуса меньшего, радиуса основания
Равнобедренный треугольник: боковые стороны – образующие, основание – хорда окружности основания
Слайд 21Сечения конуса различными плоскостями
Секущая плоскость проходит через ось конуса.
Осевое сечение
– равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса.
Слайд 22Сечения конуса различными плоскостями
Если секущая плоскость перпендикулярна к оси конуса, то
сечение конуса – круг с центром расположенным на оси конуса.
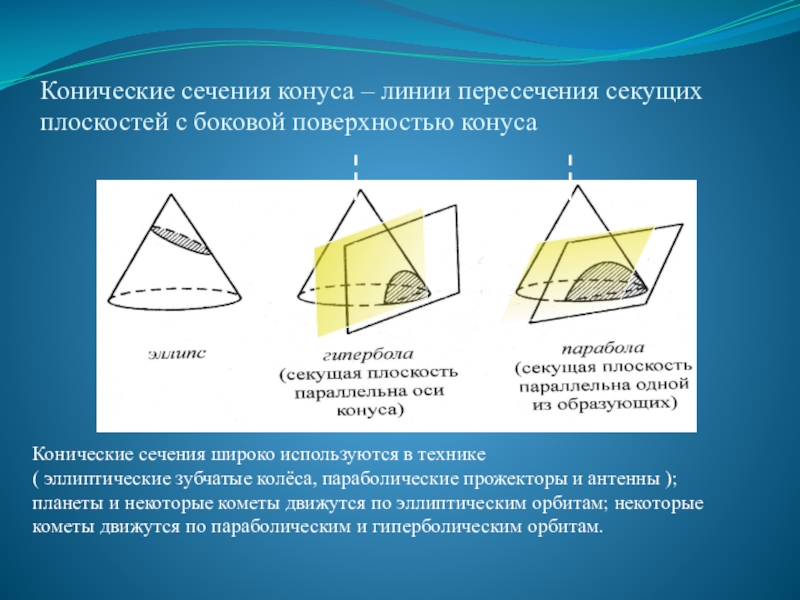
Слайд 23Конические сечения конуса – линии пересечения секущих плоскостей с боковой поверхностью
конуса
Конические сечения широко используются в технике
( эллиптические зубчатые колёса, параболические прожекторы и антенны ); планеты и некоторые кометы движутся по эллиптическим орбитам; некоторые кометы движутся по параболическим и гиперболическим орбитам.
Слайд 24КОНУС
Касательная плоскость –
плоскость, проходящая
через образующую
и перпендикулярная
плоскости осевого
сечения
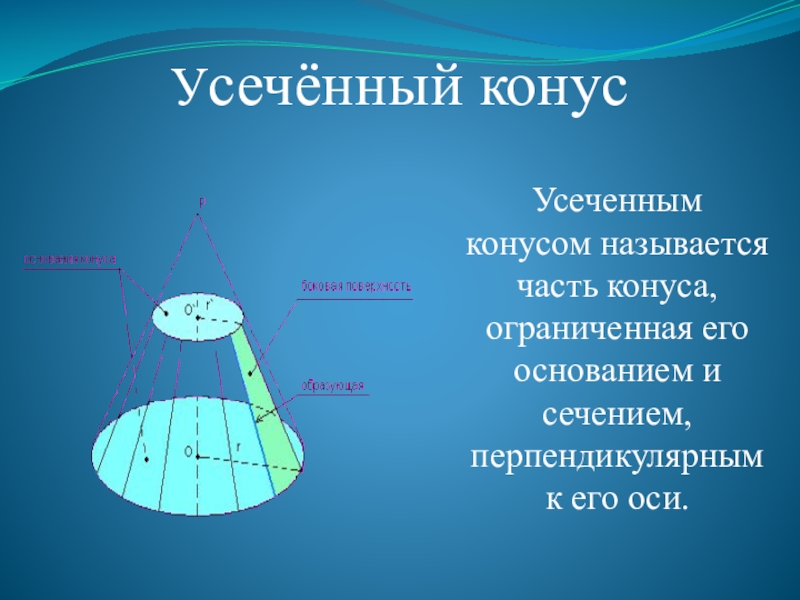
Слайд 25Усечённый конус
Усеченным конусом называется часть конуса, ограниченная его основанием и сечением,
перпендикулярным к его оси.
Слайд 27Площадь боковой поверхности усечённого конуса.
Площадь боковой поверхности усечённого конуса равна произведению
полусуммы длин окружностей оснований на образующую:
Sбок= π (r + R) l
Sбок= π (r + R) l
Слайд 28Площадь полной поверхности усечённого конуса
Площадь полной поверхности усечённого конуса :
Sпол=
πl (R+r)+πR2+ πr2
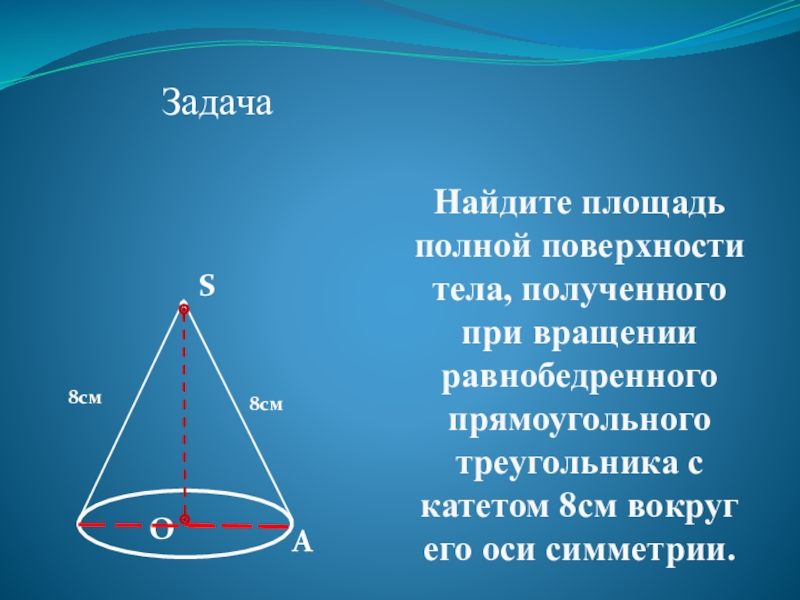
Слайд 29 Найдите площадь полной поверхности тела, полученного при вращении равнобедренного прямоугольного треугольника
с катетом 8см вокруг его оси симметрии.
Задача
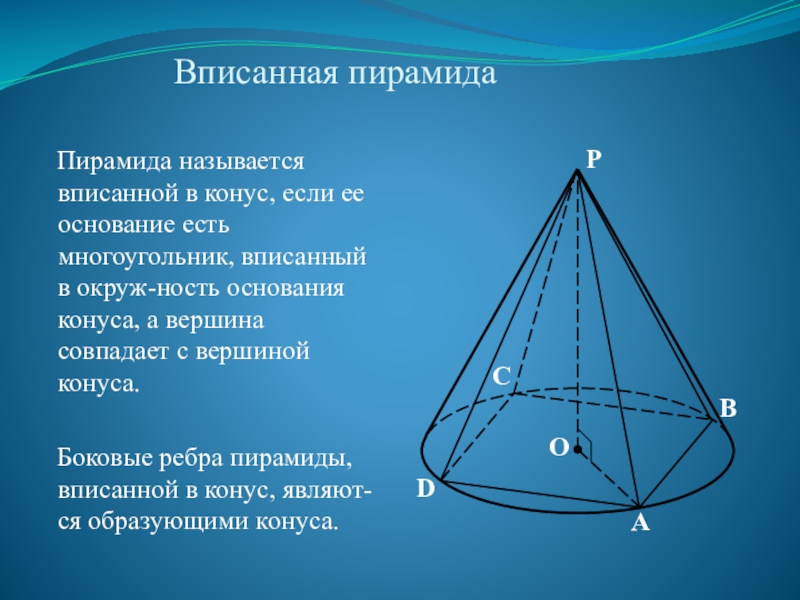
Слайд 30Вписанная пирамида
Пирамида называется вписанной в конус, если ее основание есть многоугольник,
вписанный в окруж-ность основания конуса, а вершина совпадает с вершиной конуса.
Боковые ребра пирамиды, вписанной в конус, являют-ся образующими конуса.
Боковые ребра пирамиды, вписанной в конус, являют-ся образующими конуса.
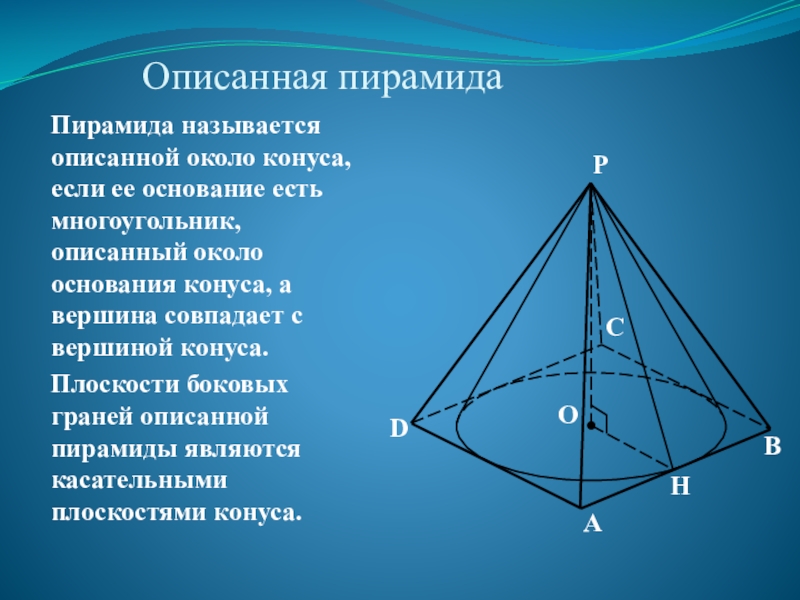
Слайд 31Описанная пирамида
Пирамида называется описанной около конуса, если ее основание есть многоугольник,
описанный около основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
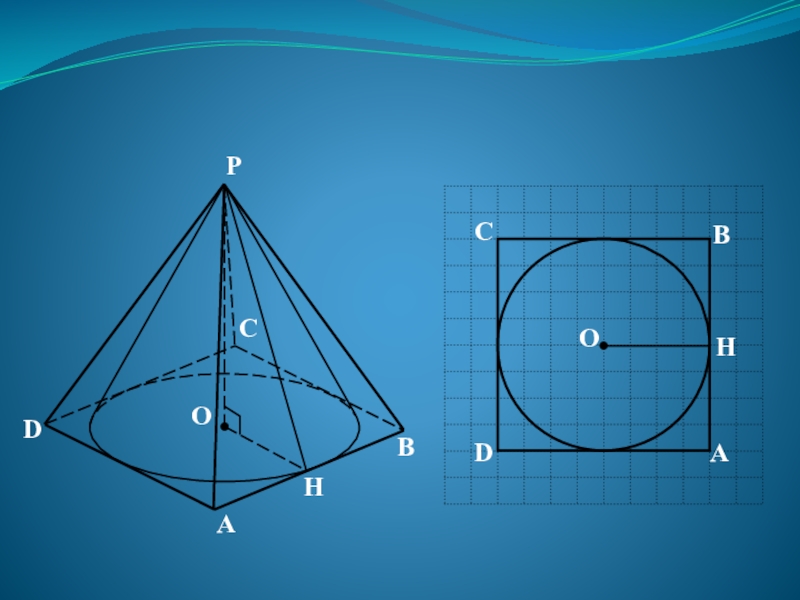
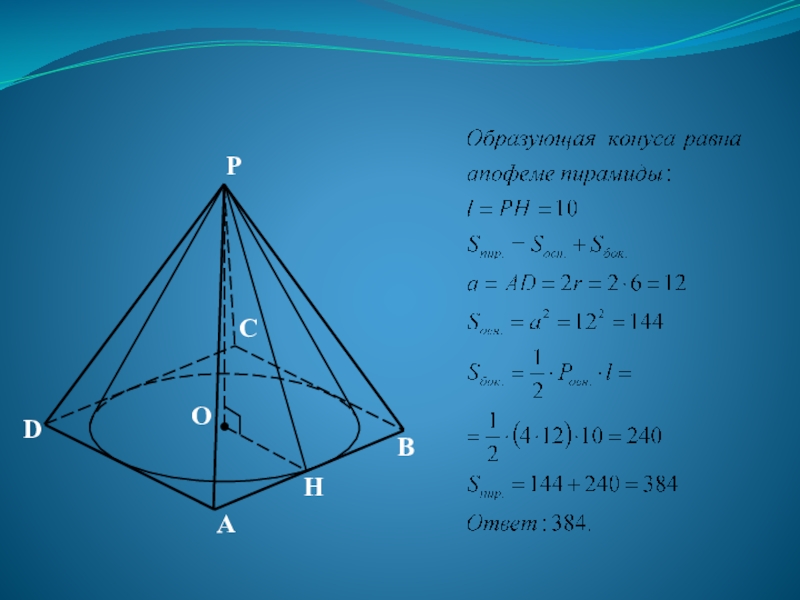
Слайд 32Задача
Вокруг конуса описана правильная четырехугольная пирамида. Найдите полную поверхность пирамиды,
если радиус основания конуса равен 6, а образующая конуса равна 10.
Слайд 35Задача
В конус вписана правильная четырехугольная пирамида. Найдите полную поверхность конуса,
если боковое ребро пирамиды равно 15, а ее высота равна 9. В ответе запишите S/π.
Слайд 39Объём усечённого конуса
Объём усечённого конуса, высота которого равна h,а площади оснований
равны S и S1:
Слайд 41Ответьте на вопрос и запишите ответы в столбик. Из первых букв
составьте слово.
Как называется:
1. Фигура, полученная при поперечном сечении конуса?
2. Отрезок, соединяющий вершину с окружностью основания?
3. Имеет ли конус центр симметрии?
4. Тело, полученное при пересечении конуса плоскостью, параллельной основанию?
5. Фигура, являющаяся боковой поверхностью конуса?
Слайд 42Проверь себя
Задание 1: 1; 5; 10.
Задание 2:
1. Круг.
2. Образующая.
3. Нет.
4.
Усечённый конус.
5. Сектор.
5. Сектор.
