- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку на тему Сумма углов треугольника
Содержание
- 1. Презентация к уроку на тему Сумма углов треугольника
- 2. Цели:Образовательные: Актуализировать знания о треугольнике;Изучить теорему о
- 3. Развивающие: Развивать геометрическое мышление и интерес к
- 4. Задачи урока:Ввести понятие «сумма углов треугольника», «внешний
- 5. Тип урока: урок усвоения новых знаний.Методы обучения:
- 6. Литература:Геометрия 7-9 классы: учеб. Для общеобразовательных учреждений
- 7. План урока:Организационный момент (2 минуты).Актуализация знаний (6
- 8. Ход урокаОрганизационный момент.Включает в себя приветствие учеников,
- 9. II. Актуализация знаний.С геометрической фигурой «треугольник» мы
- 10. Сформулируйте определение треугольника?Треугольником называется фигура, которая состоит
- 11. Из каких элементов состоит треугольник?Треугольник состоит из трех точек и трех отрезков
- 12. Итак, о треугольнике мы знаем уже достаточно
- 13. Практическая работа (способствует актуализации знаний и навыков
- 14. Ребята, обратите внимание, у меня в руках
- 15. Возьмем треугольник красного цвета, а два других
- 16. Посмотрите внимательно, что у нас получилось? Какой угол составляют вместе эти три угла? Развернутый
- 17. Какова градусная мера этого угла? 180 градусовЗначит,
- 18. К какому выводу мы пришли?Сумма углов треугольника
- 19. III. Объяснение нового материалаВ математике практическая работа
- 20. Какую теорему нам нужно доказать?Сумма углов треугольника равна 180 градусов
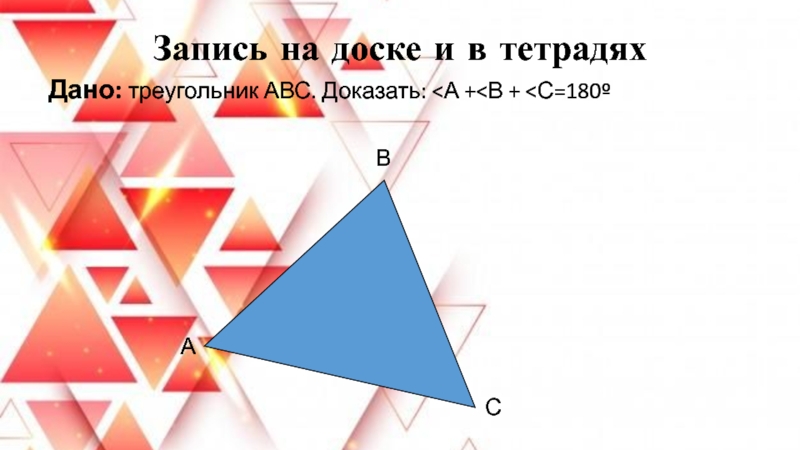
- 21. Запись на доске и в тетрадяхДано: треугольник АВС. Доказать:
- 22. ДоказательствоЧто нам дано? Дан треугольникПостройте у себя
- 23. Через вершину С проведем прямую а параллельную
- 24. Правильно, теперь посмотрите какой у нас ∠ С?Развернутый
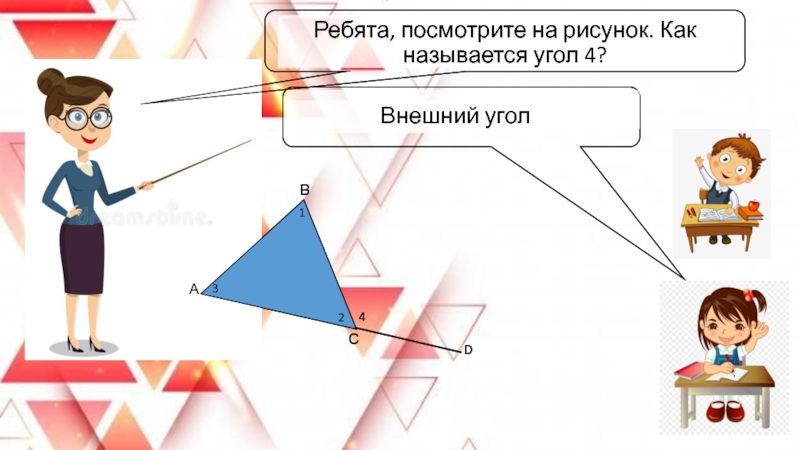
- 25. Ребята, посмотрите на рисунок. Как называется угол 4?Внешний уголАСВ2134D
- 26. Верно. Давайте вместе сформулируем определение внешнего угла.Внешним
- 27. Давайте докажем, что внешний угол треугольника равен
- 28. IV. Закрепление изученного материалаИтак, теорема о сумме
- 29. Модели треугольниковЗадание выполняется самостоятельно каждым учеником. Решения и ответы обсуждаются.
- 30. Спасибо за просмотр
Цели:Образовательные: Актуализировать знания о треугольнике;Изучить теорему о сумме углов треугольника и классифицировать треугольники по углам и сторонам;Сформировать умение применять теорему о сумме углов треугольника при решении задач.
Слайд 2Цели:
Образовательные:
Актуализировать знания о треугольнике;
Изучить теорему о сумме углов треугольника и
классифицировать треугольники по углам и сторонам;
Сформировать умение применять теорему о сумме углов треугольника при решении задач.
Сформировать умение применять теорему о сумме углов треугольника при решении задач.
Слайд 3Развивающие:
Развивать геометрическое мышление и интерес к предмету;
Развивать познавательную и творческую
деятельность учащихся;
Развивать математическую речь и умение самостоятельно добывать знания.
Воспитательные:
Развивать личностные качества учащихся, такие как целеустремленность, настойчивость, аккуратность, умение работать в коллективе.
Развивать математическую речь и умение самостоятельно добывать знания.
Воспитательные:
Развивать личностные качества учащихся, такие как целеустремленность, настойчивость, аккуратность, умение работать в коллективе.
Слайд 4Задачи урока:
Ввести понятие «сумма углов треугольника», «внешний угол треугольника», «прямоугольный треугольник»,
«остроугольный треугольник», «тупоугольный треугольник»;
Сформулировать теорему о сумме углов треугольника, следствие из теоремы о сумме углов треугольника;
Доказать сформулированную теорему;
Закрепить полученную теорему и следствие из теоремы при решении задач.
Сформулировать теорему о сумме углов треугольника, следствие из теоремы о сумме углов треугольника;
Доказать сформулированную теорему;
Закрепить полученную теорему и следствие из теоремы при решении задач.
Слайд 5
Тип урока: урок усвоения новых знаний.
Методы обучения: репродуктивный, объяснительно-иллюстративный, эвристический.
Оборудование: презентация,
мультимедийная установка, учебник, чертежные инструменты, треугольники из разноцветного картона.
Слайд 6Литература:
Геометрия 7-9 классы: учеб. Для общеобразовательных учреждений / Л.С. Атанасян, В.Ф.
Бутузов, С.Б. Кадомцев и др. –
М.: Просвещение, 2014.
Поурочные разработки по геометрии 7 класс по учебнику Л.С. Атанасяна и др. Геометрия 7-9 кл. / Гаврилова Н.Ф. – М.: Просвещение, 2010.
Упражнения в обучении математике / Г.И. Саранцев. – 2-е изд., дораб. – М.: Просвещение, 2005.
Поурочные разработки по геометрии 7 класс по учебнику Л.С. Атанасяна и др. Геометрия 7-9 кл. / Гаврилова Н.Ф. – М.: Просвещение, 2010.
Упражнения в обучении математике / Г.И. Саранцев. – 2-е изд., дораб. – М.: Просвещение, 2005.
Слайд 7План урока:
Организационный момент (2 минуты).
Актуализация знаний (6 минут).
Объяснение нового материала (12
минут).
Закрепление нового материала (20 минут).
Подведение итогов урока (3 минуты).
Постановка домашнего задания (2 минуты).
Закрепление нового материала (20 минут).
Подведение итогов урока (3 минуты).
Постановка домашнего задания (2 минуты).
Слайд 8Ход урока
Организационный момент.
Включает в себя приветствие учеников, проверку отсутствующих, запись учениками
числа, классной работы и темы урока.
Запись на доске и в тетрадях.
Дата. Классная работа. «Сумма углов треугольника».
Запись на доске и в тетрадях.
Дата. Классная работа. «Сумма углов треугольника».
Слайд 9II. Актуализация знаний.
С геометрической фигурой «треугольник» мы познакомились на предыдущих уроках.
Давайте повторим то, что нам известно о треугольнике.
Слайд 10Сформулируйте определение треугольника?
Треугольником называется фигура, которая состоит из трех точек, не
лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки
Слайд 12Итак, о треугольнике мы знаем уже достаточно много.
А как вы
думаете, чему равна сумма углов любого треугольника?
(Заслушать ответы)
Давайте проверим, верны ли ваши ответы с помощью практической работы.
(Заслушать ответы)
Давайте проверим, верны ли ваши ответы с помощью практической работы.
Слайд 13Практическая работа
(способствует актуализации знаний и навыков самопознания)
Нарисуйте произвольный треугольник,
измерьте углы треугольника с помощью транспортира и найдите их сумму. Результаты запишите в тетрадь (заслушать полученные ответы).
Выясняем, что сумма углов у всех получилась разная. У кого-то получилось 180º, у кого-то чуть больше или чуть меньше (так может получиться, потому что неточно приложили транспортир, небрежно выполнили подсчет и т.д.). но тем не менее ваши результаты близки к 180º.
Выясняем, что сумма углов у всех получилась разная. У кого-то получилось 180º, у кого-то чуть больше или чуть меньше (так может получиться, потому что неточно приложили транспортир, небрежно выполнили подсчет и т.д.). но тем не менее ваши результаты близки к 180º.
Слайд 14Ребята, обратите внимание, у меня в руках три равных треугольника. Как
можно в этом убедиться? Наложите один треугольник на другой, и вы проверите это.
Слайд 15Возьмем треугольник красного цвета, а два других треугольника приложим рядом с
первым таким образом, чтобы у одной вершины оказалось три разных угла, а стороны их совпадали.
Слайд 16Посмотрите внимательно, что у нас получилось?
Какой угол составляют вместе эти
три угла?
Развернутый
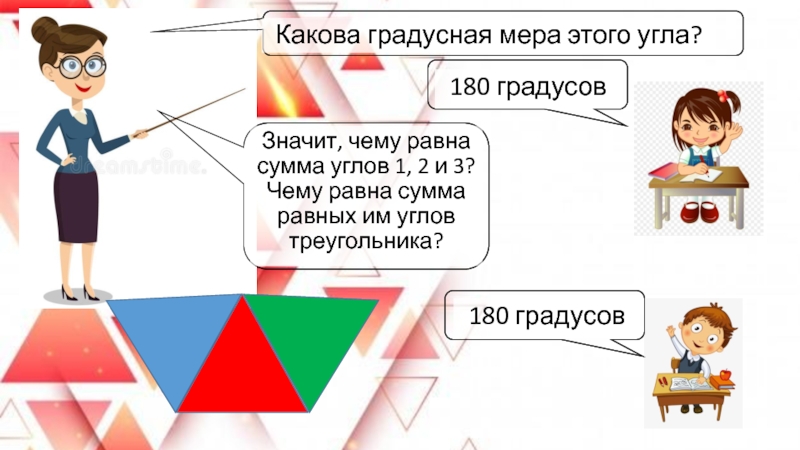
Слайд 17Какова градусная мера этого угла?
180 градусов
Значит, чему равна сумма углов
1, 2 и 3? Чему равна сумма равных им углов треугольника?
180 градусов
Слайд 18К какому выводу мы пришли?
Сумма углов треугольника равна 180 градусов
Выполнив практическую
работу, мы установили, что сумма углов треугольника равна 180 градусов
Слайд 19III. Объяснение нового материала
В математике практическая работа дает возможность лишь сделать
какое-то утверждение, но его нужно доказать. Как называется утверждение, справедливость которого устанавливается путем доказательства?
Теорема
Слайд 22Доказательство
Что нам дано?
Дан треугольник
Постройте у себя в тетрадях произвольный треугольник
и обозначьте его вершины А, В и С. Что требуется доказать?
Что сумма углов треугольника равна 180.
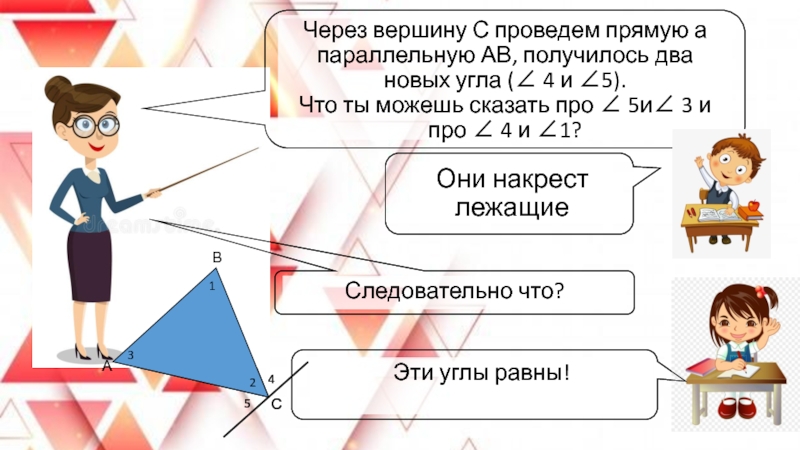
Слайд 23Через вершину С проведем прямую а параллельную АВ, получилось два новых
угла (∠ 4 и ∠5).
Что ты можешь сказать про ∠ 5и∠ 3 и про ∠ 4 и ∠1?
Они накрест лежащие
Следовательно что?
Эти углы равны!
А
С
В
2
1
3
4
5
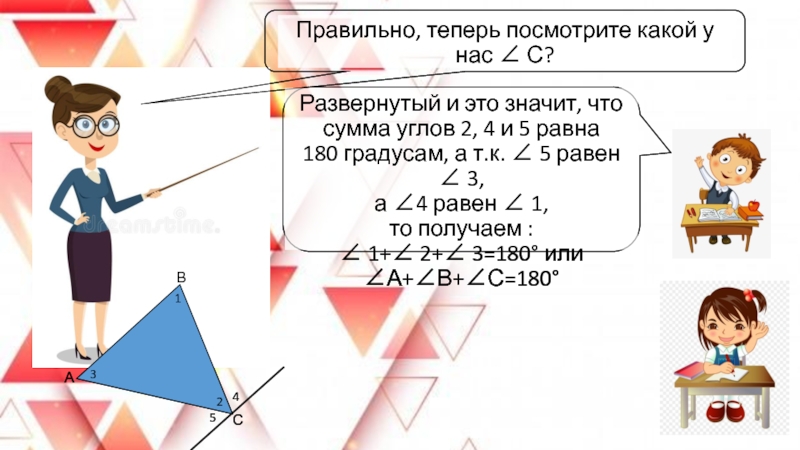
Слайд 24Правильно, теперь посмотрите какой у нас ∠ С?
Развернутый и это значит, что
сумма углов 2, 4 и 5 равна
180 градусам, а т.к. ∠ 5 равен ∠ 3,
а ∠4 равен ∠ 1,
то получаем : ∠ 1+∠ 2+∠ 3=180° или ∠А+∠В+∠С=180°
А
С
В
2
1
3
4
5
Слайд 26Верно. Давайте вместе сформулируем определение внешнего угла.
Внешним углом треугольника называется угол, смежный
с каким-нибудь углом этого треугольника.
(Запись на доске и в тетрадях)
(Запись на доске и в тетрадях)
Слайд 27Давайте докажем, что внешний угол треугольника равен сумме двух углов треугольника,
не смежных с ним. Обратимся к рисунку, на котором ∠DCB – внешний угол, смежный с ∠ACB данного треугольника.
Так как ∠DCB + ∠ACB =180° градусов, а по теореме о сумме углов треугольника (∠CAB + ∠ABC) + ∠ACB = 180° градусов, то ∠DCB = ∠CAB + ∠ABC, что и требовалось доказать.
Так как ∠DCB + ∠ACB =180° градусов, а по теореме о сумме углов треугольника (∠CAB + ∠ABC) + ∠ACB = 180° градусов, то ∠DCB = ∠CAB + ∠ABC, что и требовалось доказать.
Слайд 28IV. Закрепление изученного материала
Итак, теорема о сумме углов треугольника доказана. Давайте
приступим к решению задач.
Вычислите все неизвестные углы треугольника
Вычислите все неизвестные углы треугольника