- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Четыре замечательные точки треугольника
Содержание
- 1. Презентация по геометрии Четыре замечательные точки треугольника
- 2. Домашнее задание
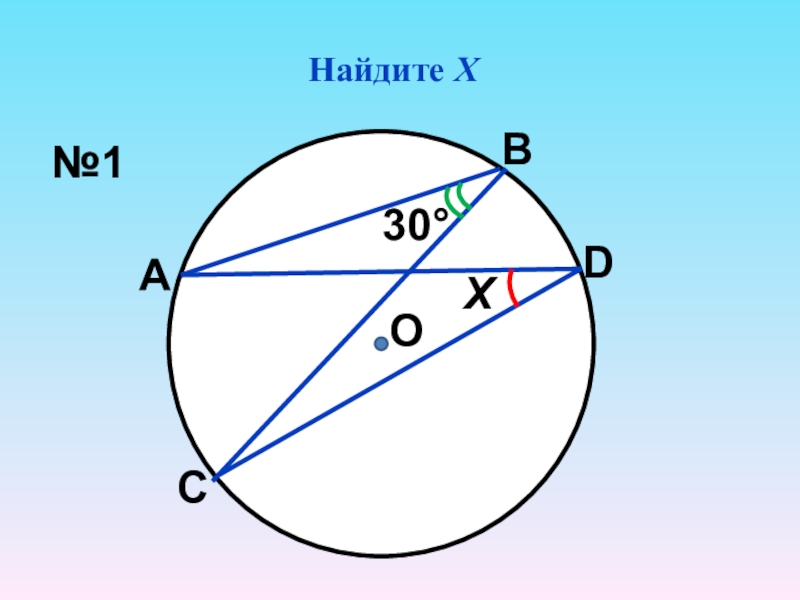
- 3. Найдите ХО30°Х№1АВСD
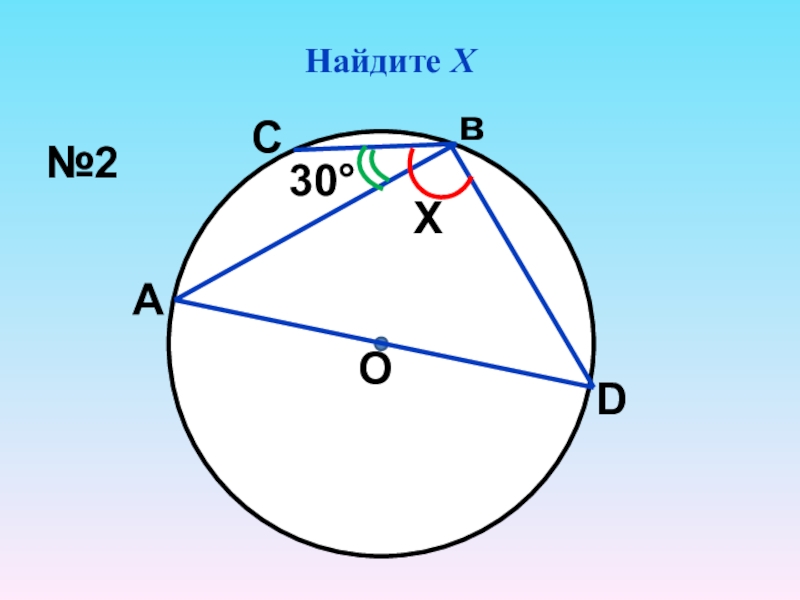
- 4. Найдите ХО30°ХАСвD№2
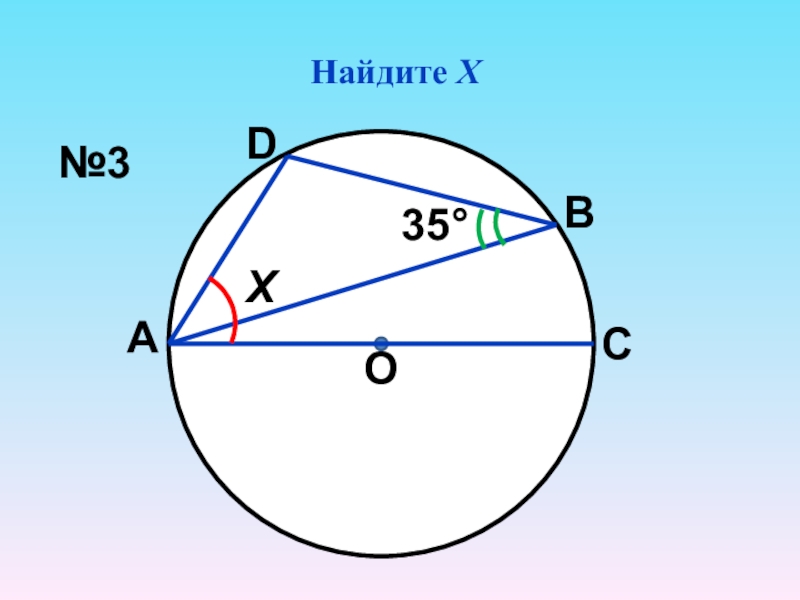
- 5. Найдите ХО35°ХАСВD№3
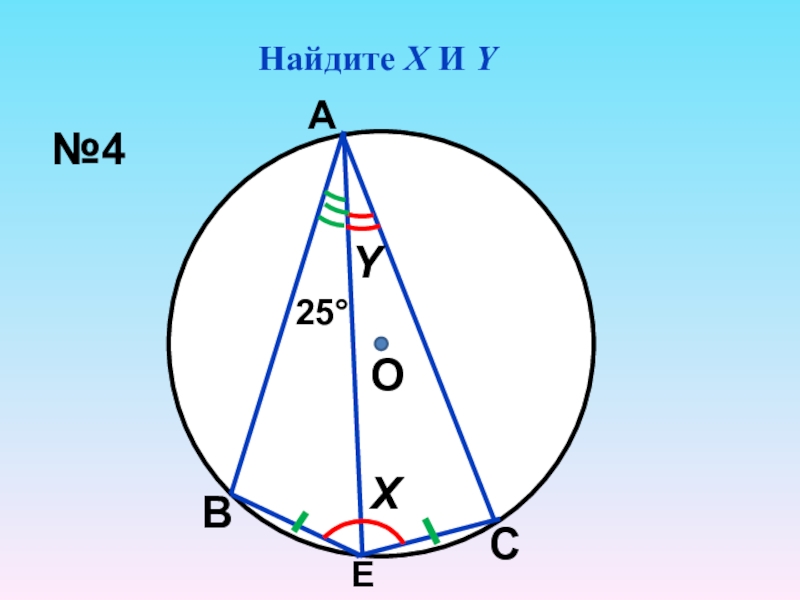
- 6. Найдите Х И YОХY25°АВСЕ№4
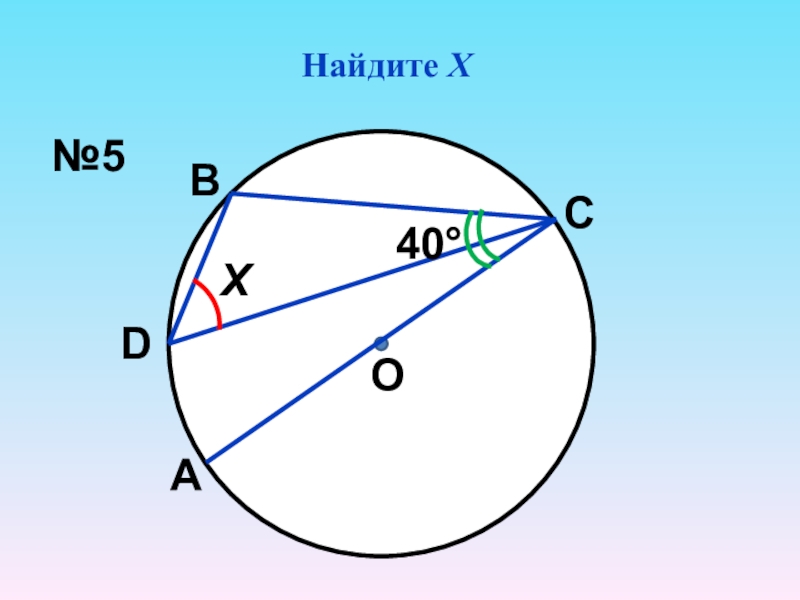
- 7. Найдите ХХО40°АDВС№5
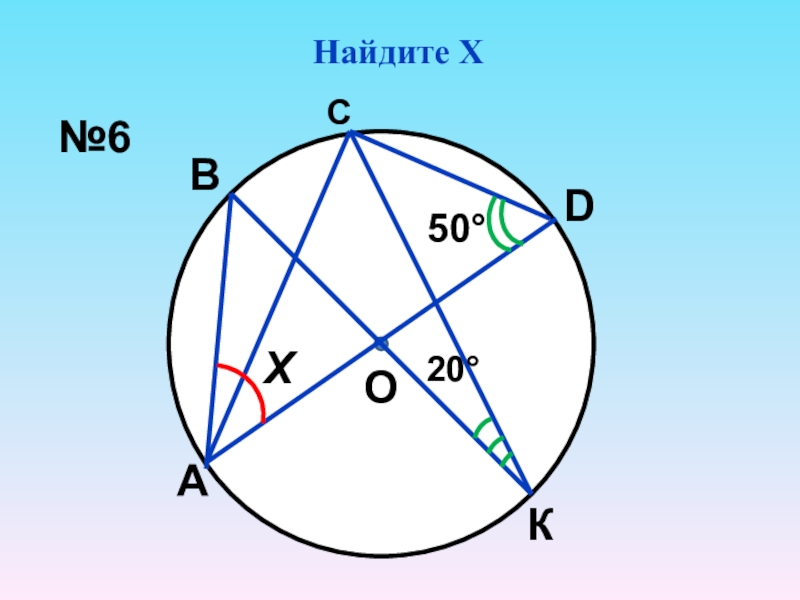
- 8. Найдите ХВКАDОСХ50°20°№6
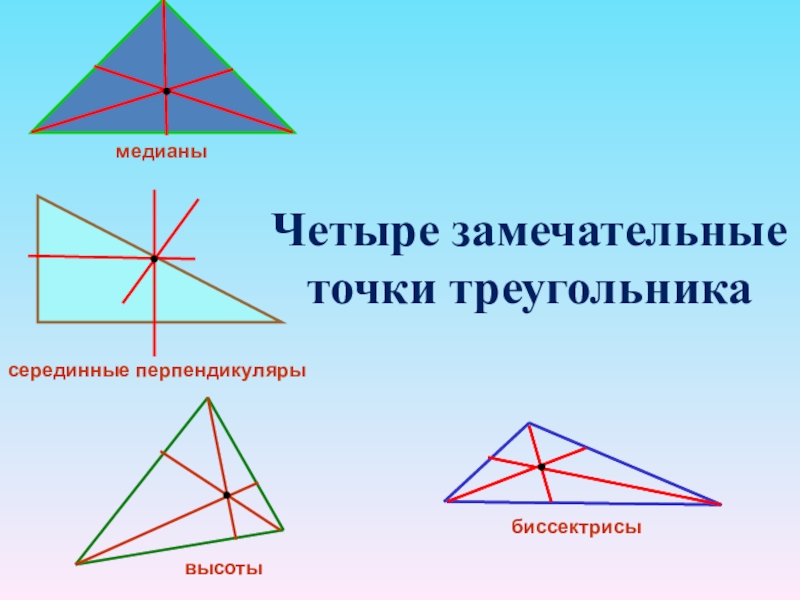
- 9. Четыре замечательные точки треугольникавысотыбиссектрисысерединные перпендикулярымедианы
- 10. Свойство биссектрисы неразвёрнутого углаТеорема1. Каждая точка биссектрисы
- 11. Серединный перпендикуляр к отрезкуТеорема 1. Каждая точка
- 12. Первая замечательная точка треугольникаТеорема. Биссектрисы треугольника пересекаются в одной точке.
- 13. Вторая замечательная точка треугольникаТеорема. Серединные перпендикуляры
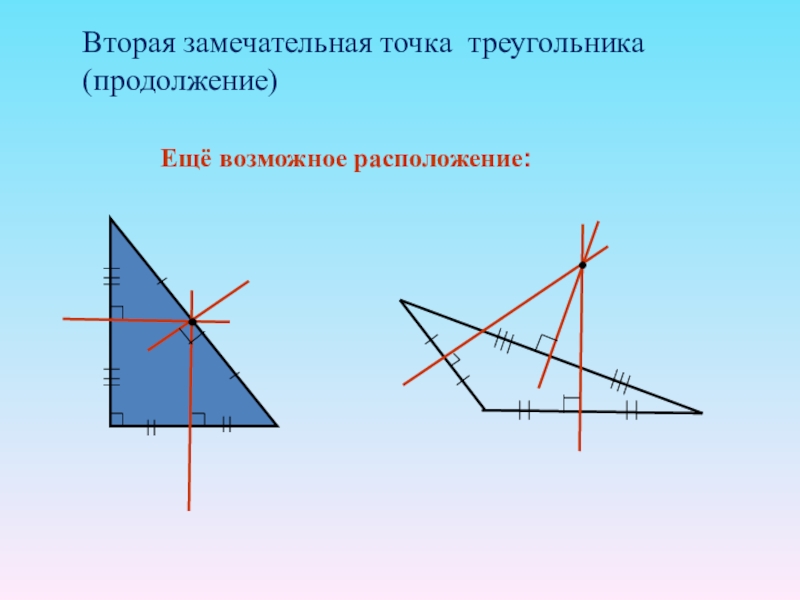
- 14. Вторая замечательная точка треугольника (продолжение)Ещё возможное расположение:
- 15. Третья замечательная точка треугольникаТеорема. Медианы треугольника
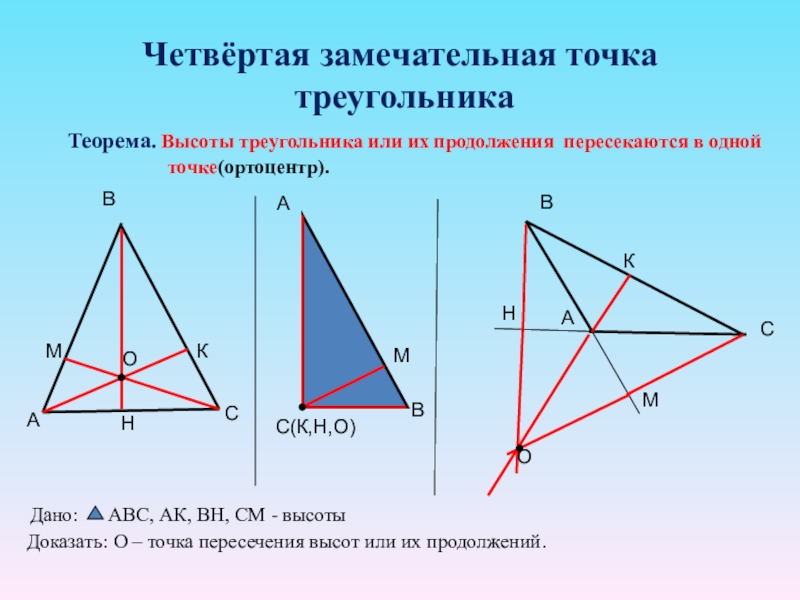
- 16. Четвёртая замечательная точка треугольникаТеорема. Высоты треугольника
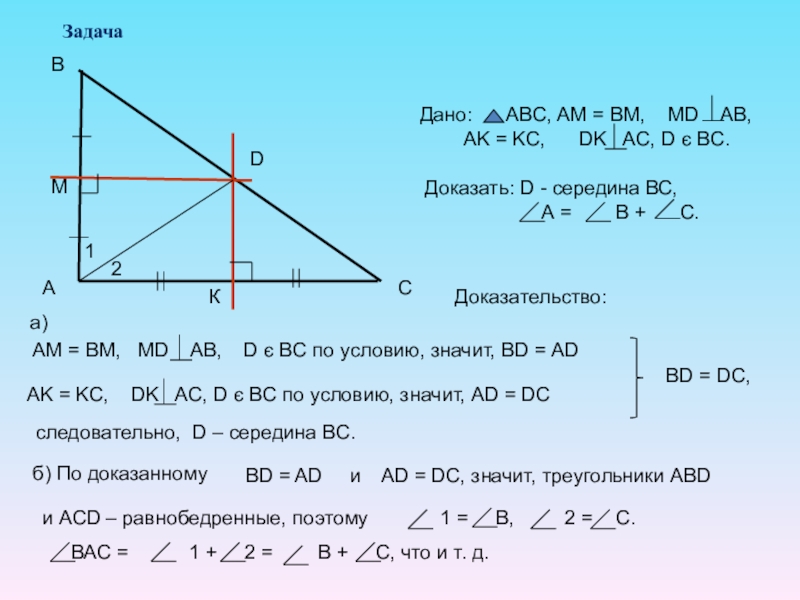
- 17. Доказательство:следовательно, D – середина ВС.
Слайд 10Свойство биссектрисы неразвёрнутого угла
Теорема1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от
его сторон.
Доказать: МЕ = МК
Теорема 2 ( обратная).Точка, лежащая внутри неразвёрнутого угла и
равноудалённая от его сторон, лежит на биссектрисе
этого угла.
Обобщённая теорема: биссектриса неразвёрнутого угла – множество точек плоскости,
равноудалённых от сторон этого угла.
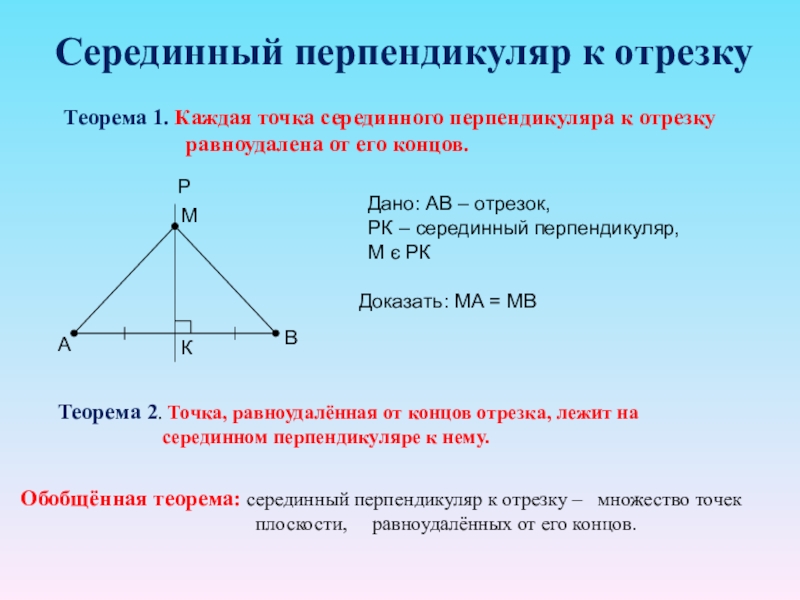
Слайд 11Серединный перпендикуляр к отрезку
Теорема 1. Каждая точка серединного перпендикуляра к отрезку
Дано: АВ – отрезок,
РК – серединный перпендикуляр,
М є РК
Доказать: МА = МВ
Теорема 2. Точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к нему.
Обобщённая теорема: серединный перпендикуляр к отрезку – множество точек
плоскости, равноудалённых от его концов.
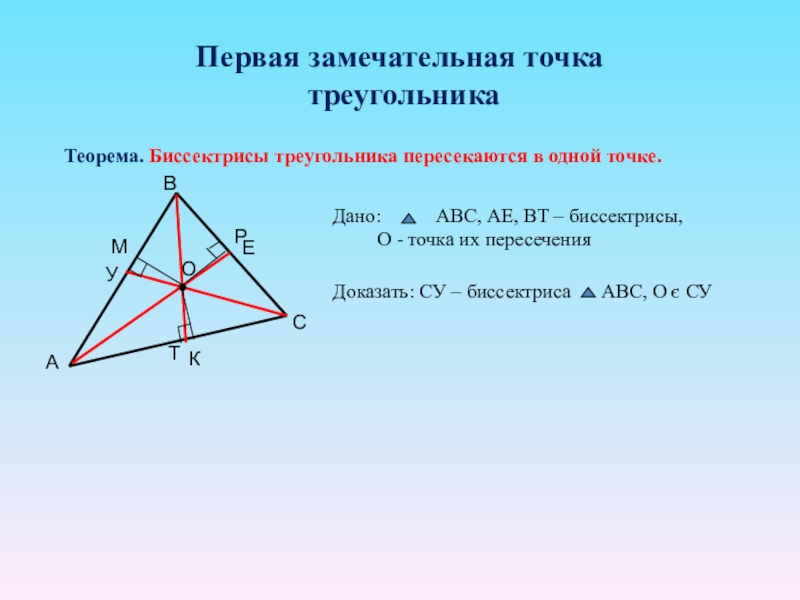
Слайд 12Первая замечательная точка
треугольника
Теорема. Биссектрисы треугольника пересекаются в одной точке.
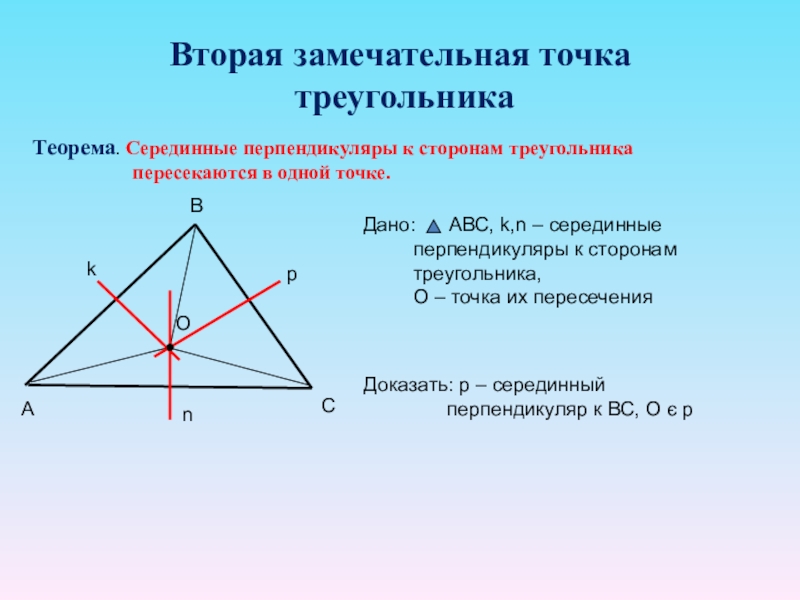
Слайд 13Вторая замечательная точка
треугольника
Теорема. Серединные перпендикуляры к сторонам треугольника
Доказать: р – серединный
перпендикуляр к ВС, О є р
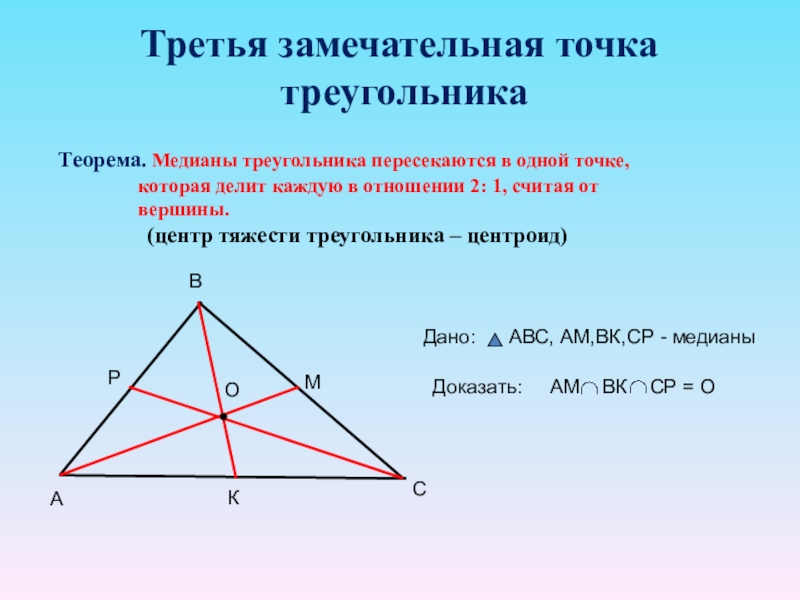
Слайд 15Третья замечательная точка
треугольника
Теорема. Медианы треугольника пересекаются в одной точке,
вершины.
(центр тяжести треугольника – центроид)
Слайд 16Четвёртая замечательная точка
треугольника
Теорема. Высоты треугольника или их продолжения пересекаются в
точке(ортоцентр).