- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Пирамида по математике, основные свойства, площадь поверхности и объем
Содержание
- 1. Презентация Пирамида по математике, основные свойства, площадь поверхности и объем
- 2. а) основание пирамиды;б) высоту;в) апофему;г) диагональное сечение;д)
- 3. Дано: SABCD – пирамида, ABCD – квадрат,
- 4. Дано: SABCD – пирамида, ABCD – квадрат,
- 5. Дано: SABCD – пирамида, ABCD – ромб,
- 6. Дано: SABCD – пирамида, ABCD – ромб,
- 7. 1. Дано: SABCD – пирамида, ABCD –
- 8. В правильной треугольной пирамиде сторона основания равна
- 9. В правильной треугольной пирамиде сторона основания равна
- 10. В правильной четырехугольной пирамиде сторона основания равна
- 11. В правильной четырехугольной пирамиде сторона основания равна
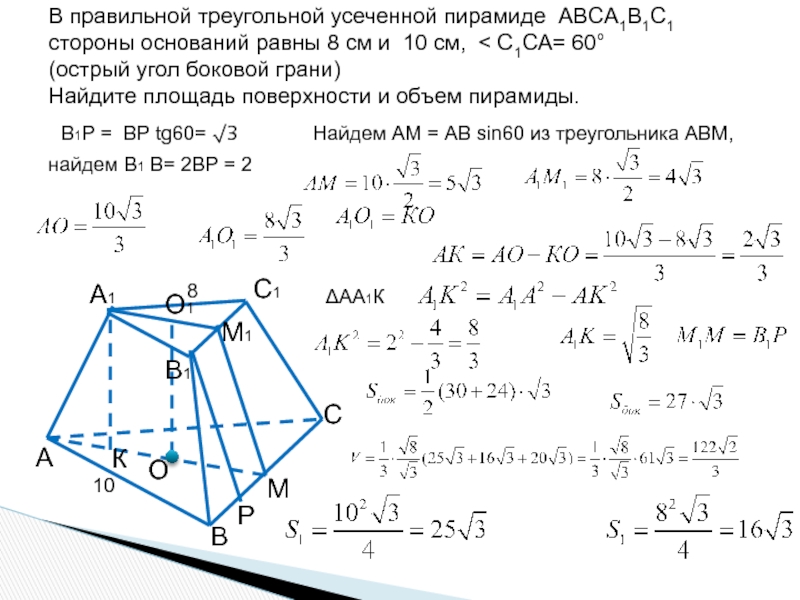
- 12. В правильной треугольной усеченной пирамиде ABCA1B1C1 стороны
- 13. В правильной треугольной усеченной пирамиде ABCA1B1C1 стороны
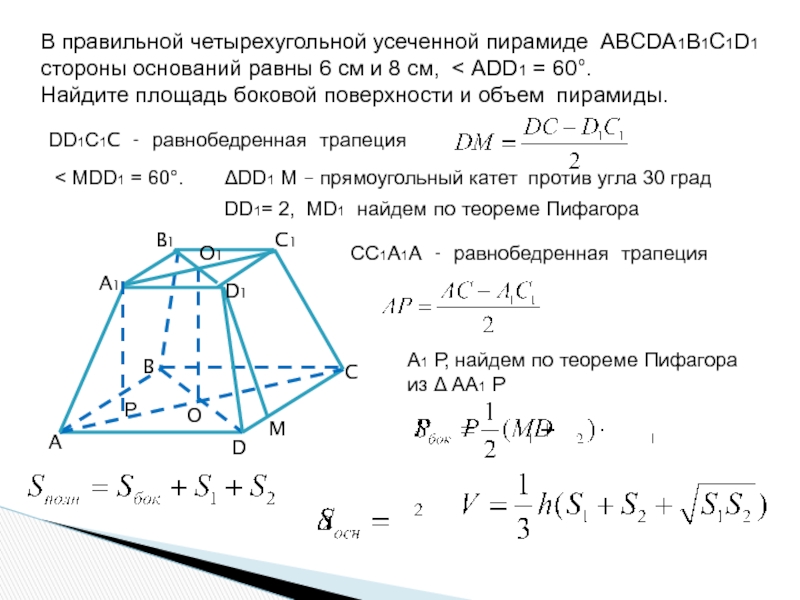
- 14. В правильной четырехугольной усеченной пирамиде ABCDA1B1C1D1 стороны
- 15. В правильной четырехугольной усеченной пирамиде ABCDA1B1C1D1 стороны
- 16. 2. В правильной треугольной усеченной пирамиде ABCA1B1C1
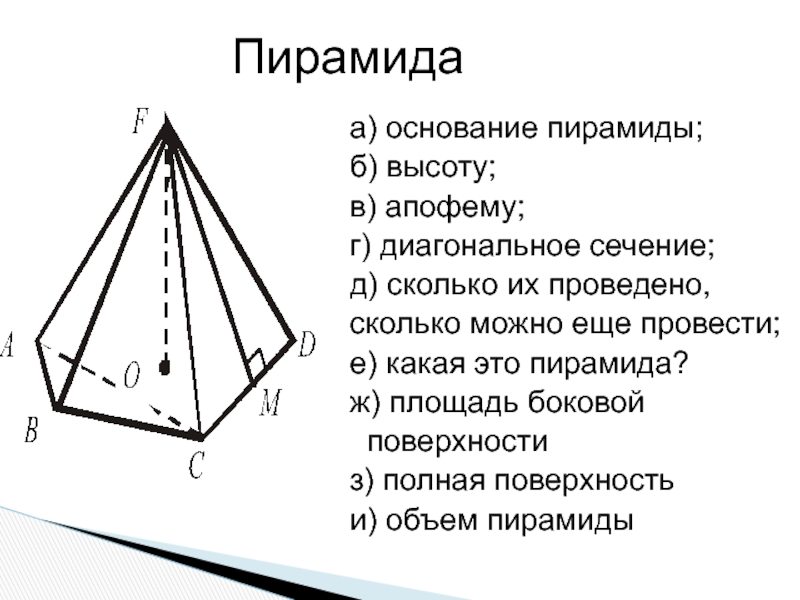
Слайд 2а) основание пирамиды;
б) высоту;
в) апофему;
г) диагональное сечение;
д) сколько их проведено,
сколько
е) какая это пирамида?
ж) площадь боковой
поверхности
з) полная поверхность
и) объем пирамиды
Пирамида
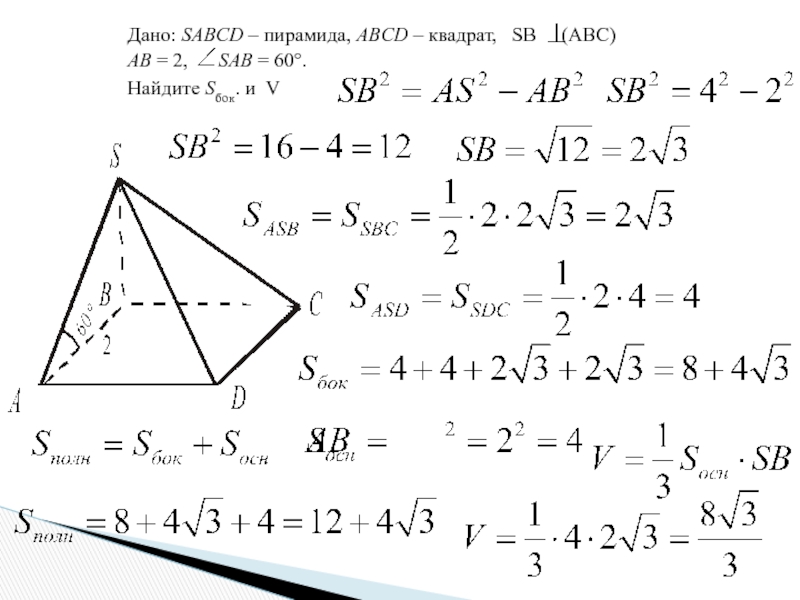
Слайд 3Дано: SABCD – пирамида, ABCD – квадрат, SB
АВ = 2, SAB = 60°.
Найдите Sполн и V
△ABS, прямоугольный, ∠ ASB = 30° ⇨ AS = 4
Найдем BS, высоту пирамиды, по теореме Пифагора
△ABS = △BSС, △DSС = △DSA
△DSС = △DSA, прямоугольные SA⊥ DA,
по теореме о трех перпендикулярах
Найдем площади граней как половину
произведения катетов.
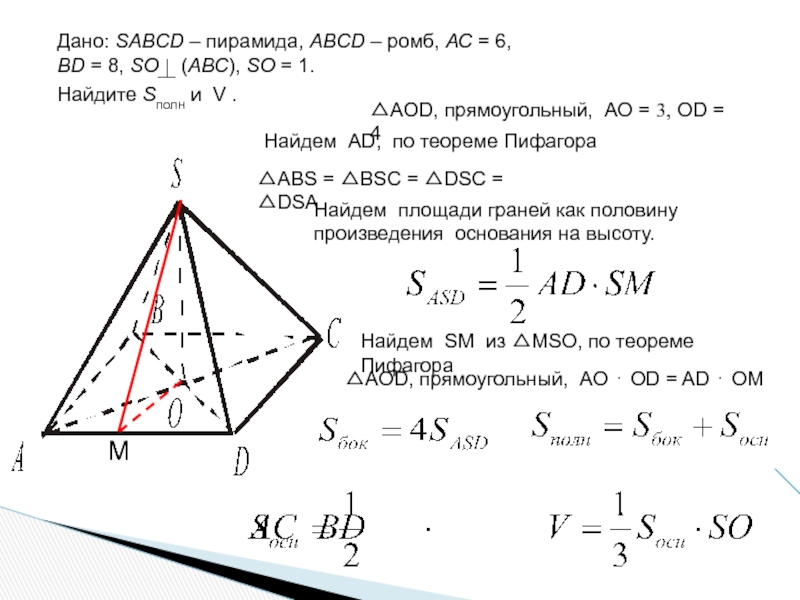
Слайд 5Дано: SABCD – пирамида, ABCD – ромб, АС = 6,
BD
Найдите Sполн и V .
△AOD, прямоугольный, AO = 3, OD = 4
Найдем AD, по теореме Пифагора
△ABS = △BSС = △DSС = △DSA
Найдем площади граней как половину
произведения основания на высоту.
М
Найдем SM из △МSО, по теореме Пифагора
△AOD, прямоугольный, AO ⋅ OD = AD ⋅ OМ
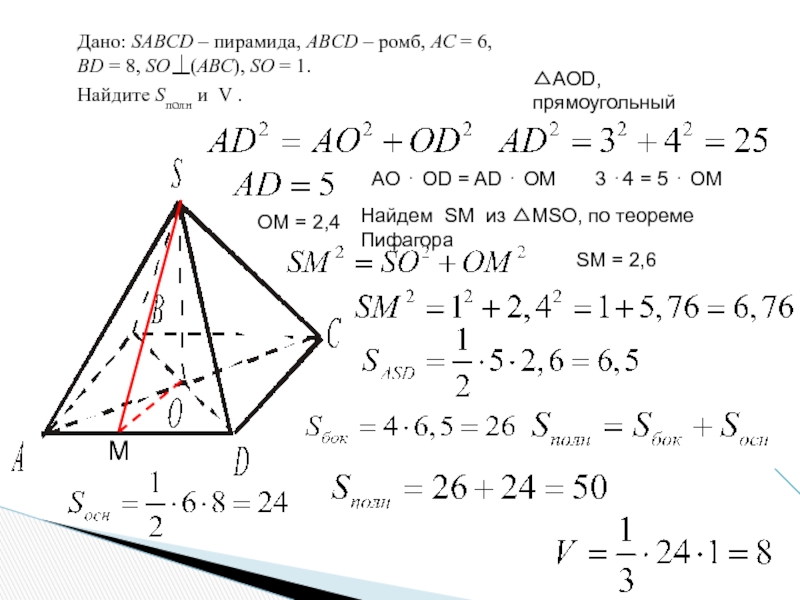
Слайд 6Дано: SABCD – пирамида, ABCD – ромб, АС = 6,
BD
Найдите Sполн и V .
М
Найдем SM из △МSО, по теореме Пифагора
△AOD, прямоугольный
AO ⋅ OD = AD ⋅ OМ
3 ⋅4 = 5 ⋅ OМ
OМ = 2,4
SМ = 2,6
Слайд 71. Дано: SABCD – пирамида, ABCD – квадрат, SB ⊥
АВ = 4, SAB = 45°.
Найдите Sполн и V
1. Дано: SABCD – пирамида, ABCD – квадрат, SB ⊥(ABC)
АВ = 6, SAB = 45°.
Найдите Sполн и V
2. Дано: SABCD – пирамида, ABCD – ромб, АС = 12, BD = 16, SO ⊥ (АВС), SO = 0,7.
Найдите Sполн и V .
2. Дано: SABCD – пирамида, ABCD – ромб, АС = 24, BD = 18, SO ⊥ (АВС), SO = 3.
Найдите Sполн и V .
Самостоятельная работа
Вариант1
Вариант2
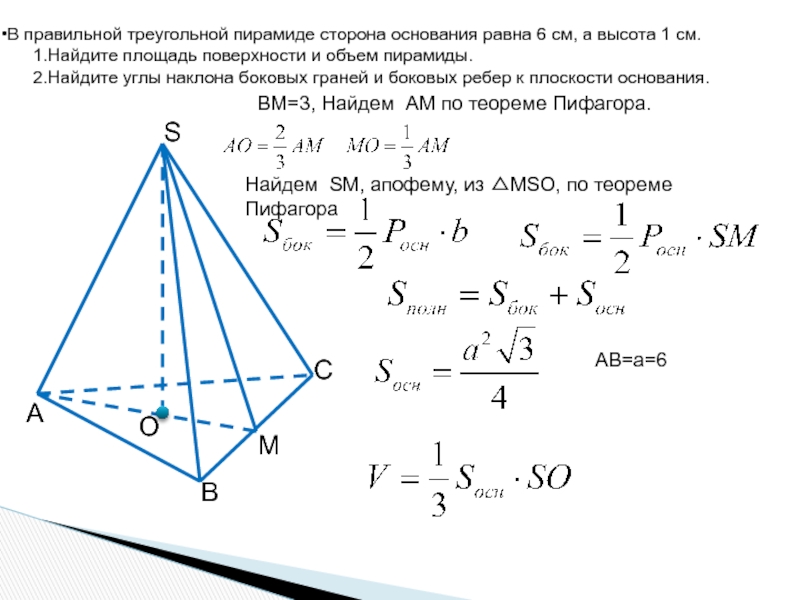
Слайд 8В правильной треугольной пирамиде сторона основания равна 6 см, а высота
Найдите площадь поверхности и объем пирамиды.
Найдите углы наклона боковых граней и боковых ребер к плоскости основания.
BM=3, Найдем АМ по теореме Пифагора.
Найдем SM, апофему, из △МSО, по теореме Пифагора
АB=a=6
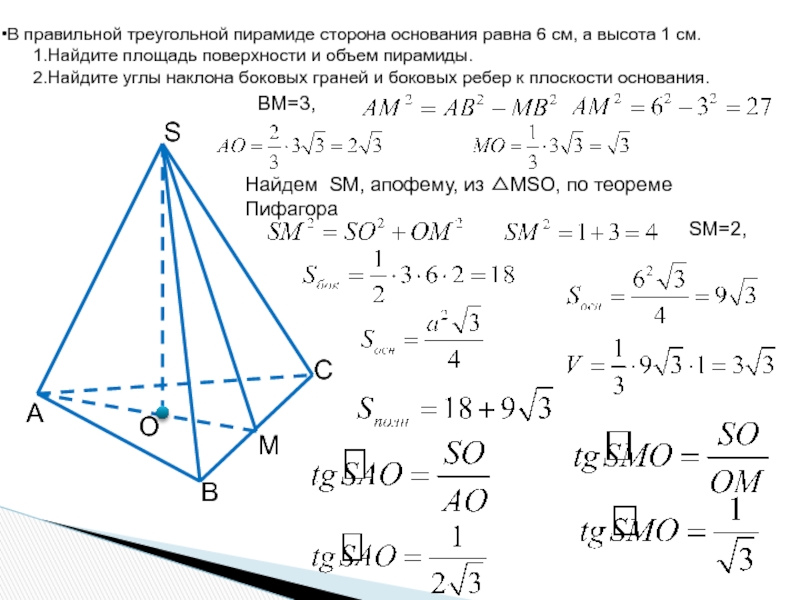
Слайд 9В правильной треугольной пирамиде сторона основания равна 6 см, а высота
Найдите площадь поверхности и объем пирамиды.
Найдите углы наклона боковых граней и боковых ребер к плоскости основания.
BM=3,
Найдем SM, апофему, из △МSО, по теореме Пифагора
SM=2,
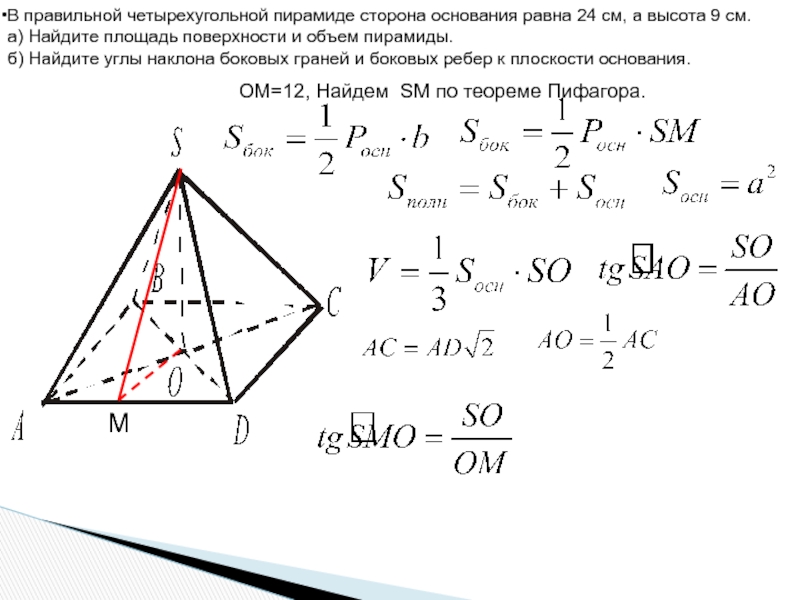
Слайд 10В правильной четырехугольной пирамиде сторона основания равна 24 см, а высота
а) Найдите площадь поверхности и объем пирамиды.
б) Найдите углы наклона боковых граней и боковых ребер к плоскости основания.
М
ОM=12, Найдем SМ по теореме Пифагора.
Слайд 11В правильной четырехугольной пирамиде сторона основания равна 24 см, а высота
а) Найдите площадь поверхности и объем пирамиды.
б) Найдите углы наклона боковых граней и боковых ребер к плоскости основания.
М
ОM=12, Найдем SМ по теореме Пифагора.
SM=15
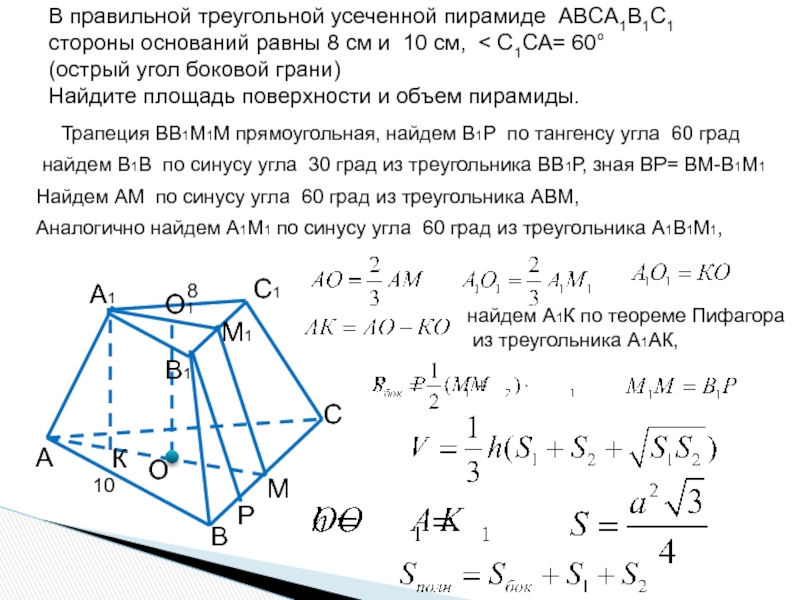
Слайд 12В правильной треугольной усеченной пирамиде ABCA1B1C1
стороны оснований равны 8 см
(острый угол боковой грани)
Найдите площадь поверхности и объем пирамиды.
10
8
Р
К
Трапеция ВВ1М1М прямоугольная, найдем В1Р по тангенсу угла 60 град
найдем В1В по синусу угла 30 град из треугольника ВВ1Р, зная ВР= ВМ-В1М1
Найдем АМ по синусу угла 60 град из треугольника АВМ,
Аналогично найдем А1М1 по синусу угла 60 град из треугольника А1В1М1,
найдем А1К по теореме Пифагора
из треугольника А1АК,
Слайд 13В правильной треугольной усеченной пирамиде ABCA1B1C1
стороны оснований равны 8 см
(острый угол боковой грани)
Найдите площадь поверхности и объем пирамиды.
10
8
Р
К
В1Р = ВР tg60= √3
найдем В1 B= 2ВР = 2
Найдем АМ = АВ sin60 из треугольника АВМ,
ΔAА1К
Слайд 14В правильной четырехугольной усеченной пирамиде ABCDA1B1C1D1
стороны оснований равны 6 см
Найдите площадь боковой поверхности и объем пирамиды.
A
DD1C1C - равнобедренная трапеция
B
C
D
O
M
A1
C1
O1
D1
B1
< MDD1 = 60°.
ΔDD1 M – прямоугольный катет против угла 30 град
DD1= 2, МD1 найдем по теореме Пифагора
СС1A1A - равнобедренная трапеция
Р
А1 Р, найдем по теореме Пифагора
из Δ АА1 Р
Слайд 15В правильной четырехугольной усеченной пирамиде ABCDA1B1C1D1
стороны оснований равны 6 см
Найдите площадь боковой поверхности и объем пирамиды.
A
DD1C1C - равнобедренная трапеция
B
C
D
O
M
A1
C1
O1
D1
B1
< MDD1 = 60°.
ΔDD1 M - прямоугольный DD1 = 2
МD1 по теореме Пифагора
СС1A1A - равнобедренная трапеция
Р
А1 Р, найдем по теореме Пифагора из Δ АА1Р
Слайд 162. В правильной треугольной усеченной пирамиде ABCA1B1C1
стороны оснований равны 6
(острый угол боковой грани)
Найдите площадь поверхности и объем пирамиды.
Вариант1
Вариант2
1. В правильной треугольной усеченной пирамиде ABCA1B1C1
стороны оснований равны 5 см и 9 см, < С1СА= 60°
(острый угол боковой грани)
Найдите площадь поверхности и объем пирамиды.
1. В правильной четырехугольной усеченной пирамиде ABCDA1B1C1D1 стороны оснований равны 3 см и 12 см, < ADD1 = 30°.
Найдите площадь поверхности и объем пирамиды.
2. В правильной четырехугольной усеченной пирамиде ABCDA1B1C1D1 стороны оснований равны 4 см и 10 см, < ADD1 = 30°.
Найдите площадь поверхности и объем пирамиды.
Самостоятельная работа