- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Метод координат в пространстве
Содержание
- 1. Презентация Метод координат в пространстве
- 2. Разложение вектора по трём некомпланарным векторампричем коэффициенты разложения x, y, z определяются единственным образом.
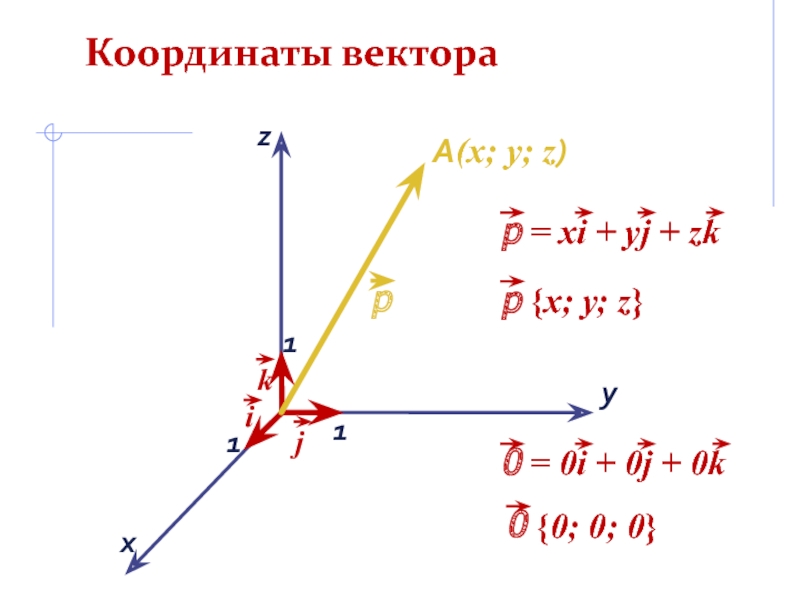
- 3. Координаты вектораxyA(x; y; z)111z
- 4. Действия над векторамиКаждая координата суммы двух или
- 5. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.Действия над векторами
- 6. Примеры Дано:Найти:Решение:++
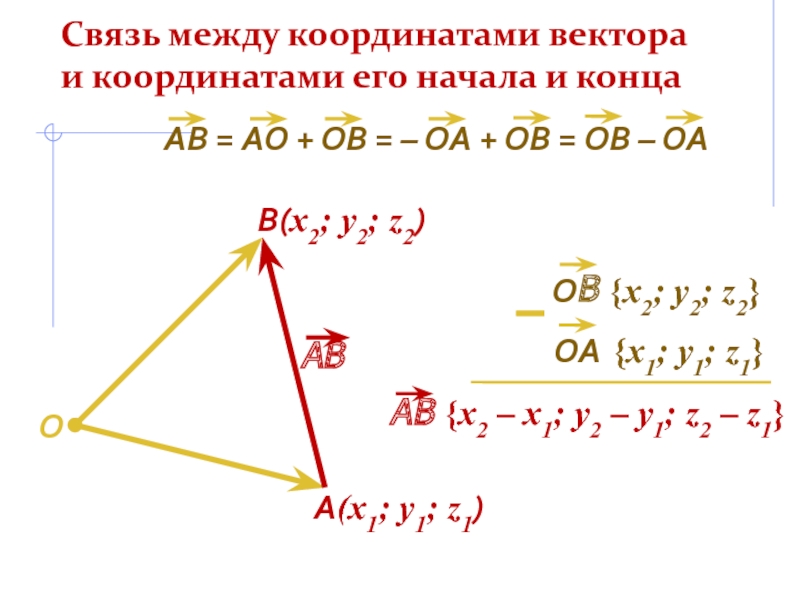
- 7. Связь между координатами вектора и координатами его начала и концаOA(x1; y1; z1)В(x2; y2; z2)–
- 8. Каждая координата вектора
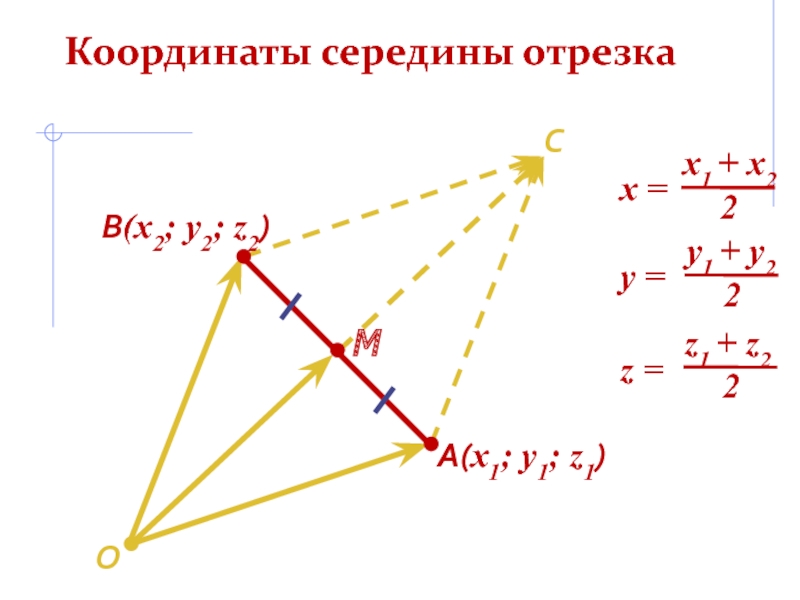
- 9. Координаты середины отрезкаМA(x1; y1; z1)В(x2; y2; z2)СO
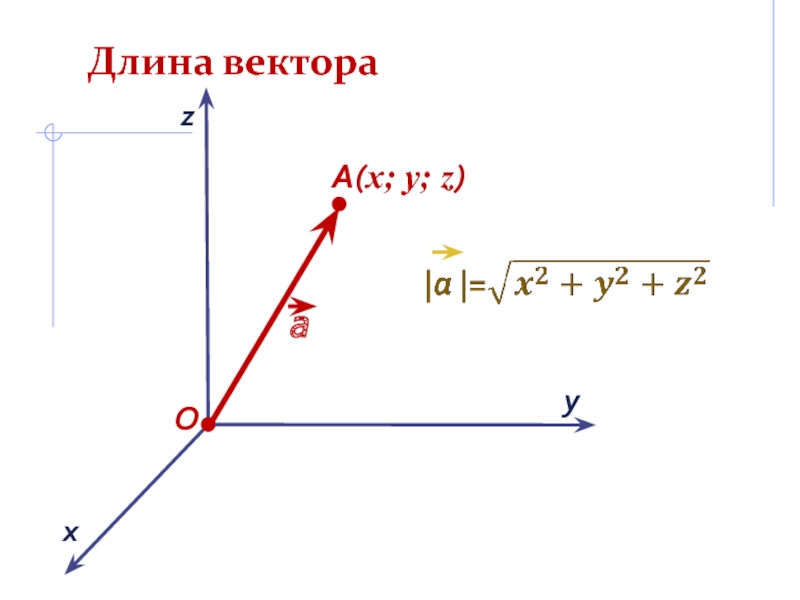
- 10. Длина вектораOxyA(x; y; z)z
- 11. Расстояние между двумя точкамиA(x1; y1; z1)В(x2; y2; z2)
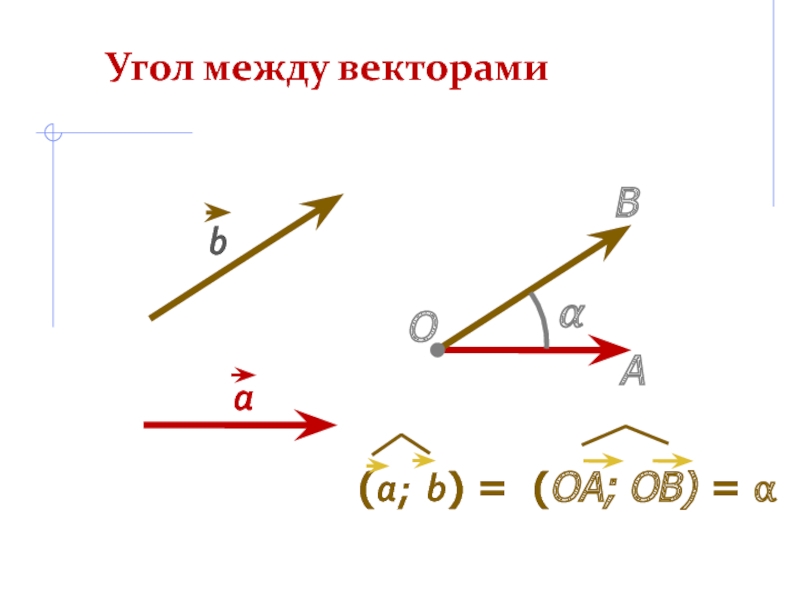
- 12. Угол между векторамиОАВα
- 13. Скалярное произведение векторовСкалярным произведением двух векторов называется
- 14. Скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату его длины.Скалярное произведение векторов
- 15. Скалярное произведение векторов
- 16. Свойства скалярного произведения векторов
- 17. Угол между прямыми
Разложение вектора по трём некомпланарным векторампричем коэффициенты разложения x, y, z определяются единственным образом.
Слайд 2Разложение вектора по трём некомпланарным векторам
причем коэффициенты разложения x, y, z
определяются единственным образом.
Слайд 4Действия над векторами
Каждая координата суммы двух или более векторов равна сумме
соответствующих координат этих векторов.
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Слайд 5Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора
на это число.
Действия над векторами
Слайд 7Связь между координатами вектора и координатами его начала и конца
O
A(x1; y1;
z1)
В(x2; y2; z2)
–
Слайд 8 Каждая координата вектора равна разности соответствующих координат
его конца и начала.
Примеры
А(5; 3; –4), В(–2; 4; 1)
M(–3; 8; 2), N(0; –6; 5)
Связь между координатами вектора и координатами его начала и конца
Слайд 13Скалярное произведение векторов
Скалярным произведением двух векторов называется произведение их длин на
косинус угла между ними.
Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
Слайд 14Скалярный квадрат вектора (т.е. скалярное произведение вектора на себя) равен квадрату
его длины.
Скалярное произведение векторов
