«А» класса
Феоктистова Екатерина
Панина Арина
Аверина Валерия
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к проекту: Симметрия в пространстве
Содержание
- 1. Презентация к проекту: Симметрия в пространстве
- 2. Что такое симметрия?Геометрическая симметрия — это наиболее известный
- 3. Виды симметрии2.Осевая симметрия1.Центральная симметрия 4.Поворотная симметрия 3.Зеркальная симметрия 5.Переносная симметрия
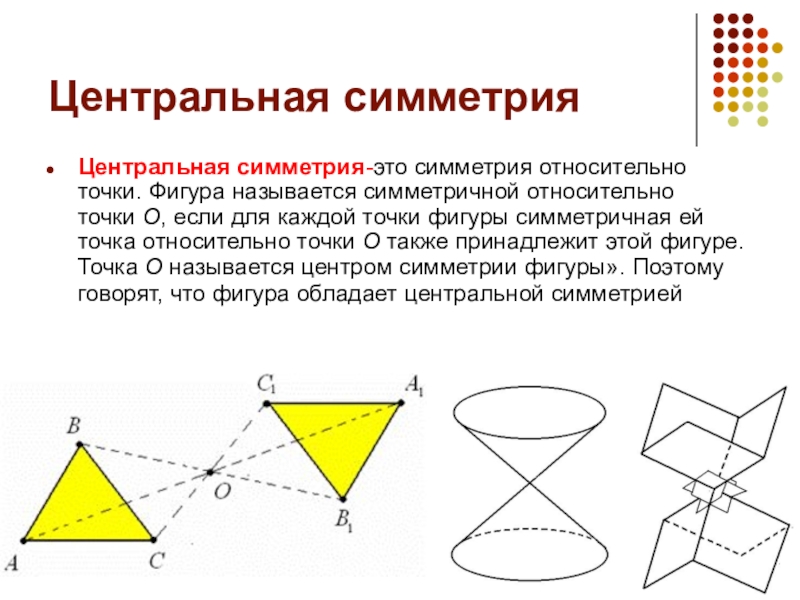
- 4. Центральная симметрияЦентральная симметрия-это симметрия относительно точки. Фигура
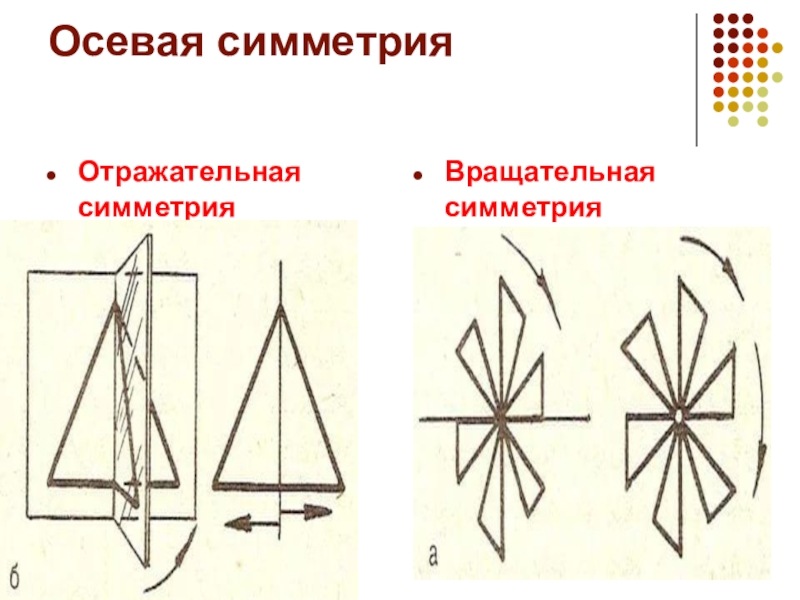
- 5. Осевая симметрия Осевая симметрия-это симметрия относительно прямой.
- 6. Осевая симметрияОтражательная симметрия Вращательная симметрия
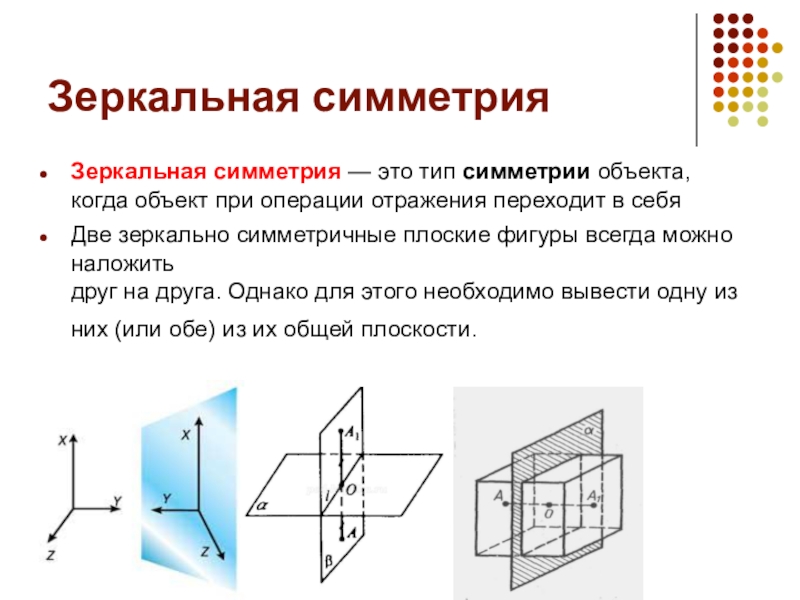
- 7. Зеркальная симметрияЗеркальная симметрия — это тип симметрии объекта, когда объект при
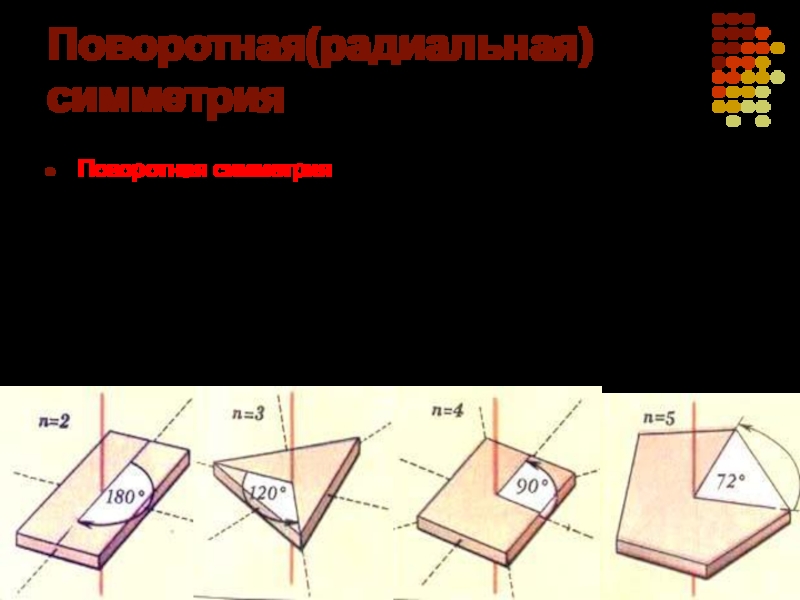
- 8. Поворотная(радиальная) симметрияПоворотная симметрия — это симметрия, сохраняющаяся форму
- 9. Переносная симметрияО такой симметрии говорят тогда, когда
- 10. ВыводТаким образом, существуют различные виды симметрии, симметричные
- 11. Слайд 11
Что такое симметрия?Геометрическая симметрия — это наиболее известный тип симметрии для многих людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если ее точки попарно обладают указанным свойством. Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.
Слайд 2Что такое симметрия?
Геометрическая симметрия — это наиболее известный тип симметрии для многих
людей. Геометрический объект называется симметричным, если после того как он был преобразован геометрически, он сохраняет некоторые исходные свойства
Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если ее точки попарно обладают указанным свойством. Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.
Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если ее точки попарно обладают указанным свойством. Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.
Слайд 3Виды симметрии
2.Осевая симметрия
1.Центральная симметрия
4.Поворотная симметрия
3.Зеркальная симметрия
5.Переносная симметрия
Слайд 4Центральная симметрия
Центральная симметрия-это симметрия относительно точки. Фигура называется симметричной относительно точки О, если
для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры». Поэтому говорят, что фигура обладает центральной симметрией
Слайд 5Осевая симметрия
Осевая симметрия-это симметрия относительно прямой. Она имеет 2 определения:
Отражательная симметрия - вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но, например, конус будет.
Слайд 7Зеркальная симметрия
Зеркальная симметрия — это тип симметрии объекта, когда объект при операции отражения переходит в
себя
Две зеркально симметричные плоские фигуры всегда можно наложить друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости.
Две зеркально симметричные плоские фигуры всегда можно наложить друг на друга. Однако для этого необходимо вывести одну из них (или обе) из их общей плоскости.
Слайд 8Поворотная(радиальная) симметрия
Поворотная симметрия — это симметрия, сохраняющаяся форму предмета при повороте вокруг некоторой
оси на угол, равный 360°/n (или кратный этой величине), где n = 2, 3, 4, … Указанную ось называют поворотной осью n-го порядка. При п=2 все точки фигуры поворачиваются на угол 180(360 /2 = 180)вокруг оси, при этом форма фигуры сохраняется, т.е. каждая точка фигуры переходит в точку той же фигуры(фигура преобразуется сама в себя).
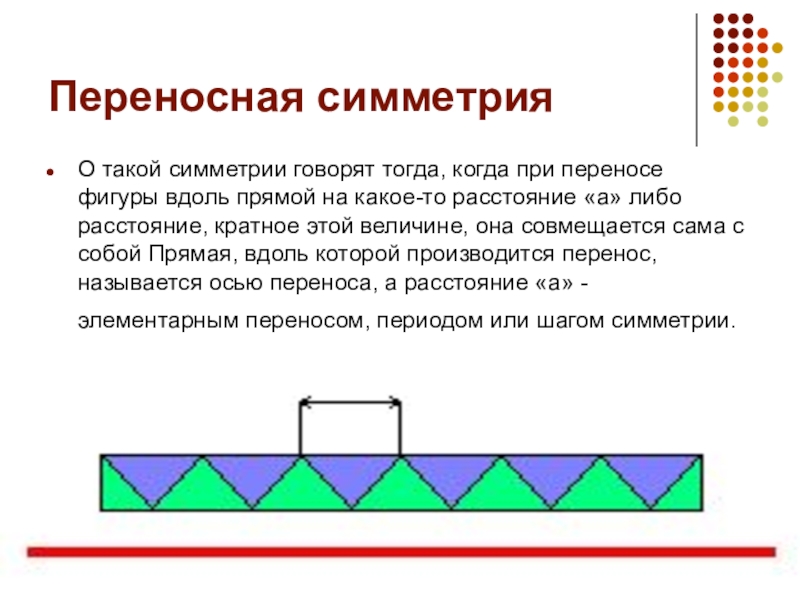
Слайд 9Переносная симметрия
О такой симметрии говорят тогда, когда при переносе фигуры вдоль
прямой на какое-то расстояние «а» либо расстояние, кратное этой величине, она совмещается сама с собой Прямая, вдоль которой производится перенос, называется осью переноса, а расстояние «а» - элементарным переносом, периодом или шагом симметрии.
Слайд 10Вывод
Таким образом, существуют различные виды симметрии, симметричные точки в каждом из
этих видов симметрии строятся по определённым законам.
В заключении хочется сказать о том, что быть прекрасным значит быть симметричным и соразмерным.
В заключении хочется сказать о том, что быть прекрасным значит быть симметричным и соразмерным.