- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема Пифагора (8 класс, геометрия)
Содержание
- 1. Теорема Пифагора (8 класс, геометрия)
- 2. Телекомпания «Sirotkin Productions» представляет
- 3. Фильм из серии «Геометрия. 8 класс»
- 4. Теорема Пифагора
- 5. Теорема Пифагора устанавливает простую зависимость между сторонами прямоугольного треугольника.ABCКатетКатетГипотенуза
- 6. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.caba2 + b2 = c2Теорема Пифагора
- 7. Немного истории… Наиболее известный частный случай
- 8. Треугольник со сторонами 3, 4 и 5
- 9. Немного истории…Древнегреческий математик Пифагор в 540 г. до н.э. дал первое логически стройное доказательство этому соотношению.
- 10. Доказать теорему Пифагора можнонесколькими сотнями способов. Она
- 11. Площадь квадрата построенного на гипотенузе равна сумме площадей квадратов построенных на катетахДоказательство теоремы ПифагораДоказательство Евклида
- 12. Квадраты дополняются до равных фигур равными же фигурамиДоказательство теоремы ПифагораДоказательство Леонардо да Винчи
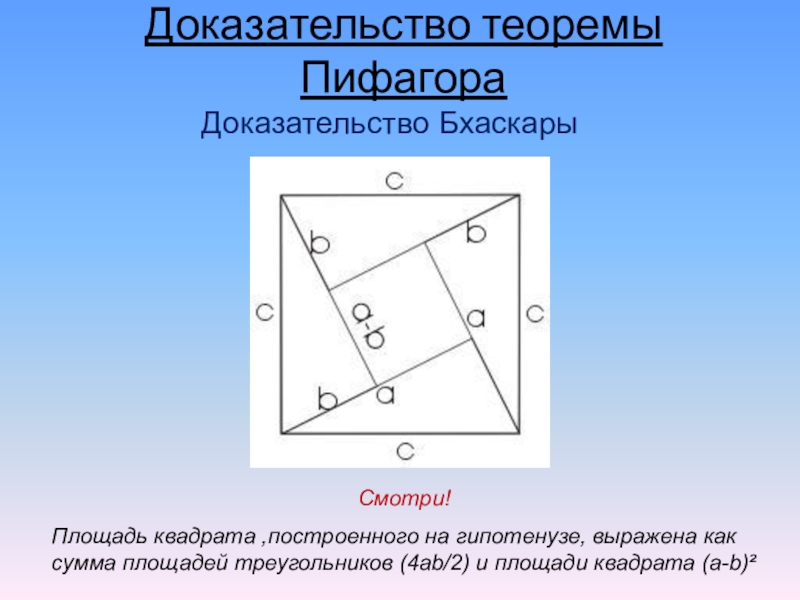
- 13. Доказательство теоремы ПифагораДоказательство БхаскарыСмотри!Площадь квадрата ,построенного на
- 14. Доказательство теоремы ПифагораДоказательство с использованием подобия треугольниковabcSaSbSa
- 15. Теорема, обратная к теореме Пифагора
- 16. Значение теоремы Пифагора Теорема Пифагора позволяет
- 17. «…И теорема Пифагора Через столько лет
- 18. Разработал и выполнил Сироткин Виталий 8 «К» класс
Телекомпания «Sirotkin Productions» представляет
Слайд 1 Из всех прочих известных нам наук, только арифметика и геометрия чисты
от всякого ложного и недостоверного
Рене Декарт.
Слайд 5
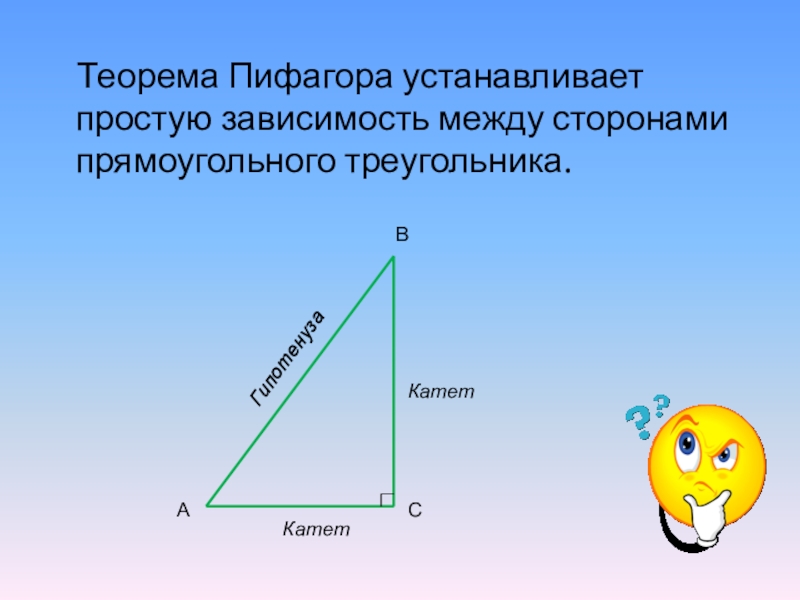
Теорема Пифагора устанавливает простую зависимость между сторонами прямоугольного треугольника.
A
B
C
Катет
Катет
Гипотенуза
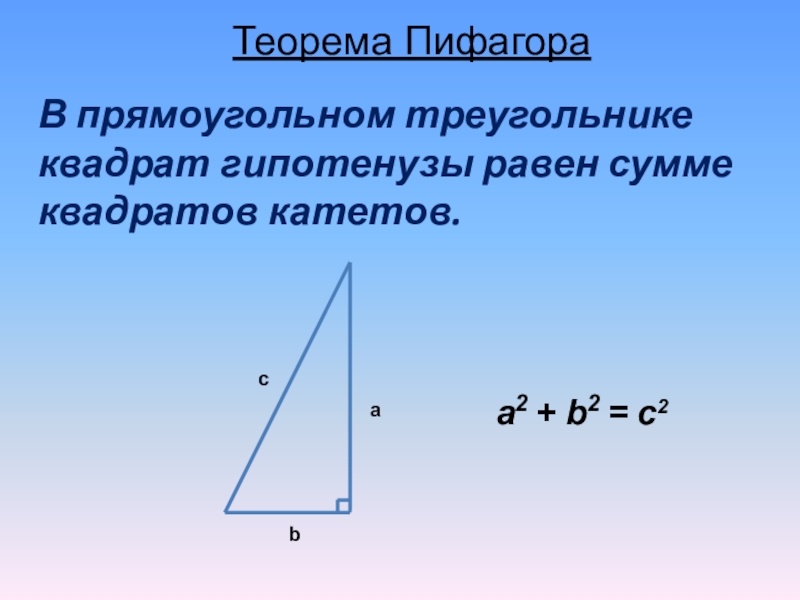
Слайд 6 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
c
a
b
a2
+ b2 = c2
Теорема Пифагора
Слайд 7Немного истории…
Наиболее известный частный случай теоремы – египетский треугольник
со сторонами 3, 4 и 5
3
4
5
32 + 42 = 52
Это было установлено в 2000 г до нашей эры
Слайд 8Треугольник со сторонами 3, 4 и 5 был
известен в древнем Китае:
«Если
прямой угол разложить на составные
части, то линия, соединяющая концы его
сторон, будет 5, когда основание есть 3, а
высота 4»
части, то линия, соединяющая концы его
сторон, будет 5, когда основание есть 3, а
высота 4»
Немного истории…
3
4
5
Слайд 9Немного истории…
Древнегреческий математик Пифагор в 540 г. до н.э. дал первое
логически стройное доказательство этому соотношению.
Слайд 10Доказать теорему Пифагора можно
несколькими сотнями способов. Она даже
попала в книгу рекордов
Гиннесса. Но самым
известных доказательств – четыре.
известных доказательств – четыре.
Доказательство теоремы Пифагора
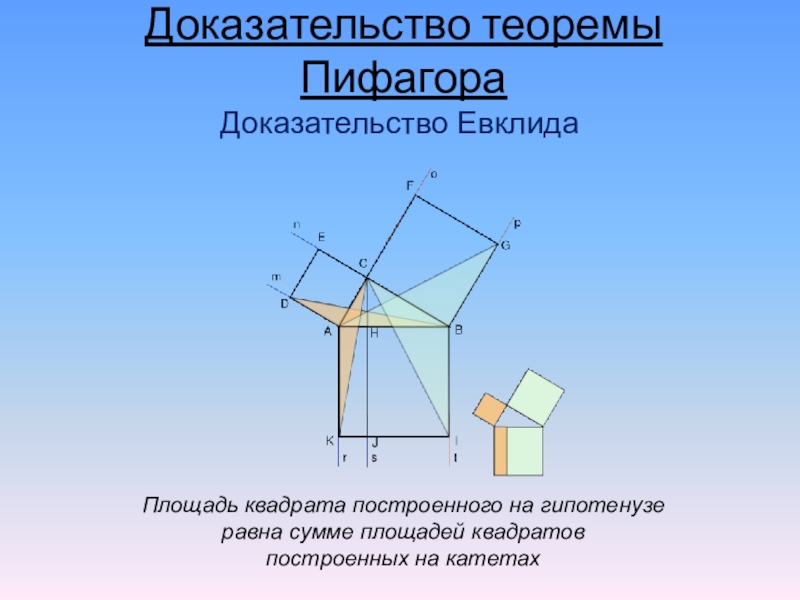
Слайд 11Площадь квадрата построенного на гипотенузе
равна сумме площадей квадратов
построенных на
катетах
Доказательство теоремы Пифагора
Доказательство Евклида
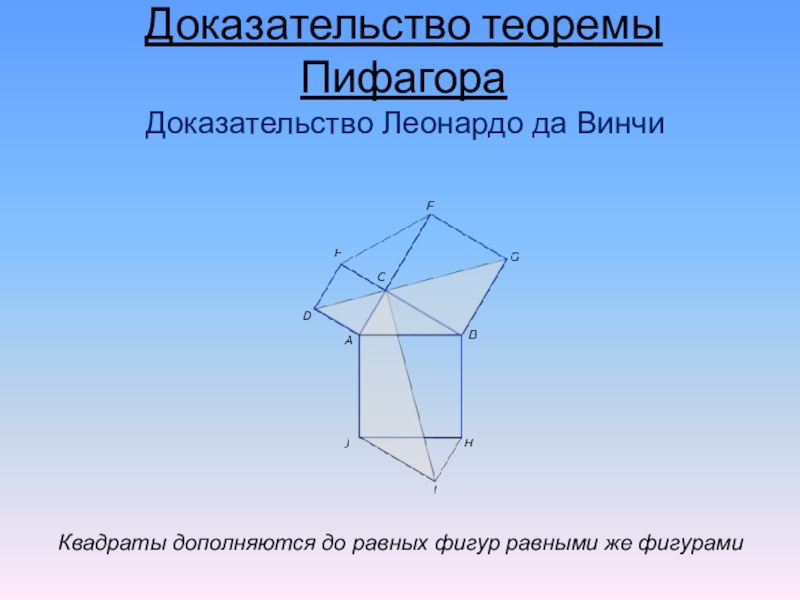
Слайд 12Квадраты дополняются до равных фигур равными же фигурами
Доказательство теоремы Пифагора
Доказательство Леонардо
да Винчи
Слайд 13Доказательство теоремы Пифагора
Доказательство Бхаскары
Смотри!
Площадь квадрата ,построенного на гипотенузе, выражена как сумма
площадей треугольников (4ab/2) и площади квадрата (a-b)²
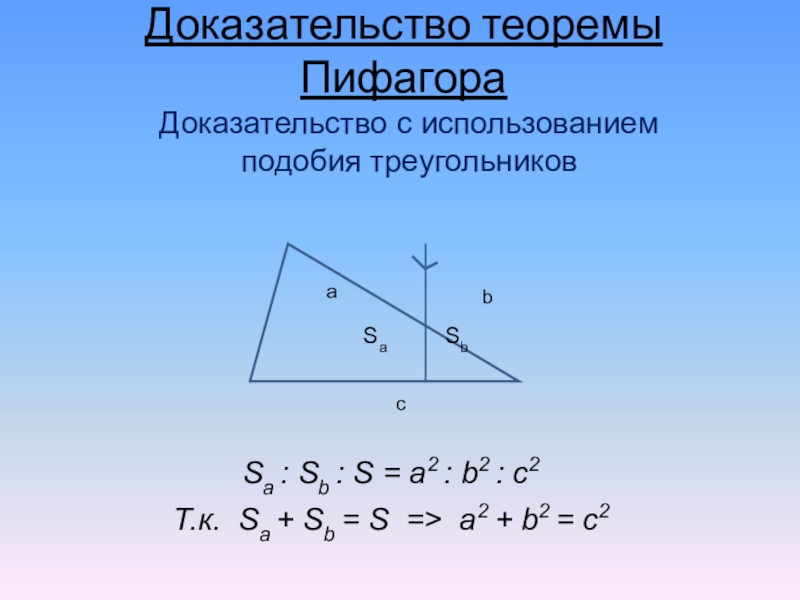
Слайд 14Доказательство теоремы Пифагора
Доказательство с использованием подобия треугольников
a
b
c
Sa
Sb
Sa : Sb : S
= a2 : b2 : c2
Т.к. Sa + Sb = S => a2 + b2 = c2
Т.к. Sa + Sb = S => a2 + b2 = c2
Слайд 15Теорема, обратная к теореме Пифагора
Если стороны
треугольника удовлетворяют равенству a2 + b2 = c2, то этот треугольник прямоугольный
a
b
c
90o
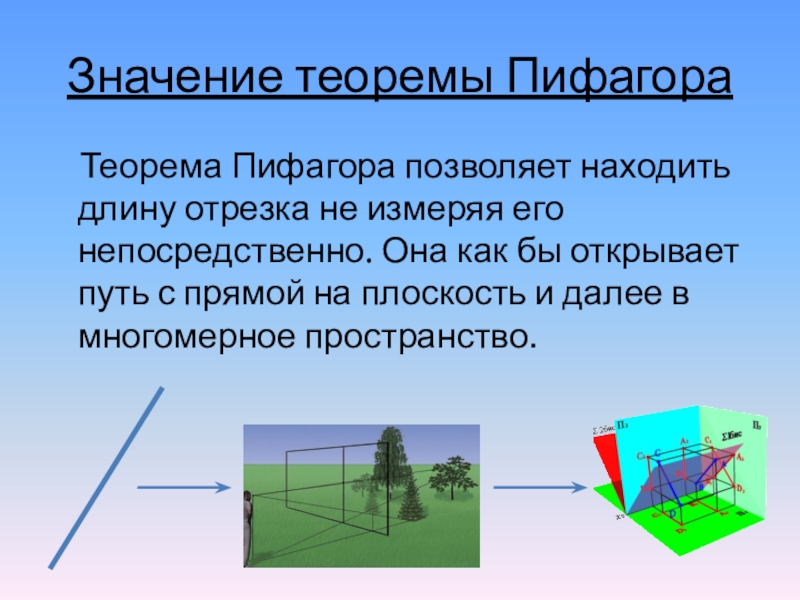
Слайд 16Значение теоремы Пифагора
Теорема Пифагора позволяет находить длину отрезка не
измеряя его непосредственно. Она как бы открывает путь с прямой на плоскость и далее в многомерное пространство.
Слайд 17«…И теорема Пифагора Через столько лет Для нас как для него Бесспорна, безупречна.»
Альберт фон Шамиссо