- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Изображение пространственных фигур (10 класс)
Содержание
- 1. Презентация Изображение пространственных фигур (10 класс)
- 2. Ответьте на вопросы 1. Верно ли, что через
- 3. Ответ: Неверно. По теореме о существовании
- 4. Ответьте на вопросы 2. Верно ли, что если
- 5. Ответ: Верно. По лемме о пересечении плоскости двумя
- 6. Ответьте на вопросы 3. Верно ли, что две непересекающиеся прямые в пространстве параллельны?
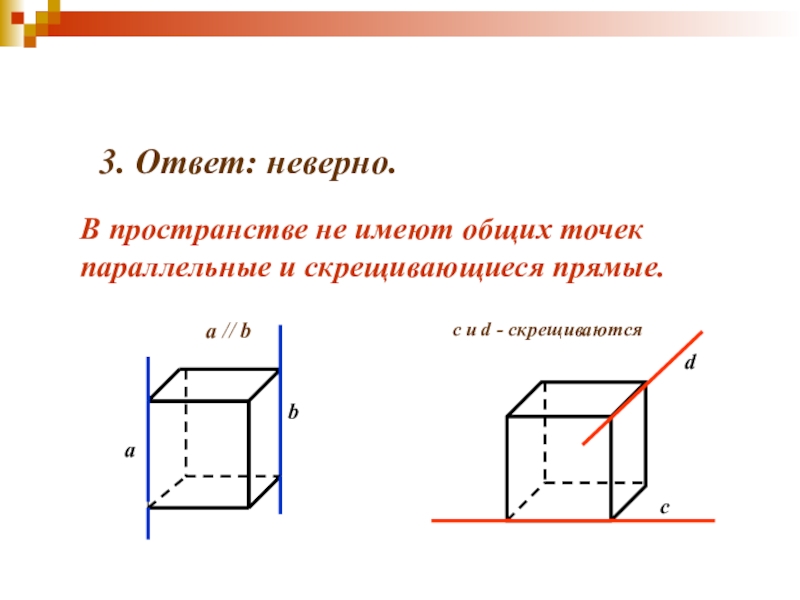
- 7. сdc и d - скрещиваются3. Ответ: неверно.В пространстве не имеют общих точек параллельные и скрещивающиеся прямые.
- 8. Ответьте на вопросы 4. Верно ли, что если
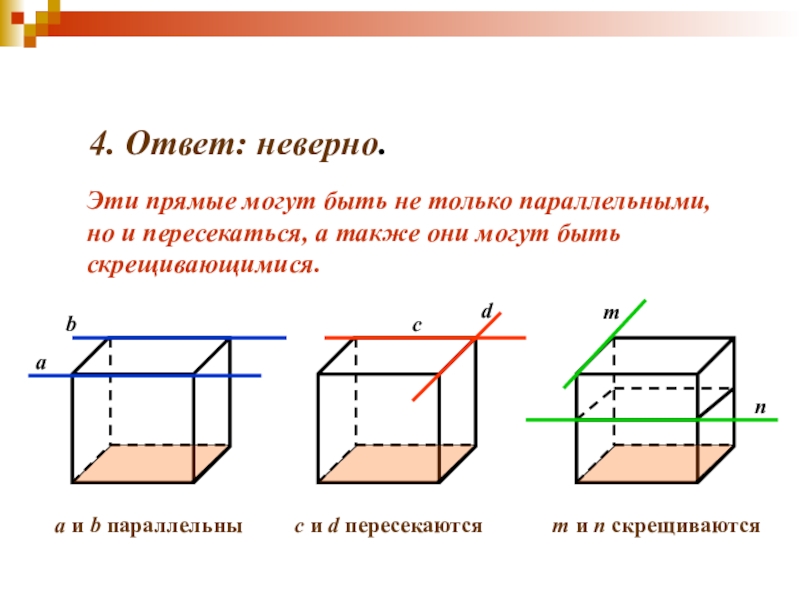
- 9. 4. Ответ: неверно.Эти прямые могут быть не
- 10. Изображения пространственных фигур
- 11. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ1. Проекция точки есть точка.2. Проекция прямой есть прямая.A0AanA’lBCAB’C’
- 12. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ3. Проекция отрезка есть отрезок.4.
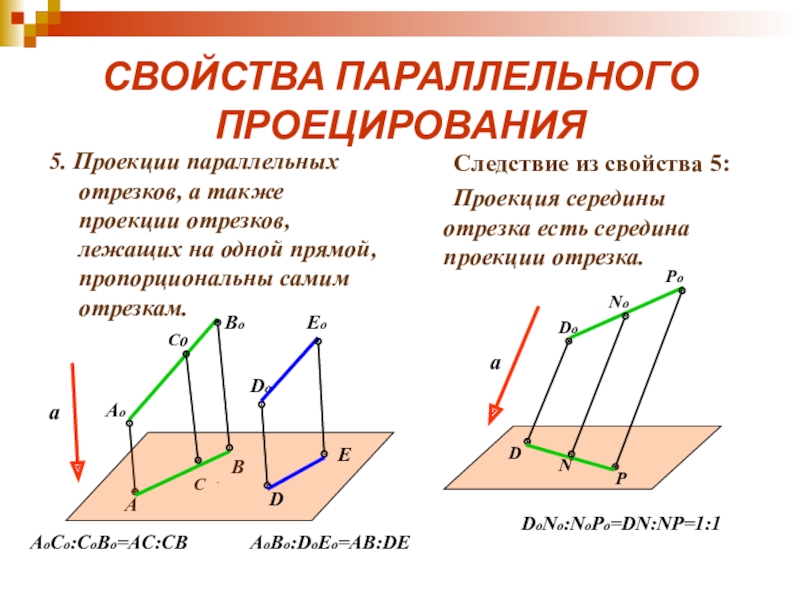
- 13. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ5. Проекции параллельных отрезков, а
- 14. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯПри параллельном проецировании сохраняются следующие
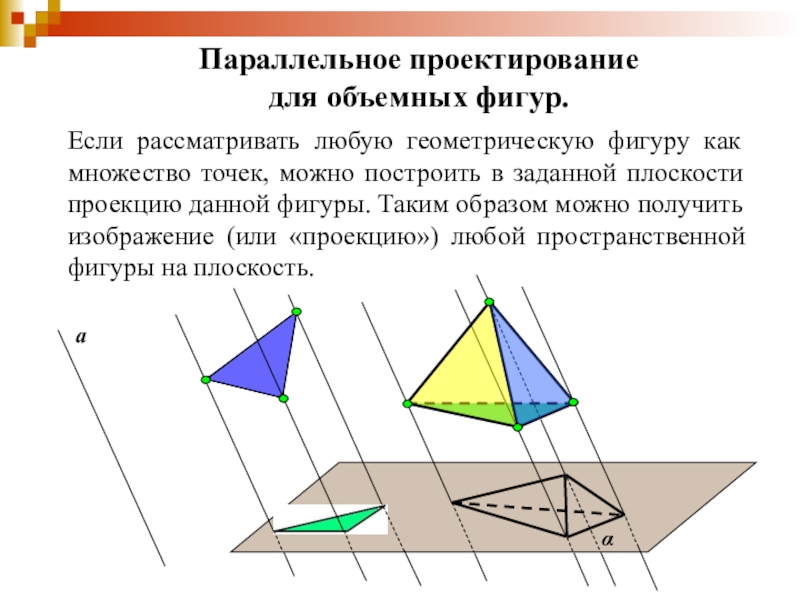
- 15. Параллельное проектирование для объемных фигур.Если рассматривать любую
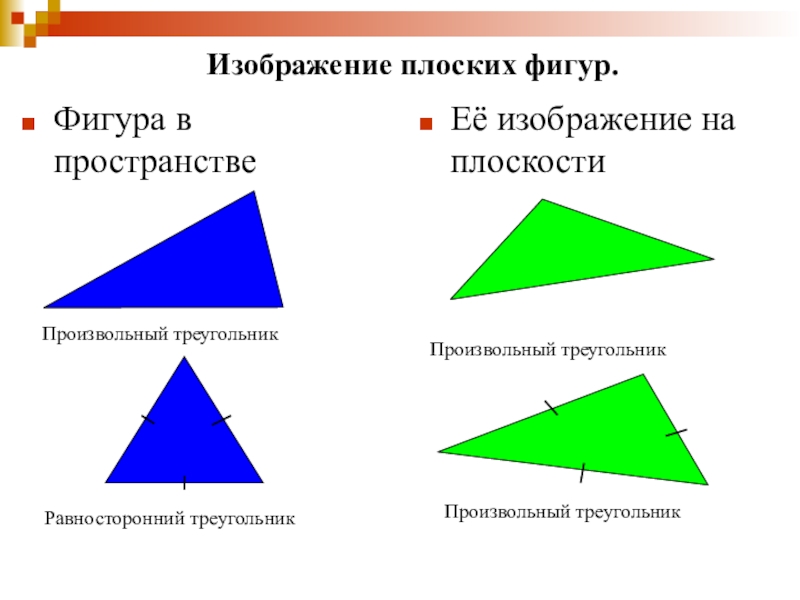
- 16. Изображение плоских фигур.Фигура в пространствеЕё изображение на плоскостиПроизвольный треугольникПроизвольный треугольникРавносторонний треугольникПроизвольный треугольник
- 17. Фигура в пространствеЕё изображение на плоскостиПрямоугольный треугольникРавнобедренный треугольникПроизвольный треугольникПроизвольный треугольник
- 18. Фигура в пространствеЕё изображение на плоскостиПараллелограммПрямоугольникПроизвольный параллелограммПроизвольный параллелограммКругОвал (эллипс)
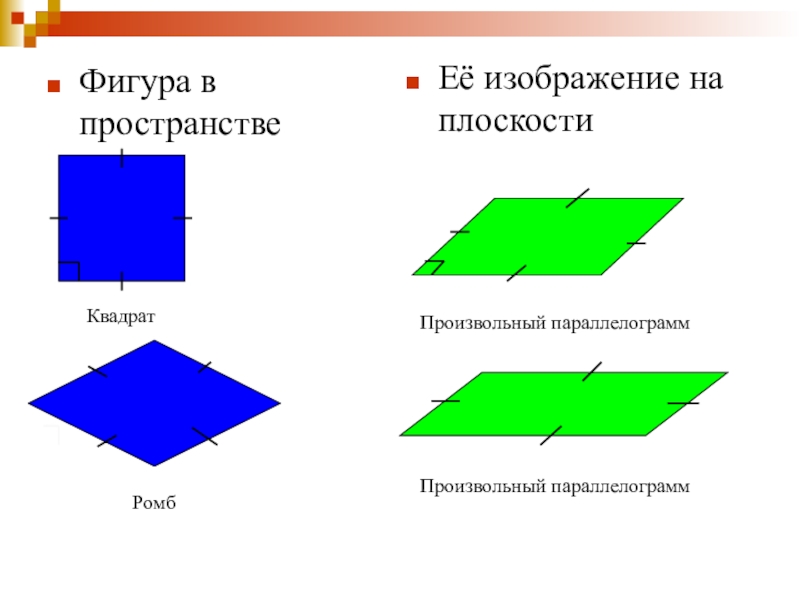
- 19. Фигура в пространствеЕё изображение на плоскостиКвадратРомбПроизвольный параллелограммПроизвольный параллелограмм
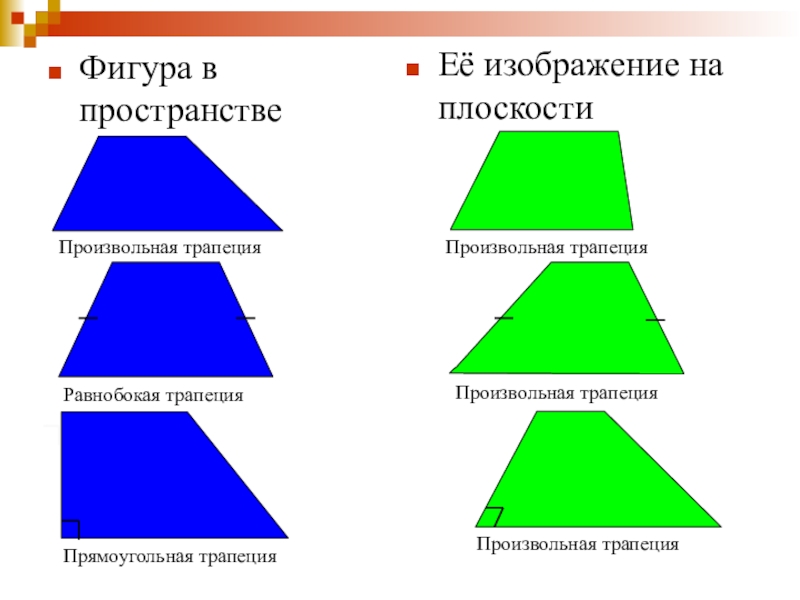
- 20. Фигура в пространствеЕё изображение на плоскостиПроизвольная трапецияПроизвольная трапецияРавнобокая трапецияПрямоугольная трапецияПроизвольная трапецияПроизвольная трапеция
- 21. Алгоритм построения изображения пирамиды.1. Изображение пирамиды начинают
- 22. Задача №1Построить изображение пирамиды в основании которой
- 23. 3. Построение боковых ребер:Вершины верхней грани призмы
- 24. Задача №2Построить изображение призмы в основании которой
Слайд 2Ответьте на вопросы
1. Верно ли, что через любую точку пространства можно
Слайд 3 Ответ: Неверно.
По теореме о существовании прямой, параллельной данной прямой,
Слайд 4Ответьте на вопросы
2. Верно ли, что если одна из двух параллельных
Слайд 5 Ответ: Верно.
По лемме о пересечении плоскости двумя параллельными прямыми, если одна
b
a
M
Слайд 7с
d
c и d - скрещиваются
3. Ответ: неверно.
В пространстве не имеют общих
параллельные и скрещивающиеся прямые.
Слайд 8Ответьте на вопросы
4. Верно ли, что если две прямые параллельны некоторой
Слайд 9 4. Ответ: неверно.
Эти прямые могут быть не только параллельными,
но и
a
b
c
d
m
n
a и b параллельны
с и d пересекаются
m и n скрещиваются
Слайд 11СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ
1. Проекция точки есть точка.
2. Проекция прямой есть прямая.
A0
A
a
n
A’
l
B
C
A
B’
C’
Слайд 12СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕКТИРОВАНИЯ
3. Проекция отрезка есть отрезок.
4. Проекции параллельных отрезков –
a
Ao
Bo
A
B
l
A1
k1
A1’
B
A2
k2
A2’
k1’
Слайд 13СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
5. Проекции параллельных отрезков, а также проекции отрезков, лежащих
Следствие из свойства 5:
Проекция середины отрезка есть середина проекции отрезка.
a
Ao
Bo
A
B
Co
C
No
Do
Po
D
P
N
AoCo:CoBo=AC:CB
DoNo:NoPo=DN:NP=1:1
a
Do
Eo
D
E
AoBo:DoEo=AB:DE
Слайд 14СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
При параллельном проецировании сохраняются следующие свойства фигур
1. Свойство
плоскостью.
2. Свойство фигур иметь пересечение.
3. Деление отрезка в данном отношении.
4. Параллельность прямых и плоскостей.
5. Свойство фигуры быть треугольником, параллелограммом, трапецией.
6. Отношение длин параллельных отрезков.
7. Отношение площадей двух фигур.
Слайд 15Параллельное проектирование
для объемных фигур.
Если рассматривать любую геометрическую фигуру как множество
Слайд 16Изображение плоских фигур.
Фигура в пространстве
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Равносторонний треугольник
Произвольный
Слайд 17Фигура в пространстве
Её изображение на плоскости
Прямоугольный треугольник
Равнобедренный треугольник
Произвольный треугольник
Произвольный треугольник
Слайд 18Фигура в пространстве
Её изображение на плоскости
Параллелограмм
Прямоугольник
Произвольный параллелограмм
Произвольный параллелограмм
Круг
Овал (эллипс)
Слайд 19Фигура в пространстве
Её изображение на плоскости
Квадрат
Ромб
Произвольный параллелограмм
Произвольный параллелограмм
Слайд 20Фигура в пространстве
Её изображение на плоскости
Произвольная трапеция
Произвольная трапеция
Равнобокая трапеция
Прямоугольная трапеция
Произвольная трапеция
Произвольная
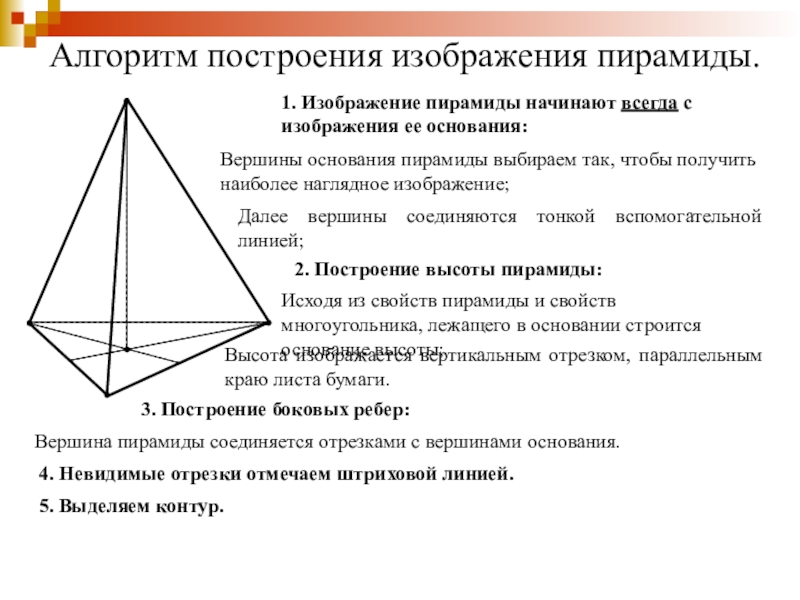
Слайд 21Алгоритм построения изображения пирамиды.
1. Изображение пирамиды начинают всегда с изображения ее
Вершины основания пирамиды выбираем так, чтобы получить наиболее наглядное изображение;
Далее вершины соединяются тонкой вспомогательной линией;
2. Построение высоты пирамиды:
Исходя из свойств пирамиды и свойств многоугольника, лежащего в основании строится основание высоты;
Высота изображается вертикальным отрезком, параллельным краю листа бумаги.
3. Построение боковых ребер:
Вершина пирамиды соединяется отрезками с вершинами основания.
4. Невидимые отрезки отмечаем штриховой линией.
5. Выделяем контур.
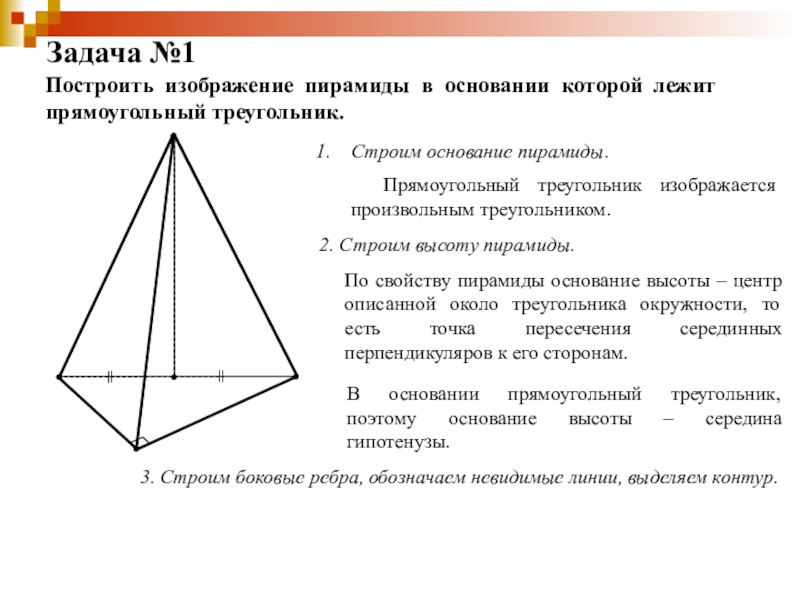
Слайд 22Задача №1
Построить изображение пирамиды в основании которой лежит прямоугольный треугольник.
Строим основание пирамиды.
Прямоугольный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
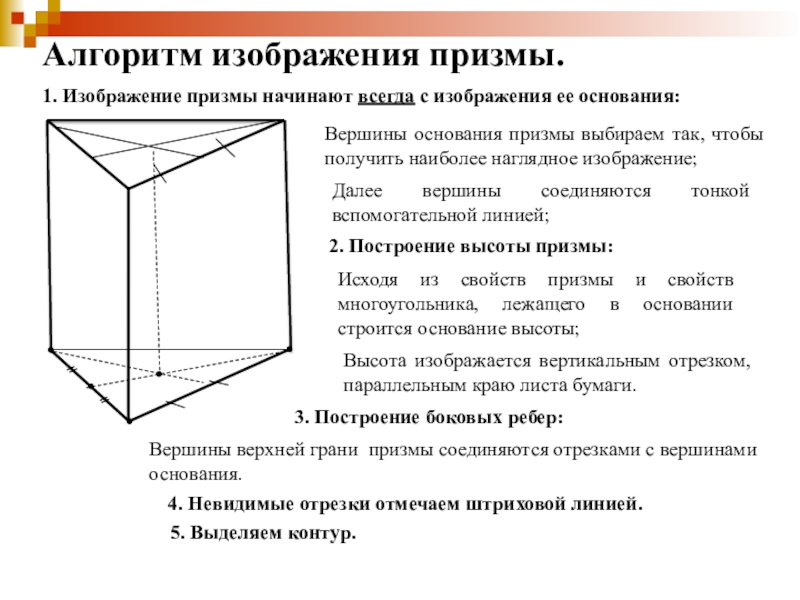
Слайд 233. Построение боковых ребер:
Вершины верхней грани призмы соединяются отрезками с вершинами
4. Невидимые отрезки отмечаем штриховой линией.
5. Выделяем контур.
Алгоритм изображения призмы.
1. Изображение призмы начинают всегда с изображения ее основания:
Вершины основания призмы выбираем так, чтобы получить наиболее наглядное изображение;
Далее вершины соединяются тонкой вспомогательной линией;
2. Построение высоты призмы:
Исходя из свойств призмы и свойств многоугольника, лежащего в основании строится основание высоты;
Высота изображается вертикальным отрезком, параллельным краю листа бумаги.
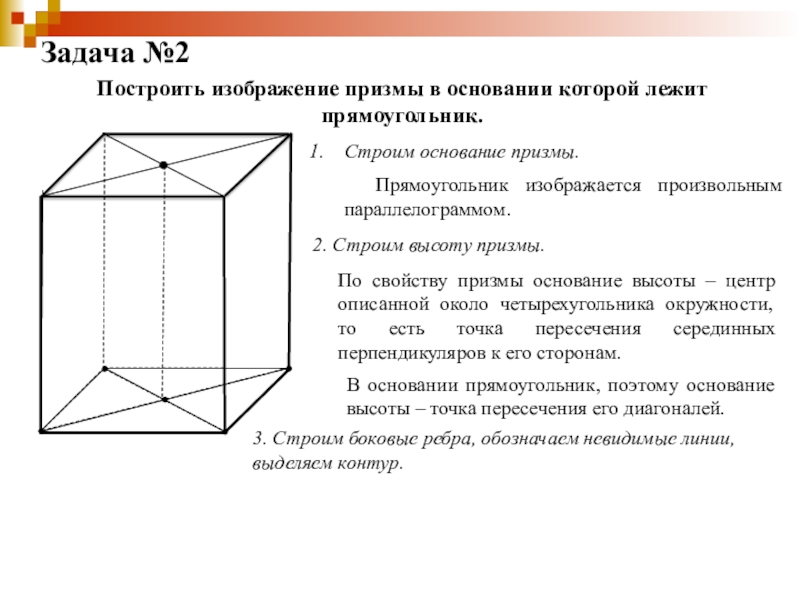
Слайд 24Задача №2
Построить изображение призмы в основании которой лежит прямоугольник.
Строим основание призмы.
Прямоугольник изображается произвольным параллелограммом.
2. Строим высоту призмы.
По свойству призмы основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольник, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.