Сабақтың міндеттері:
Квадрат функцияның қасиеттерін қайталау.
Кавдрат теңсіздікті графиктік тәсілмен шешу дағдысын үйрену.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Ашық сабақ Квадрат теңсіздіктерді шешу
Содержание
1) у = -х²-3х-3 2) у = х²+4х-5 3) у = х² -2х+14) у = х²+5х+ 7 5) у = - х² +2х-1 6) у = - х²+4х+5А В
Слайд 1Тақырыбы: Квадрат теңсіздік.Квадрат теңсіздікті квадрат функцияның графигі арқылы шешу
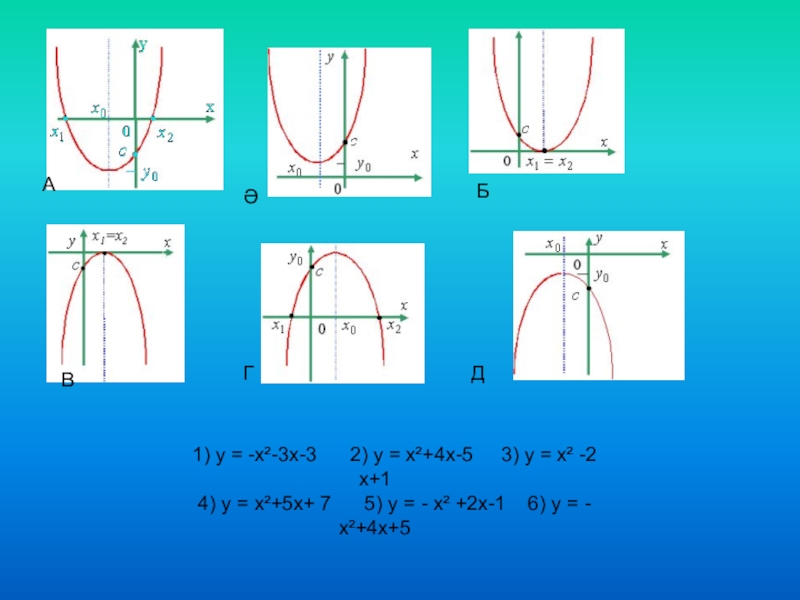
Слайд 21) у = -х²-3х-3 2) у = х²+4х-5
3) у = х² -2х+1
4) у = х²+5х+ 7 5) у = - х² +2х-1 6) у = - х²+4х+5
4) у = х²+5х+ 7 5) у = - х² +2х-1 6) у = - х²+4х+5
А
В
Ә
Б
Г
Д
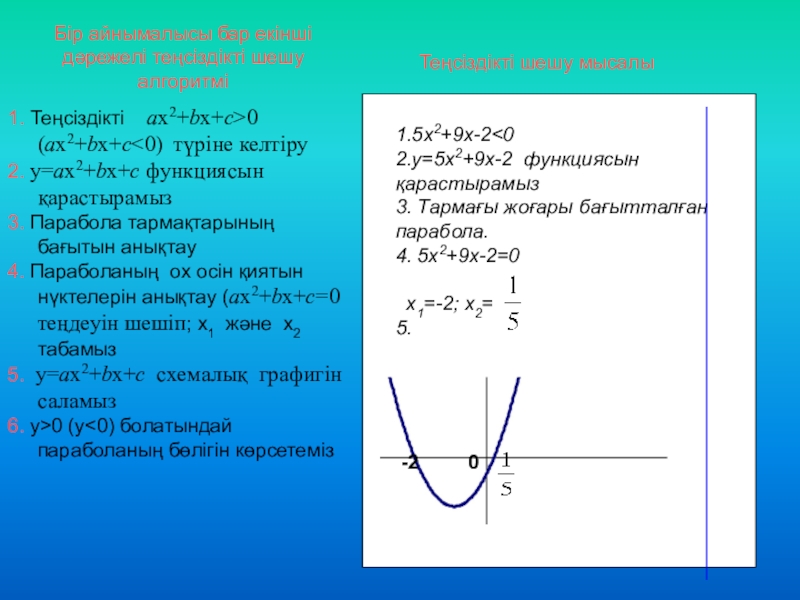
Слайд 3Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі
1.5х2+9х-2
жоғары бағытталған парабола.
4. 5х2+9х-2=0
х1=-2; х2=
5.
4. 5х2+9х-2=0
х1=-2; х2=
5.
-2
0
1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c<0) түріне келтіру
2. y=ax2+bx+c функциясын қарастырамыз
3. Парабола тармақтарының бағытын анықтау
4. Параболаның ох осін қиятын нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз
5. y=ax2+bx+c схемалық графигін саламыз
6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз
Теңсіздікті шешу мысалы
Слайд 4
-2
0
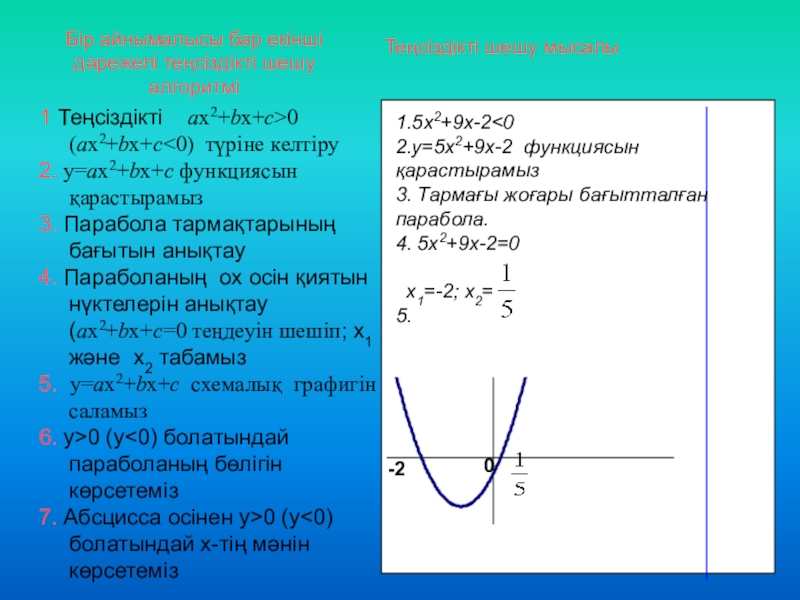
1 Теңсіздікті ax2+bx+c>0 (ax2+bx+c
тармақтарының бағытын анықтау
4. Параболаның ох осін қиятын нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз
5. y=ax2+bx+c схемалық графигін саламыз
6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз
4. Параболаның ох осін қиятын нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз
5. y=ax2+bx+c схемалық графигін саламыз
6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз
Теңсіздікті шешу мысалы
Бір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі
1.5х2+9х-2<0
2.y=5х2+9х-2 функциясын қарастырамыз
3. Тармағы жоғары бағытталған парабола.
4. 5х2+9х-2=0
х1=-2; х2=
5.
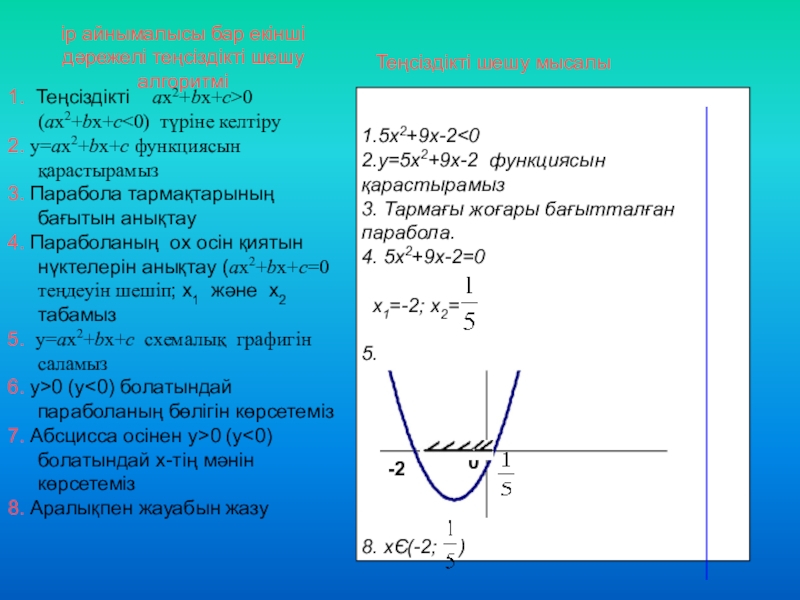
Слайд 5ір айнымалысы бар екінші дәрежелі теңсіздікті шешу алгоритмі
1.5х2+9х-2
жоғары бағытталған парабола.
4. 5х2+9х-2=0
х1=-2; х2=
5.
8. хЄ(-2; )
4. 5х2+9х-2=0
х1=-2; х2=
5.
8. хЄ(-2; )
-2
0
1. Теңсіздікті ax2+bx+c>0 (ax2+bx+c<0) түріне келтіру
2. y=ax2+bx+c функциясын қарастырамыз
3. Парабола тармақтарының бағытын анықтау
4. Параболаның ох осін қиятын нүктелерін анықтау (ax2+bx+c=0 теңдеуін шешіп; х1 және х2 табамыз
5. y=ax2+bx+c схемалық графигін саламыз
6. y>0 (y<0) болатындай параболаның бөлігін көрсетеміз
7. Абсцисса осінен y>0 (y<0) болатындай х-тің мәнін көрсетеміз
8. Аралықпен жауабын жазу
Теңсіздікті шешу мысалы
