Потоцким Павлом и Дворянкиным Михаилом под руководством учителя математики 159 гимназии Ширяевой Надежды Борисовны
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект, выполненный учениками 9 класса для подготовки к ГИА по математие под руководством учителя
Содержание
- 1. Проект, выполненный учениками 9 класса для подготовки к ГИА по математие под руководством учителя
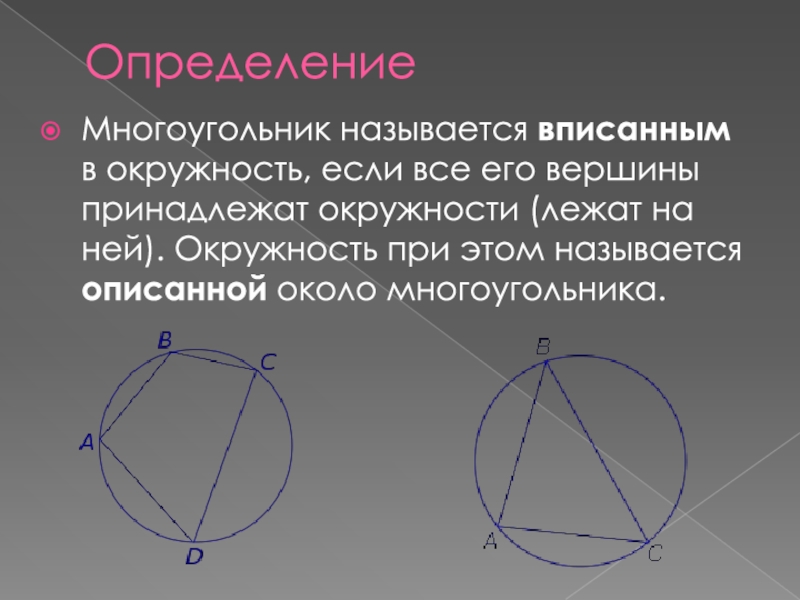
- 2. ОпределениеМногоугольник называется вписанным в окружность, если все
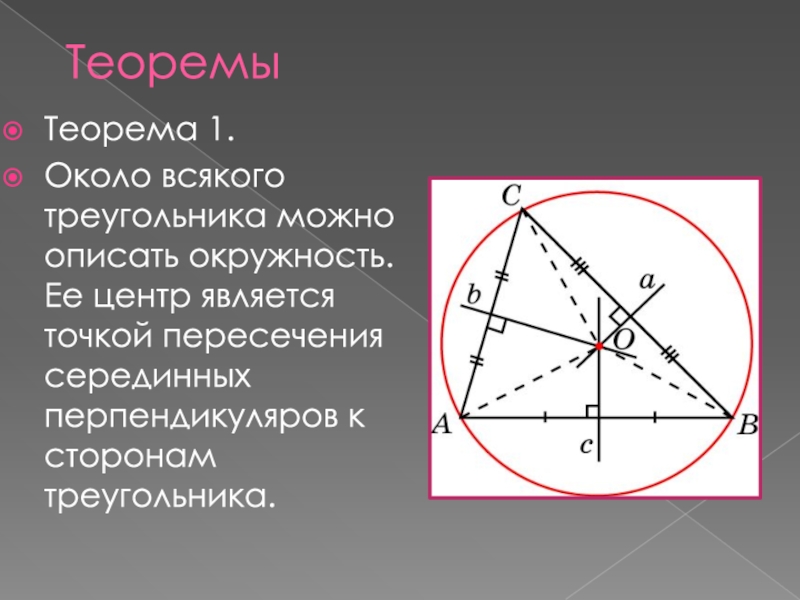
- 3. ТеоремыТеорема 1.Около всякого треугольника можно описать окружность.
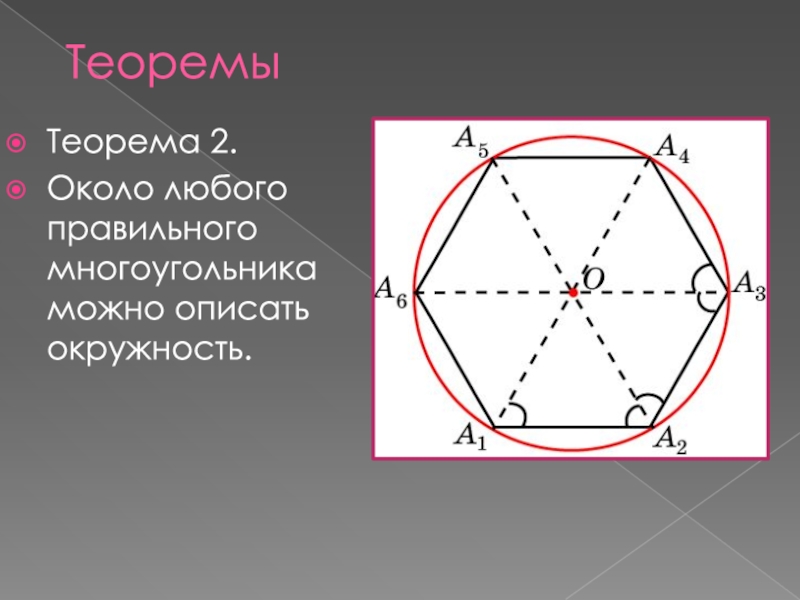
- 4. ТеоремыТеорема 2.Около любого правильного многоугольника можно описать окружность.
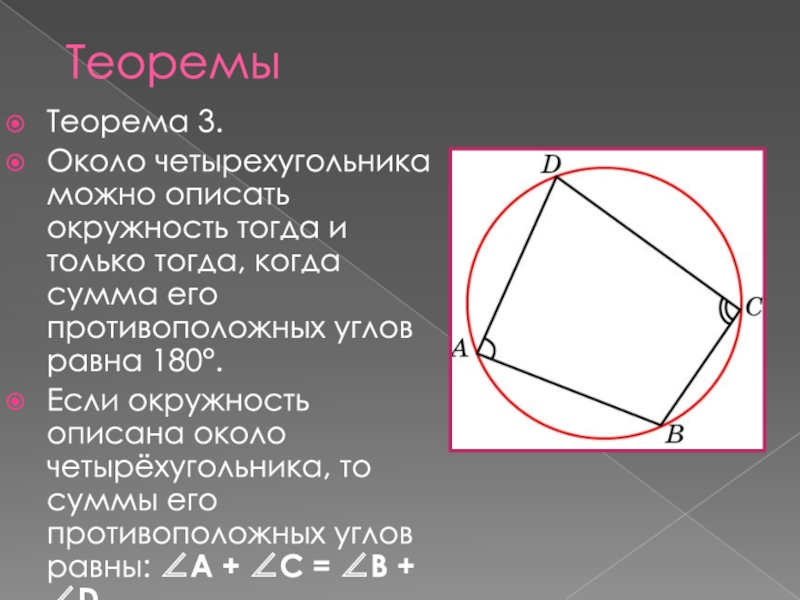
- 5. Теорема 3.Около четырехугольника можно описать окружность тогда
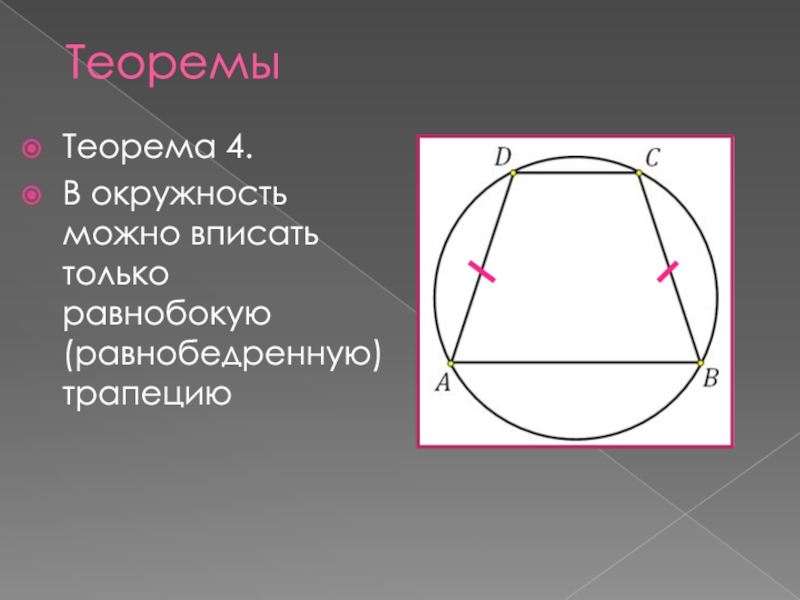
- 6. Теорема 4.В окружность можно вписать только равнобокую (равнобедренную) трапециюТеоремы
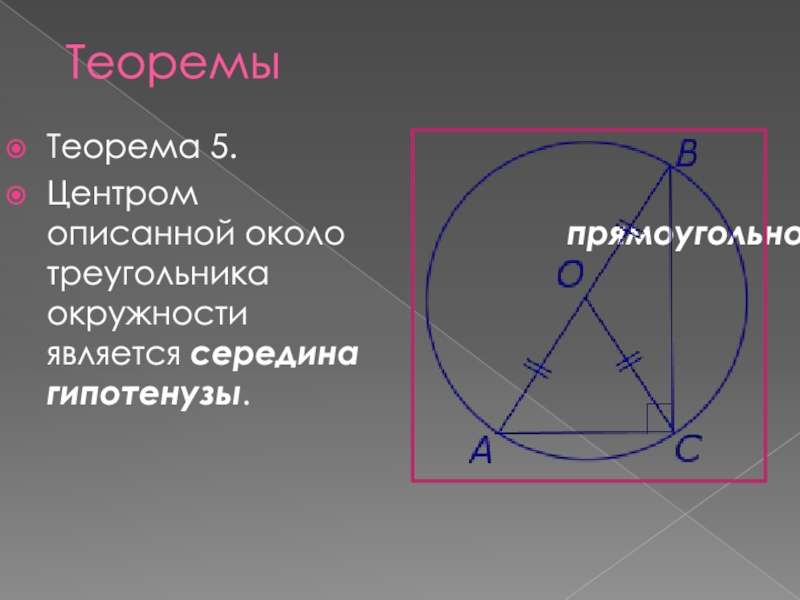
- 7. Теорема 5.Центром описанной около
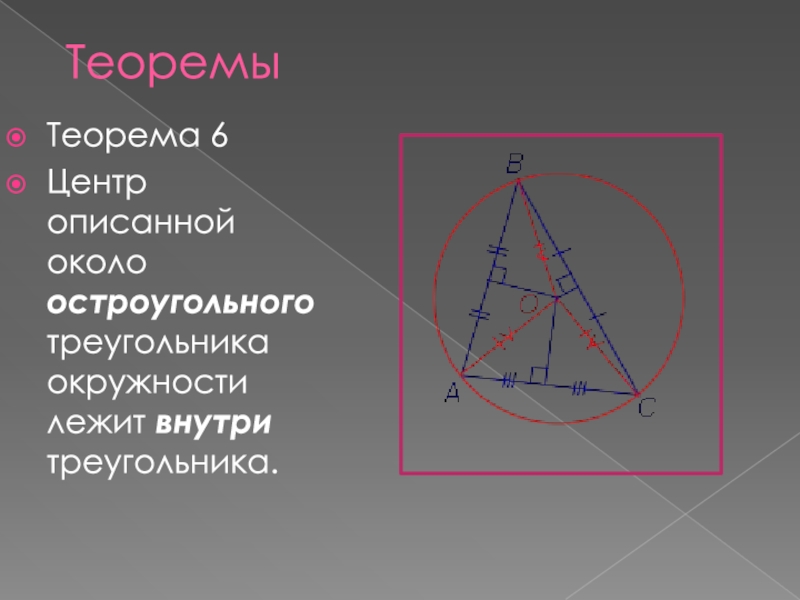
- 8. Теорема 6Центр описанной около
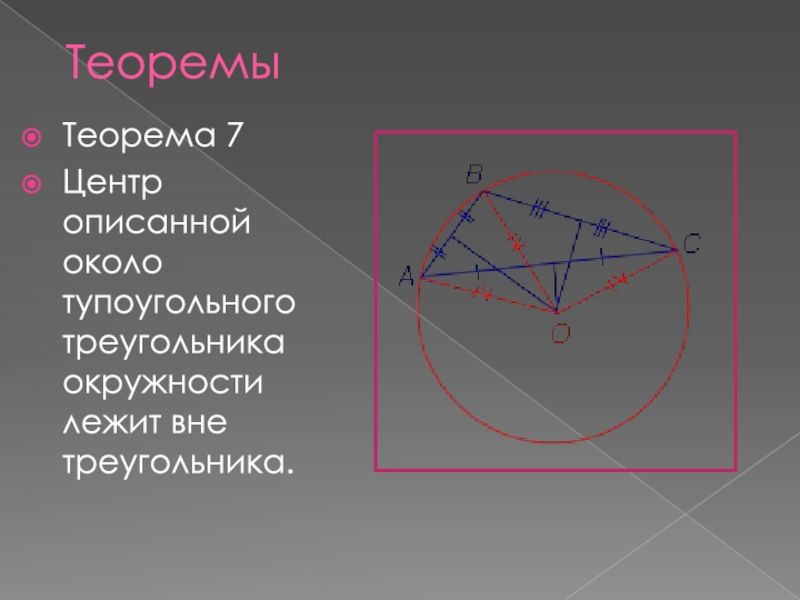
- 9. Теорема 7Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.Теоремы
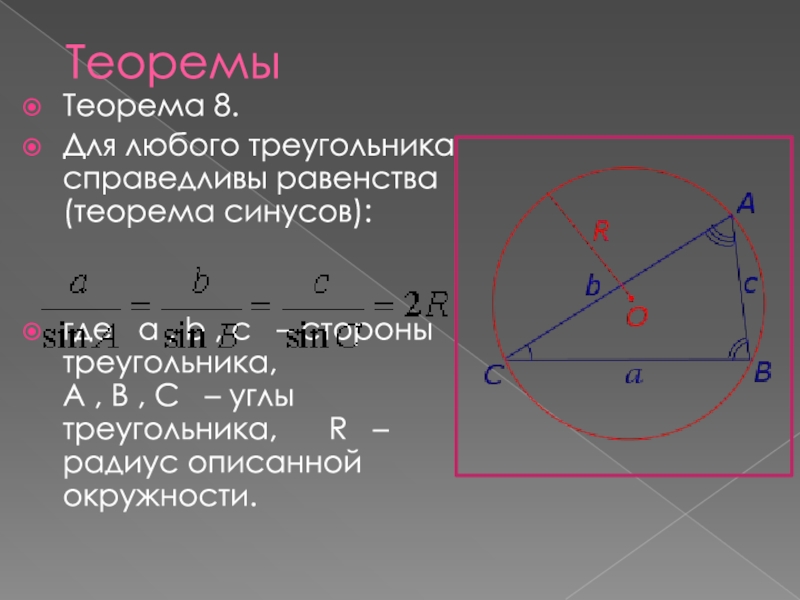
- 10. Теорема 8.Для любого треугольника справедливы равенства (теорема
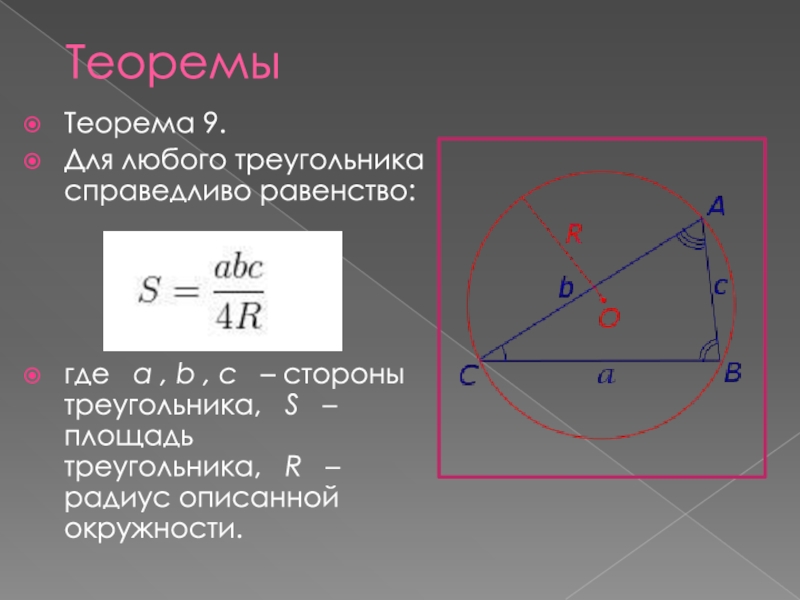
- 11. Теорема 9.Для любого треугольника справедливо равенство:где a
- 12. Задача 1.Нахождение величины угла правильного шестиугольника.В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.Задачи
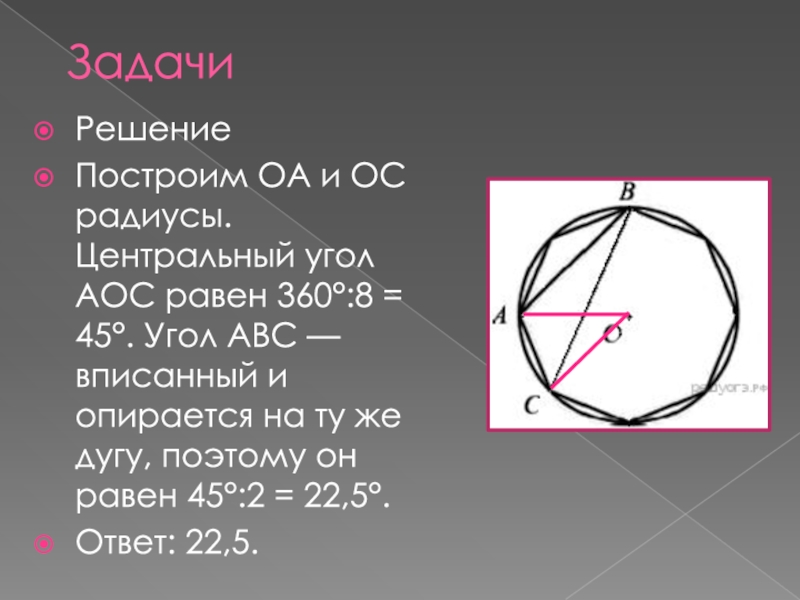
- 13. РешениеПостроим OA и OC радиусы. Центральный угол
- 14. Задача 2.Нахождение величины угла правильной фигуры от
- 15. РешениеУгол ABC — вписанный и опирается на диаметр AC. Таким образом, угол ABC = 90°.Ответ: 90.Задачи
- 16. Задача 3.Нахождение диаметра описанной окружности.Боковая сторона равнобедренного
- 17. РешениеВоспользуемся теоремой косинусов:Здесь a и b — боковые стороны равнобедренного треугольника, c — основание.Диаметр описанной окружности вычислим по формуле:ЗадачиОтвет:8
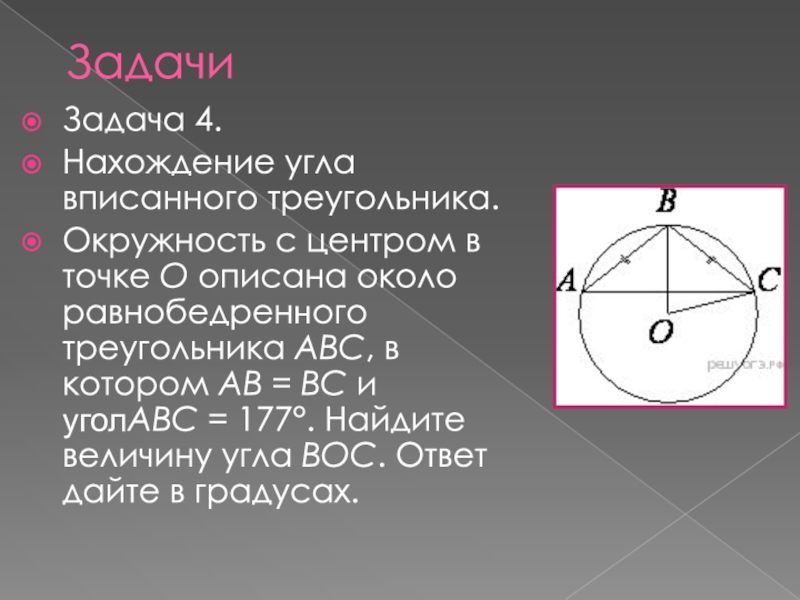
- 18. Задача 4.Нахождение угла вписанного треугольника.Окружность с центром
- 19. РешениеСумма углов треугольника равна 180°. Треугольник — равнобедренный,
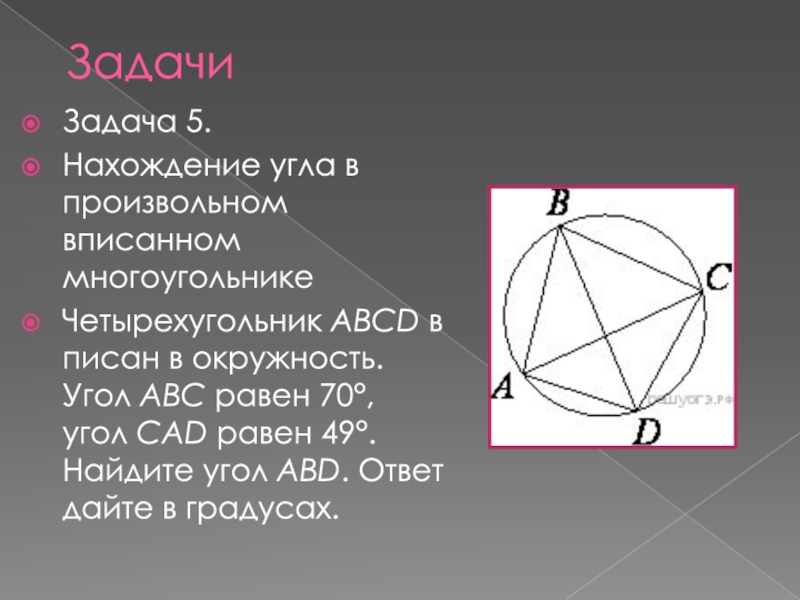
- 20. Задача 5.Нахождение угла в произвольном вписанном многоугольникеЧетырехугольник ABCD вписан
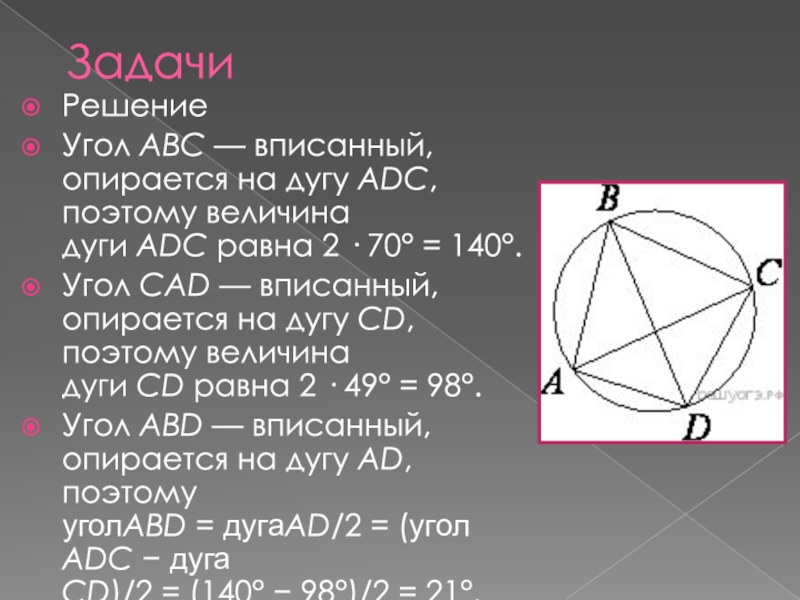
- 21. РешениеУгол ABC — вписанный, опирается на дугу ADC, поэтому величина
- 22. Задача 6.Нахождение площади квадрата.Найдите площадь квадрата, описанного вокруг окружности радиуса 7.Задачи
- 23. РешениеПусть R и D соответственно радиус и диаметр окружности, a — сторона
- 24. СПАСИБО ЗА ВНИМАНИЕ!
ОпределениеМногоугольник называется вписанным в окружность, если все его вершины принадлежат окружности (лежат на ней). Окружность при этом называется описанной около многоугольника.
Слайд 2Определение
Многоугольник называется вписанным в окружность, если все его вершины принадлежат окружности
(лежат на ней). Окружность при этом называется описанной около многоугольника.
Слайд 3Теоремы
Теорема 1.
Около всякого треугольника можно описать окружность. Ее центр является точкой
пересечения серединных перпендикуляров к сторонам треугольника.
Слайд 5Теорема 3.
Около четырехугольника можно описать окружность тогда и только тогда, когда
сумма его противоположных углов равна 180°.
Если окружность описана около четырёхугольника, то суммы его противоположных углов равны: A + C = B + D
Если окружность описана около четырёхугольника, то суммы его противоположных углов равны: A + C = B + D
Теоремы
Слайд 7Теорема 5.
Центром описанной около
прямоугольного треугольника окружности является середина гипотенузы.
Теоремы
Слайд 8Теорема 6
Центр описанной около
остроугольного треугольника окружности лежит внутри треугольника.
Теоремы
Слайд 9Теорема 7
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теоремы
Слайд 10Теорема 8.
Для любого треугольника справедливы равенства (теорема синусов):
где a ,
b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Теоремы
Слайд 11Теорема 9.
Для любого треугольника справедливо равенство:
где a , b , c
– стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Теоремы
Слайд 12Задача 1.
Нахождение величины угла правильного шестиугольника.
В окружность вписан равносторонний восьмиугольник. Найдите
величину угла ABC.
Задачи
Слайд 13Решение
Построим OA и OC радиусы. Центральный угол AOC равен 360°:8 =
45°. Угол ABC — вписанный и опирается на ту же дугу, поэтому он равен 45°:2 = 22,5°.
Ответ: 22,5.
Ответ: 22,5.
Задачи
Слайд 14Задача 2.
Нахождение величины угла правильной фигуры от 6-ти углов и более.
В
окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
Задачи
Слайд 15Решение
Угол ABC — вписанный и опирается на диаметр AC. Таким образом, угол ABC = 90°.
Ответ: 90.
Задачи
Слайд 16Задача 3.
Нахождение диаметра описанной окружности.
Боковая сторона равнобедренного треугольника равна 4. Угол
при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Задачи
Слайд 17Решение
Воспользуемся теоремой косинусов:
Здесь a и b — боковые стороны равнобедренного треугольника, c — основание.
Диаметр описанной
окружности вычислим по формуле:
Задачи
Ответ:8
Слайд 18Задача 4.
Нахождение угла вписанного треугольника.
Окружность с центром в точке O описана около равнобедренного
треугольника ABC, в котором AB = BC и уголABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.
Задачи
Слайд 19Решение
Сумма углов треугольника равна 180°. Треугольник — равнобедренный, следовательно,
Угол BAC — вписанный, поэтому
он равен половине дуги, на которую опирается. Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается. Углы BAC и BOC опираются на одну и ту же дугу, следовательно,
Задачи
Ответ: 3.
Слайд 20Задача 5.
Нахождение угла в произвольном вписанном многоугольнике
Четырехугольник ABCD вписан в окружность. Угол ABC равен 70°,
угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Задачи
Слайд 21Решение
Угол ABC — вписанный, опирается на дугу ADC, поэтому величина дуги ADC равна 2 · 70° = 140°.
Угол CAD — вписанный,
опирается на дугу CD, поэтому величина дуги CD равна 2 · 49° = 98°.
Угол ABD — вписанный, опирается на дугу AD, поэтому уголABD = дугаAD/2 = (угол ADC − дуга CD)/2 = (140° − 98°)/2 = 21°.
Ответ: 21.
Угол ABD — вписанный, опирается на дугу AD, поэтому уголABD = дугаAD/2 = (угол ADC − дуга CD)/2 = (140° − 98°)/2 = 21°.
Ответ: 21.
Задачи
Слайд 22Задача 6.
Нахождение площади квадрата.
Найдите площадь квадрата, описанного вокруг окружности радиуса 7.
Задачи
Слайд 23Решение
Пусть R и D соответственно радиус и диаметр окружности, a — сторона квадрата. Сторона квадрата равна
диаметру вписанной окружности. Найдём площадь квадрата:
Задачи
Ответ: 196.
