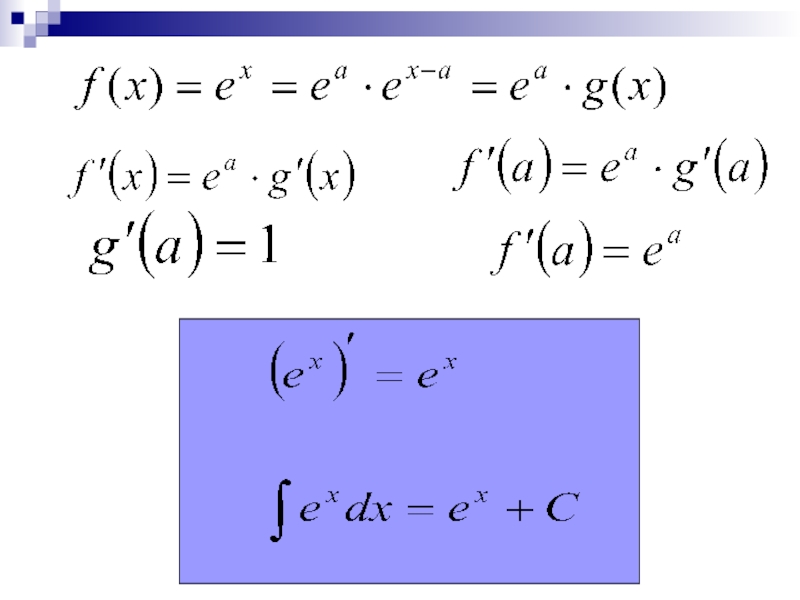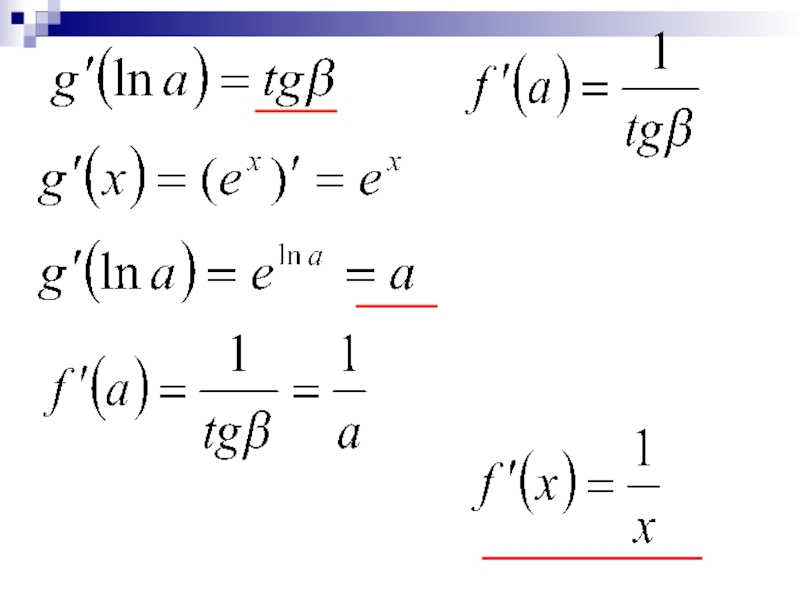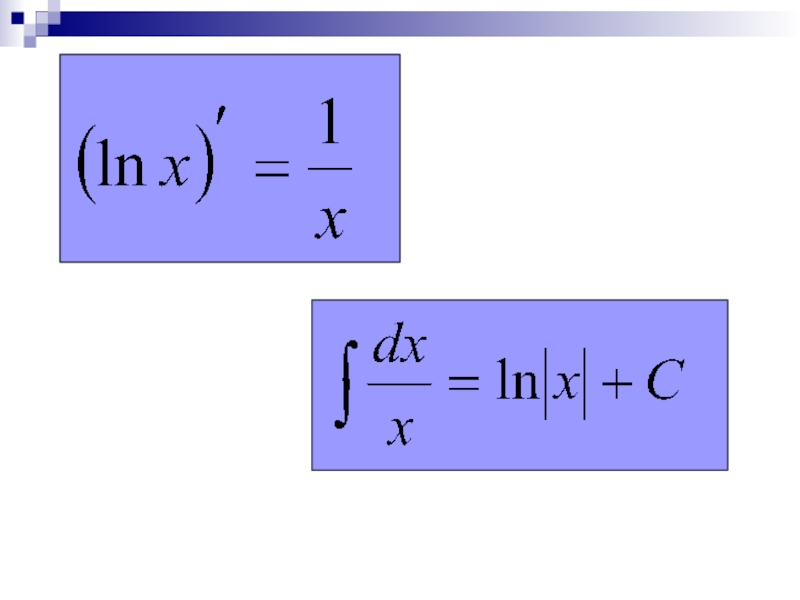- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Дифференцирование показательной и логарифмической функции
Содержание
- 1. Дифференцирование показательной и логарифмической функции
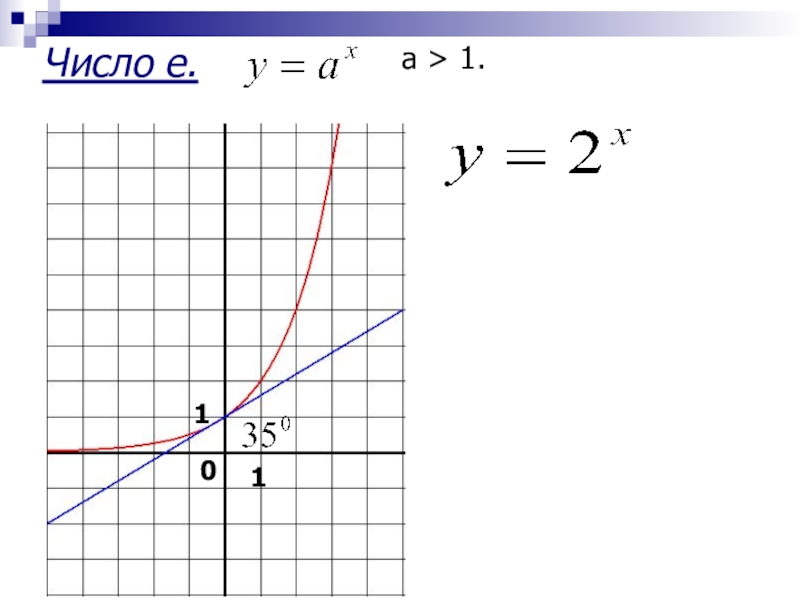
- 2. Число e. а > 1. 110
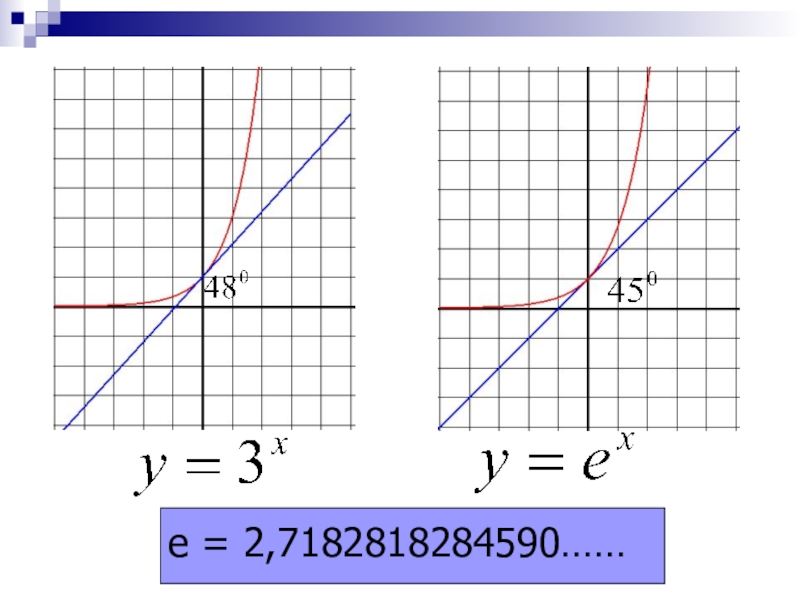
- 3. e = 2,7182818284590……
- 4. Свойства функции :1. не является четной ,
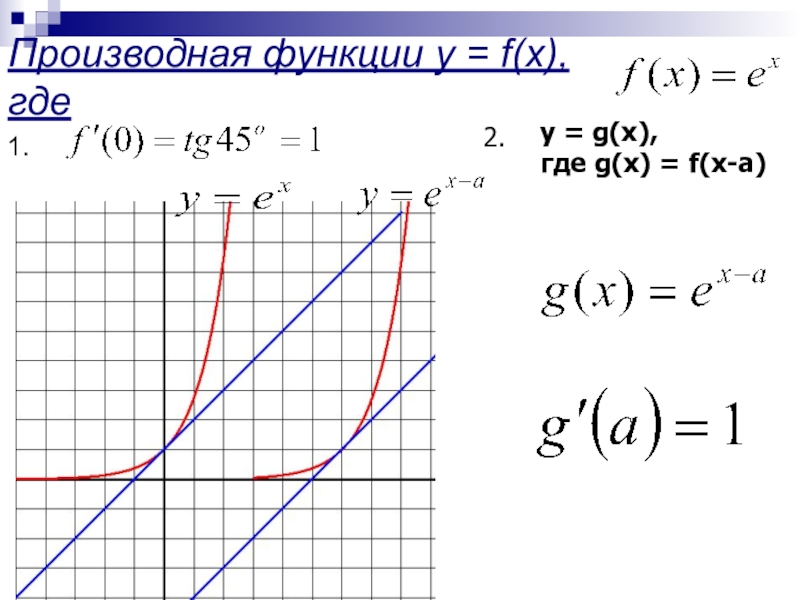
- 5. Производная функции y = f(x), где y
- 6. Слайд 6
- 7. Пример 1. Провести касательную к графику функции
- 8. Пример 2.Вычислить значение производной функции
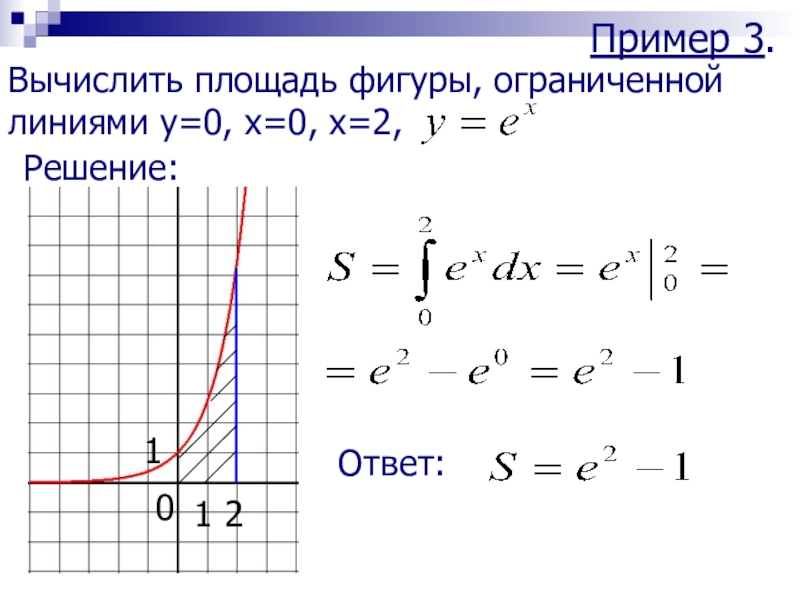
- 9. Пример 3.Вычислить площадь фигуры, ограниченной линиями y=0, x=0, x=2, Решение:2110Ответ:
- 10. Пример 4.Исследовать на экстремум и схематически изобразить график функцииРешение:1)2)
- 11. 3)-2x0++-4)x=-2 – точка максимумаx=0 – точка минимума
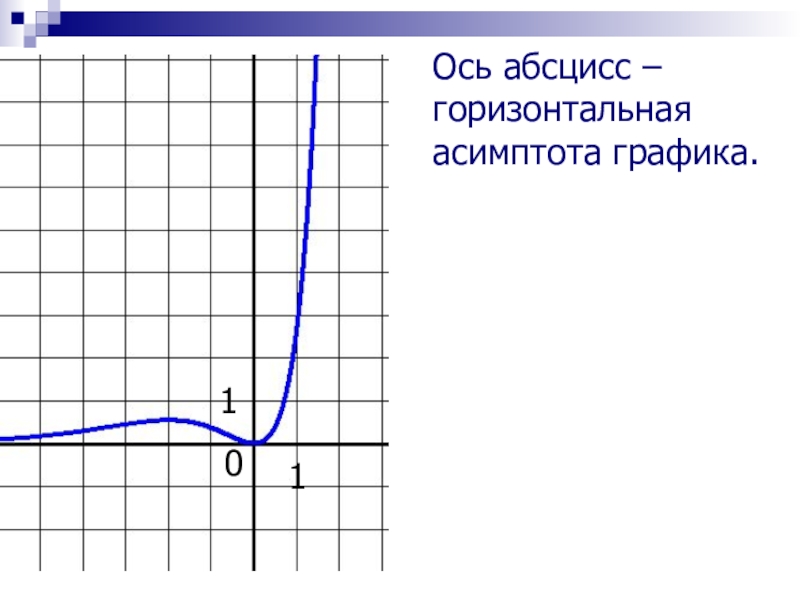
- 12. Ось абсцисс – горизонтальная асимптота графика.011
- 13. Решите упражнения:1620, 1623(a,б), 1624(а,б), 1628(а,б), 1629(а,б)Решить дома: 1621, 1623(в,г), 1624(в,г), 1628(в,г), 1629(в,г), 1631.
- 14. Натуральные логарифмы:
- 15. 1. не является четной ,
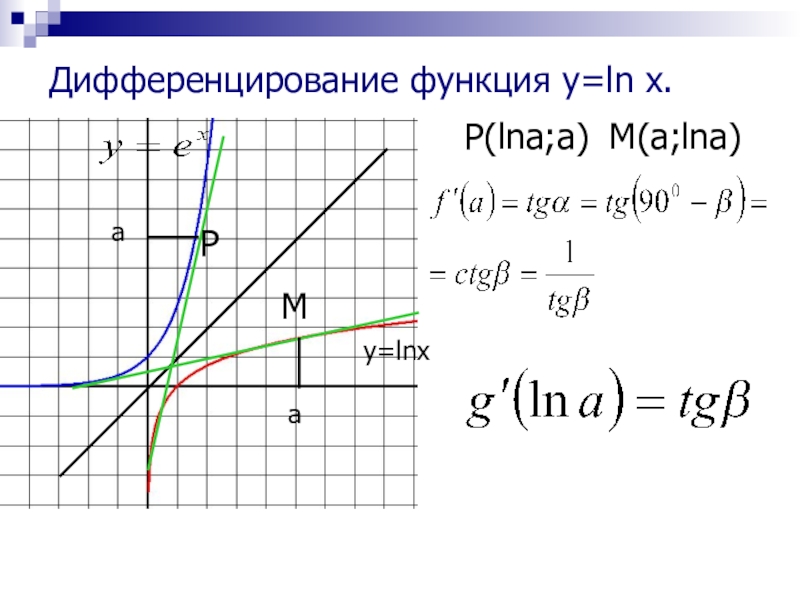
- 16. Дифференцирование функция y=ln x. y=lnxaaP(lna;a)PMM(a;lna)
- 17. Слайд 17
- 18. Слайд 18
- 19. Дифференцирование функции Например,
- 20. Дифференцирование функции
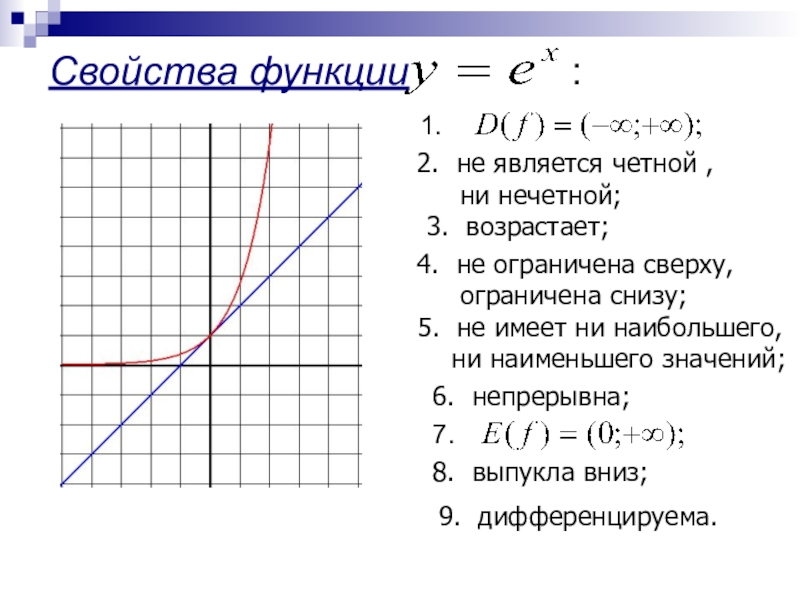
Слайд 4Свойства функции
:
1.
не является четной ,
ни нечетной;
3.
не ограничена сверху,
ограничена снизу;
не имеет ни наибольшего,
ни наименьшего значений;
6. непрерывна;
7.
8. выпукла вниз;
9. дифференцируема.
Слайд 7Пример 1. Провести касательную к графику функции
Решение:
1) a=1
2) f(a)=f(1)=e
3)
4) y=e+e(x-1); y = ex
Ответ:
y=ex
Слайд 13Решите упражнения:
1620, 1623(a,б), 1624(а,б), 1628(а,б), 1629(а,б)
Решить дома: 1621, 1623(в,г), 1624(в,г), 1628(в,г),
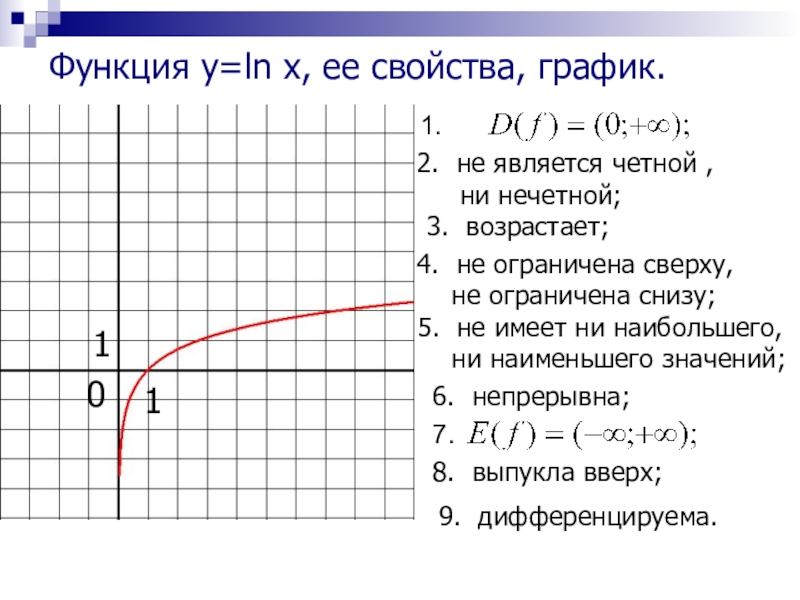
Слайд 151.
не является четной ,
ни нечетной;
3. возрастает;
не
не ограничена снизу;
не имеет ни наибольшего,
ни наименьшего значений;
6. непрерывна;
7.
8. выпукла вверх;
9. дифференцируема.
Функция y=ln x, ее свойства, график.
0
1
1