ShareSlide^ru

Презентация, доклад на тему Открытый урок по алгебре в 10 классе Применение производной

Содержание

1. Открытый урок по алгебре в 10 классе Применение производной
2. Цели и задачи: 1.2.3.
3. Признаки возрастания и убывания функции
4. Если f’(x) > 0 в каждой точке
5. Слайд 5
6. Критические точки Экстремумы функции
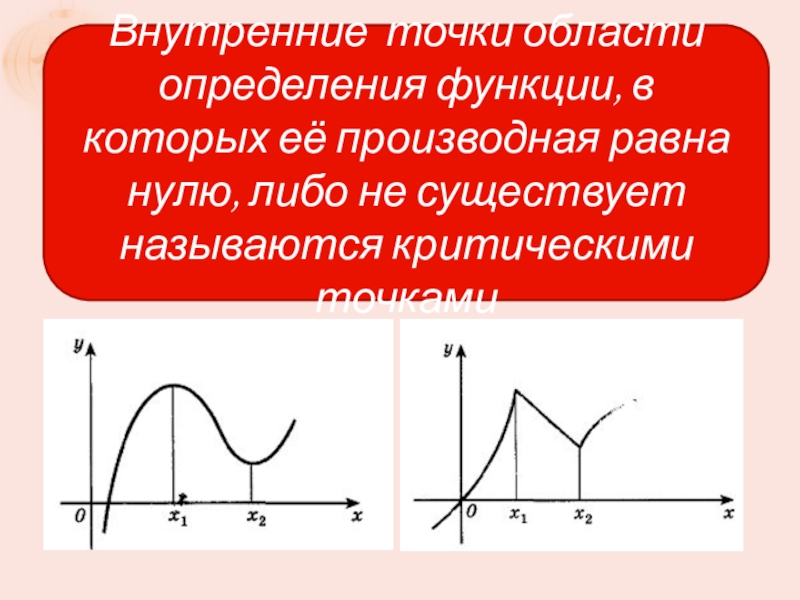
7. Внутренние точки области определения функции, в которых
8. Пьер ФермаЕсли точка xo является точкой экстремума
9. Признак максимума функцииЕсли функция f непрерывна в
10. Признак минимума функцииЕсли функция f непрерывна в
11. Находим f ‘(x)Определяем критические точки функции f(x),
12. Находим максимум и минимумНаходим экстремальные значения функции
13. Слайд 13
14. Слайд 14
15. ДОМАШНЕЕ ЗАДАНИЕПовторить основные алгоритмы и понятия

Цели и задачи: 1.2.3.

Главная
Алгебра
Открытый урок по алгебре в 10 классе Применение производной

Слайд 1Обобщающий урок по теме «Применение производной к исследованию функций»

Обобщающий урок по теме «Применение производной к исследованию функций»

Слайд 2Цели и задачи:
1.
2.
3.

Цели и задачи: 1.2.3.

Слайд 3Признаки возрастания и убывания функции

Признаки возрастания и убывания функции

Слайд 4Если f’(x) > 0 в каждой точке интервала I, то функция

f возрастает на I

Если f’(x) < 0 в каждой точке интервала I, то функция f убывает на I

Если f’(x) > 0 в каждой точке интервала I, то функция f возрастает на IЕсли f’(x) <

Слайд 5

Слайд 6Критические точки Экстремумы функции

Критические точки Экстремумы функции

Слайд 7Внутренние точки области определения функции, в которых её производная равна нулю,

либо не существует называются критическими точками

Внутренние точки области определения функции, в которых её производная равна нулю, либо не существует называются критическими точками

Слайд 8Пьер Ферма
Если точка xo является точкой экстремума функции f и в

этой точке существует её производная f’, то:
f’(x0) = 0

Необходимое условие
экстремума

Пьер ФермаЕсли точка xo является точкой экстремума функции f и в этой точке существует её производная f’,

Слайд 9Признак максимума функции
Если функция f непрерывна в точке x0, а f’(x0)

> 0 на интервале (a ; x0), и f’(x0) < 0 на интервале (x0 ; b) , то точка x0 является точкой максимума

Если в точке x0 функция меняет знак с «+» на «-», то точка x0 является точкой максимума

Признак максимума функцииЕсли функция f непрерывна в точке x0, а f’(x0) > 0 на интервале (a ;

Слайд 10Признак минимума функции
Если функция f непрерывна в точке x0, а f’(x0)

< 0 на интервале (a ; x0), и f’(x0) > 0 на интервале (x0 ; b) , то точка x0 является точкой минимума

Если в точке x0 функция меняет знак с «-» на «+», то точка x0 является точкой минимума

Признак минимума функцииЕсли функция f непрерывна в точке x0, а f’(x0) < 0 на интервале (a ;

Слайд 11Находим f ‘(x)
Определяем критические точки функции f(x), т.е. точки, в которых

f ‘(x)=0 . Располагаем их в порядке возрастания.
Определяем знак f ‘(х) на каждом из промежутков (а;в) в критических точках

Алгоритм нахождения экстремумов функции

Находим f ‘(x)Определяем критические точки функции f(x), т.е. точки, в которых f ‘(x)=0 . Располагаем их в

Слайд 12Находим максимум и минимум
Находим экстремальные значения функции в точках максимум и

минимум
Если не указан интервал, на котором исследуется функция у=f(х) на экстремум, то вначале следует найти область ее определения.

Алгоритм нахождения экстремумов функции

Находим максимум и минимумНаходим экстремальные значения функции в точках максимум и минимумЕсли не указан интервал, на котором

Слайд 13

Слайд 14

Слайд 15ДОМАШНЕЕ ЗАДАНИЕ
Повторить основные алгоритмы и понятия

ДОМАШНЕЕ ЗАДАНИЕПовторить основные алгоритмы и понятия

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть