нүктелері
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Функцияның өусу, кему аралығы
Содержание
- 1. Презентация Функцияның өусу, кему аралығы
- 2. Слайд 2
- 3. α xy
- 4. Егер дифференциалданатын f(x) функцияcының туындысы Х аралығының
- 5. y= f(x)
- 6. Егер дифференциалданатын f(x) функцияcының туындысы Х аралығының
- 7. Дәлелдеу: Х аралығына жататын х1 және х2
- 8. Сонғы теңдеудің оң бөлігі де оң мәнді
- 9. 2.ТЕОРЕМА (функция кему үшін жеткілікті шарттар) Егер
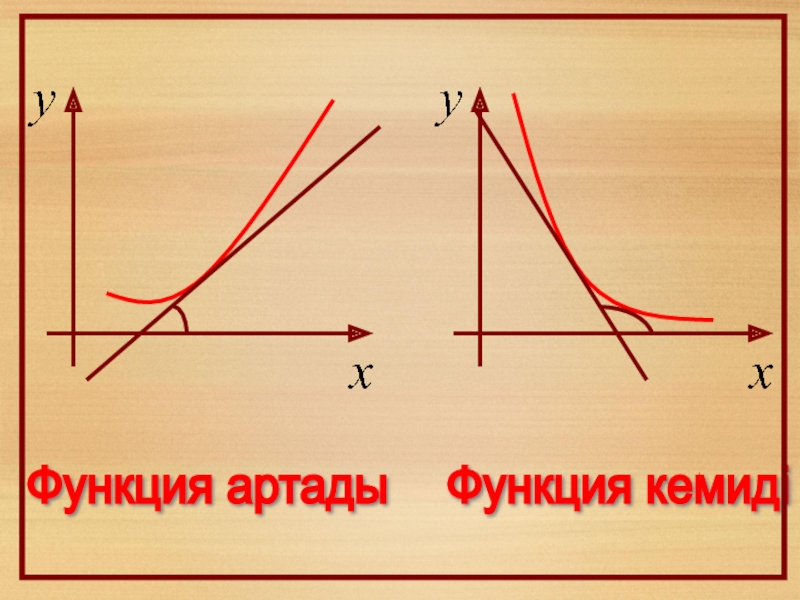
- 10. Функция артады Функция кемиді
- 11. Мысал. Функцияның біркелкі аралығын табу
- 12. Шешімі: Бұл функцияның туындысын табамыз: Бұл туындының
Білім деген биік шың, Бақытқа сені жеткізер, Білім деген ақылшың Қиындықтан өткізер
Слайд 4Егер дифференциалданатын f(x)
функцияcының туындысы Х
аралығының әрбір нүктесінде оң
таңбалы
болса, функция осы аралықта
өспелі болады .
өспелі болады .
Слайд 6Егер дифференциалданатын f(x)
функцияcының туындысы Х
аралығының әрбір нүктесінде теріс
таңбалы болса,
функция осы аралықта
кемімелі болады .
кемімелі болады .
Слайд 7Дәлелдеу:
Х аралығына жататын х1 және х2 мәндерін қарастырайық.
Егер
[x1;x2] аралығында f(x)
функциясы үшін Лагранж теоремасы жүзеге асады
Егер
Сонда, ξ функцияның туындысы он мәніндегі аралыққа жатады
![Дәлелдеу: Х аралығына жататын х1 және х2 мәндерін қарастырайық.Егер[x1;x2] аралығында f(x) функциясы үшін Лагранж теоремасы жүзеге асадыЕгерСонда,](/img/thumbs/f2e41e8fde7be594b5addecc73d8af7b-800x.jpg "Презентация Функцияның өусу, кему аралығы Дәлелдеу: Х аралығына жататын х1 және х2 мәндерін қарастырайық.Егер[x1;x2] аралығында f(x)")
Слайд 8Сонғы теңдеудің оң бөлігі де оң мәнді болады
Сонда сол жақ болігі
де он мәнді болды :
яғни
Сонда біз аргументтің көп мәніне функцияның көп мәні сәйкес келетінің дәлелдедік. Бұл функция артып келеді дегенді білдіреді.
Слайд 92.ТЕОРЕМА (функция кему үшін жеткілікті шарттар)
Егер сараланатын функциялардың
туындысы кейбір
х аралықтарында
теріс болса, функция осы аралықта
кемиді .
теріс болса, функция осы аралықта
кемиді .
Слайд 12Шешімі:
Бұл функцияның туындысын табамыз:
Бұл туындының белгісін анықтацмыз :
Функция
аралығында артады
Функция аралығында кемиді
