задание № 5
Учитель математики Юрьева О.А.
МБОУ «СОШ №6»,
г. Нефтеюганск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Растяжения и сдвиги графиков функций 9 класс
Содержание
- 1. Презентация по математике на тему Растяжения и сдвиги графиков функций 9 класс
- 2. Слайд 2
- 3. Слайд 3
- 4. 2) На одном из рисунков изображена гипербола. Укажите номер этого рисунка. 2
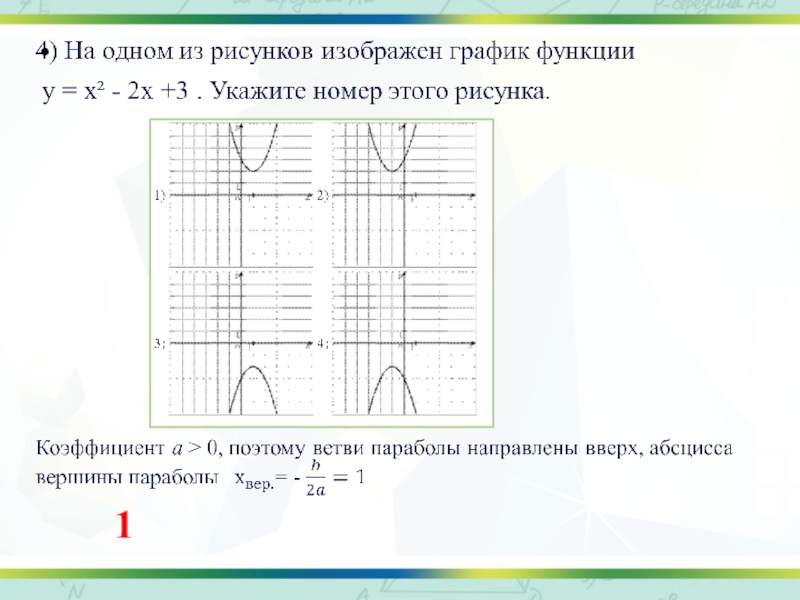
- 5. 3) График какой из приведенных ниже функций
- 6. 1
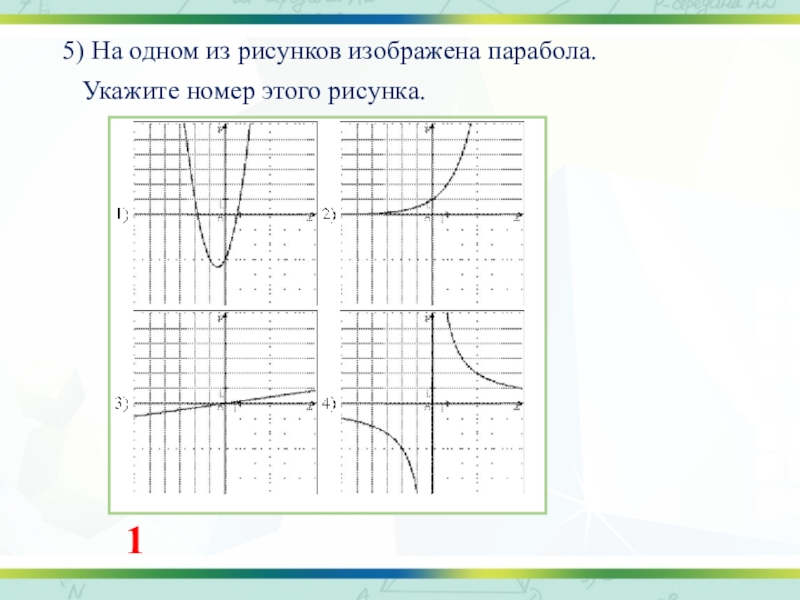
- 7. 5) На одном из рисунков изображена парабола. Укажите номер этого рисунка.1
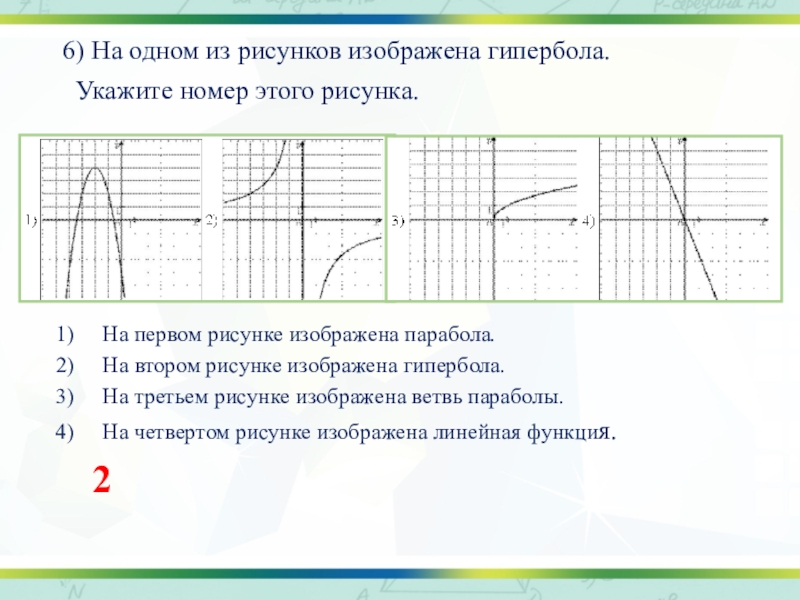
- 8. 6) На одном из рисунков изображена гипербола.
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
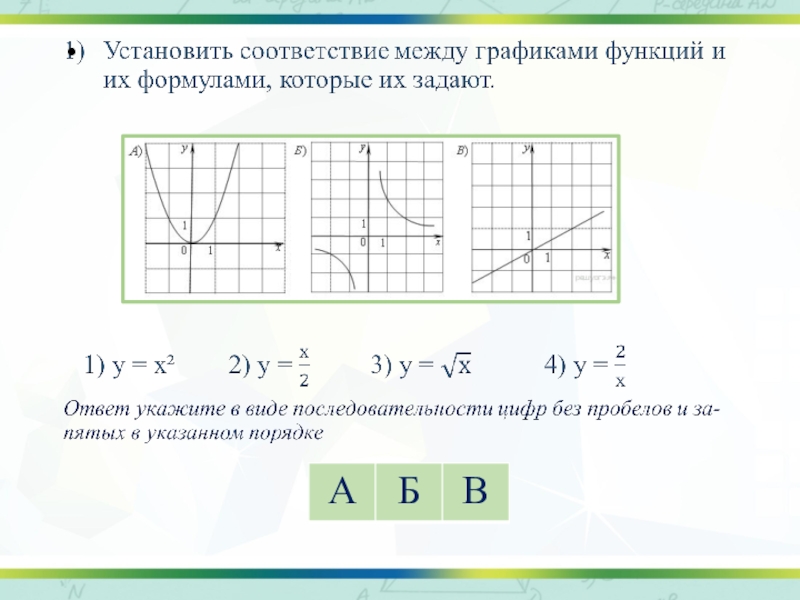
- 12. 9) Установите соответствие между функциями и их
- 13. Слайд 13
- 14. А) у = х² - 2х ветви
- 15. 10) На рисунке изображены графики функций вида
- 16. График функции у = aх² +
- 17. 11) Установите соответствие между графиками функций и
- 18. Все изображённые здесь графики - прямые. Уравнение
- 19. 11) Установите соответствие между функциями и их
- 20. Если прямая задана уравнением у =
- 21. Слайд 21
- 22. Слайд 22
- 23. 13) На рисунке изображены графики функций вида
- 24. ГрафикиКоэффициенты1) k < 0, b > 0
- 25. 14) Установите соответствие между функциями и их
- 26. Источник содержания:Сайт «Решу ОГЭ», образовательный портал для подготовки к экзаменамhttps://math-oge.sdamgia.ru/test?theme=62
2) На одном из рисунков изображена гипербола. Укажите номер этого рисунка. 2
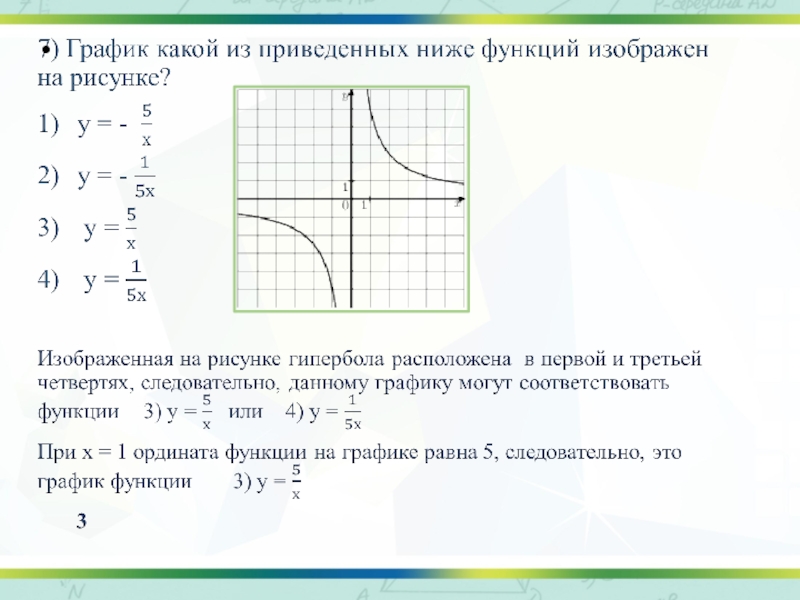
Слайд 53) График какой из приведенных ниже функций изображен на рисунке?
у =
х² - х,
у = - х² - х,
у = х² + х,
у = -х² + х,
Ветви изображённой на рисунке параболы направленны вверх, а абсцисса вершины отрицательна. Следовательно, данному графику могут соответствовать функции 1) у = х² - х или 3) у = х² + х.
Найдем абсциссы точек пересечения графиков данных функций с осью Ох, приравняв правые части к нулю
у = - х² - х,
у = х² + х,
у = -х² + х,
Ветви изображённой на рисунке параболы направленны вверх, а абсцисса вершины отрицательна. Следовательно, данному графику могут соответствовать функции 1) у = х² - х или 3) у = х² + х.
Найдем абсциссы точек пересечения графиков данных функций с осью Ох, приравняв правые части к нулю
3
Слайд 86) На одном из рисунков изображена гипербола.
Укажите номер этого рисунка.
На
первом рисунке изображена парабола.
На втором рисунке изображена гипербола.
На третьем рисунке изображена ветвь параболы.
На четвертом рисунке изображена линейная функция.
2
На втором рисунке изображена гипербола.
На третьем рисунке изображена ветвь параболы.
На четвертом рисунке изображена линейная функция.
2
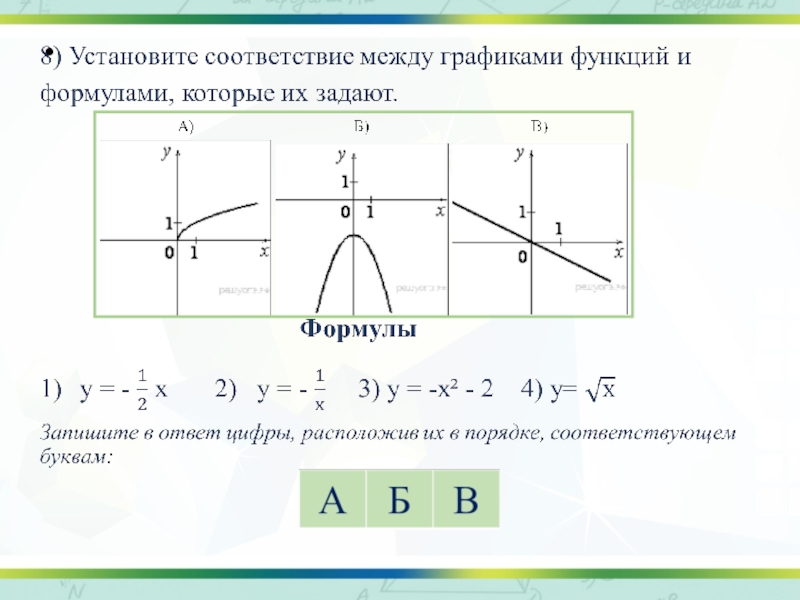
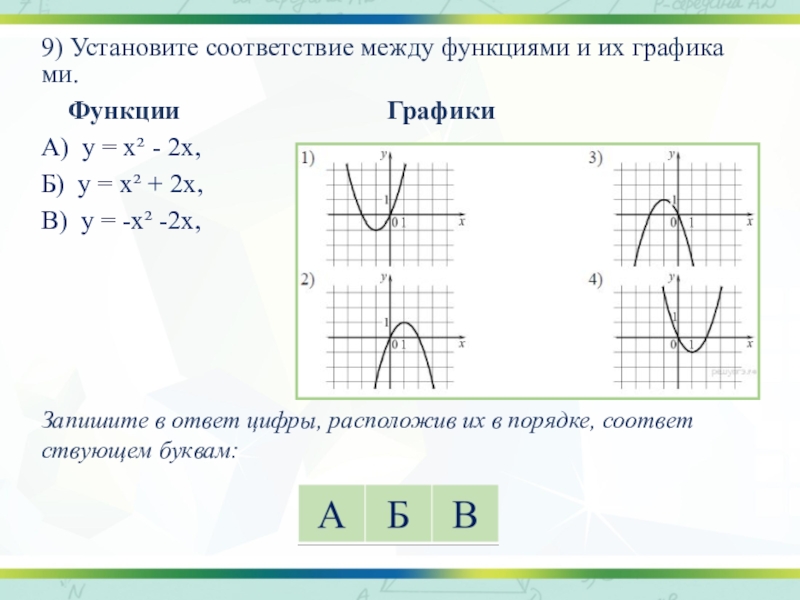
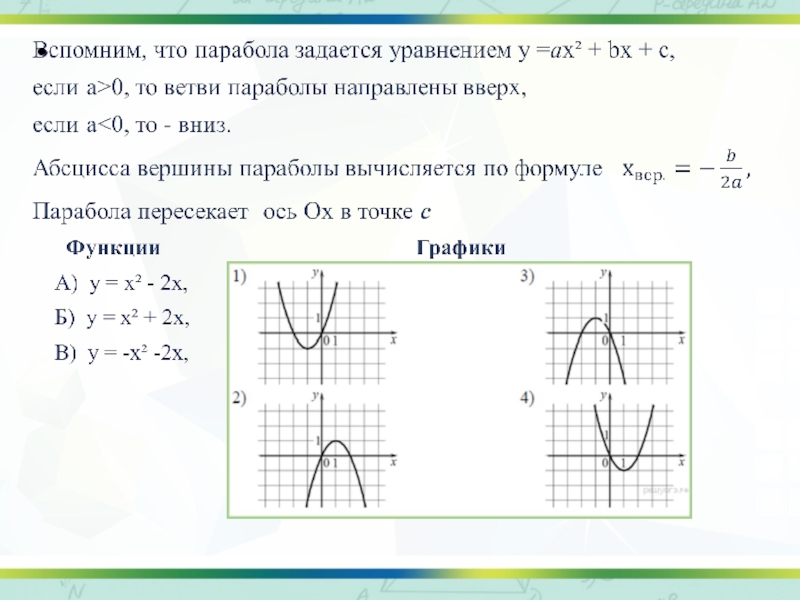
Слайд 129) Установите соответствие между функциями и их графиками.
Функции
Графики
А) у = х² - 2х,
Б) у = х² + 2х,
В) у = -х² -2х,
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А) у = х² - 2х,
Б) у = х² + 2х,
В) у = -х² -2х,
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
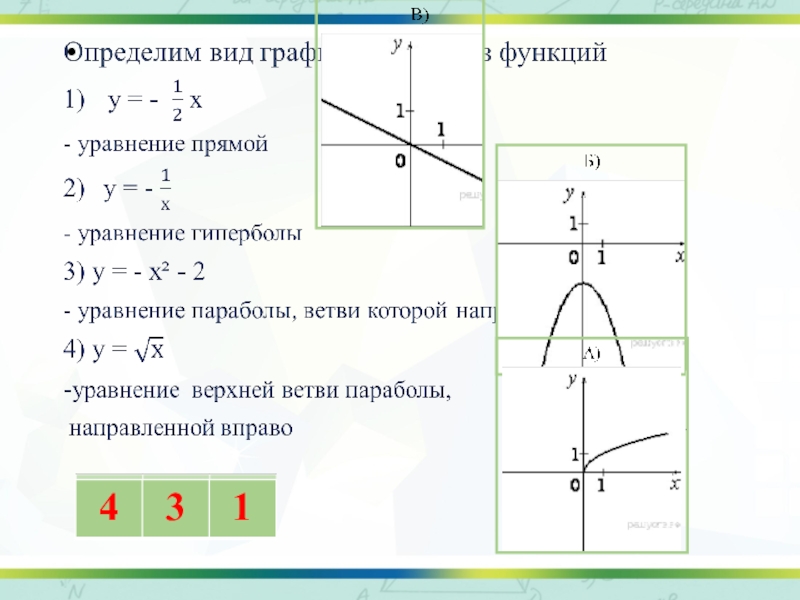
Слайд 14А) у = х² - 2х
ветви данной параболы направлены вверх,
абсцисса вершины параболы равна 1, она пересекает ось ординат в точке 0.
Б) у = х² +2х
ветви данной параболы направлены вверх, абсцисса вершины равна -1 , она пересекает ось ординат в точке 0.
В) у = -х² - 2х
ветви данной параболы направлены вниз, абсцисса вершины равна -1, она пересекает ось ординат в точке 0.
Б) у = х² +2х
ветви данной параболы направлены вверх, абсцисса вершины равна -1 , она пересекает ось ординат в точке 0.
В) у = -х² - 2х
ветви данной параболы направлены вниз, абсцисса вершины равна -1, она пересекает ось ординат в точке 0.
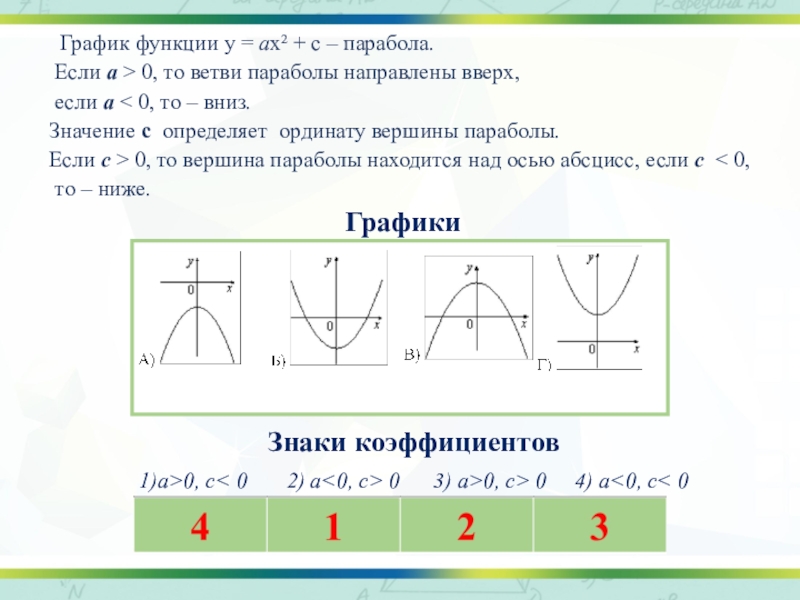
Слайд 1510) На рисунке изображены графики функций вида y = ax2 + c. Установите соответствие между
графиками и знаками коэффициентов a и c.
Графики
Знаки коэффициентов
а>0, с< 0 2) а<0, с> 0 3) а>0, с> 0 4) а<0, с< 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
Графики
Знаки коэффициентов
а>0, с< 0 2) а<0, с> 0 3) а>0, с> 0 4) а<0, с< 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам.
Слайд 16 График функции у = aх² + с – парабола.
Если
a > 0, то ветви параболы направлены вверх,
если a < 0, то – вниз.
Значение с определяет ординату вершины параболы.
Если с > 0, то вершина параболы находится над осью абсцисс, если с < 0,
то – ниже.
Графики
Знаки коэффициентов
1)а>0, с< 0 2) а<0, с> 0 3) а>0, с> 0 4) а<0, с< 0
если a < 0, то – вниз.
Значение с определяет ординату вершины параболы.
Если с > 0, то вершина параболы находится над осью абсцисс, если с < 0,
то – ниже.
Графики
Знаки коэффициентов
1)а>0, с< 0 2) а<0, с> 0 3) а>0, с> 0 4) а<0, с< 0
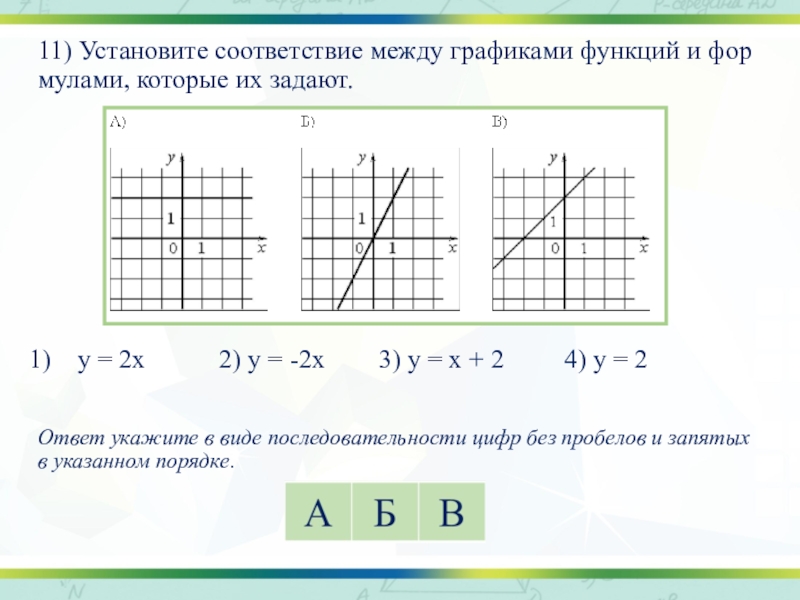
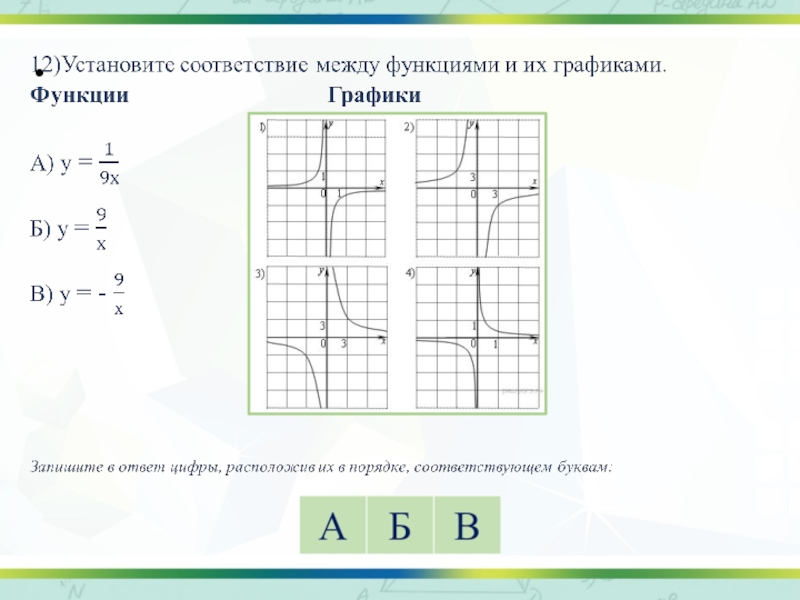
Слайд 1711) Установите соответствие между графиками функций и формулами, которые их задают.
у = 2х 2) у = -2х 3) у = х + 2 4) у = 2
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
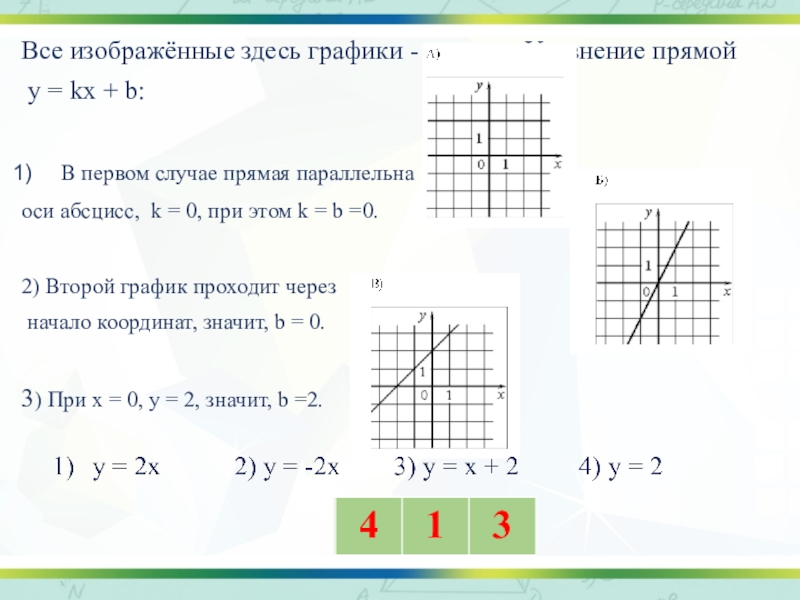
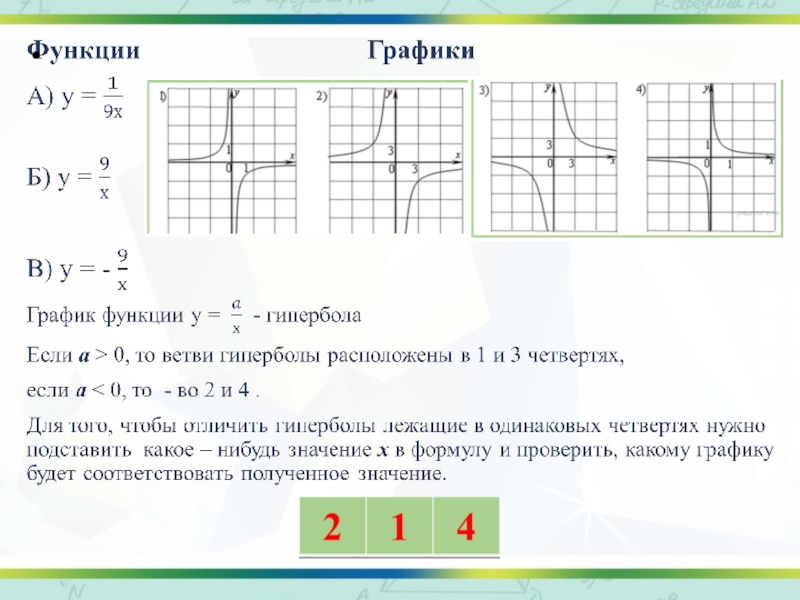
Слайд 18Все изображённые здесь графики - прямые. Уравнение прямой
у = kх
+ b:
В первом случае прямая параллельна
оси абсцисс, k = 0, при этом k = b =0.
2) Второй график проходит через
начало координат, значит, b = 0.
3) При х = 0, у = 2, значит, b =2.
В первом случае прямая параллельна
оси абсцисс, k = 0, при этом k = b =0.
2) Второй график проходит через
начало координат, значит, b = 0.
3) При х = 0, у = 2, значит, b =2.
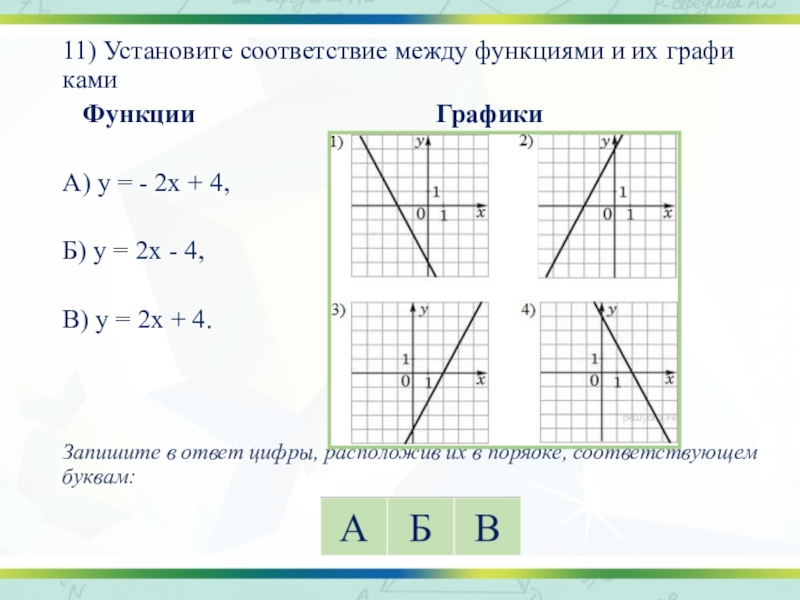
Слайд 1911) Установите соответствие между функциями и их графиками
Функции
Графики
А) у = - 2х + 4,
Б) у = 2х - 4,
В) у = 2х + 4.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А) у = - 2х + 4,
Б) у = 2х - 4,
В) у = 2х + 4.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Слайд 20Если прямая задана уравнением у = kх + b,
то при k > 0 функция возрастает, при k < 0 — убывает.
Значению b соответствует значение функции в точке х = 0
А) у = - 2х + 4,
уравнение задаёт убывающую функцию,
пересекающую ось ординат в точке 4.
Б) у = 2х - 4,
уравнение задаёт возрастающую функцию,
пересекающую ось ординат в точке −4.
В) у = 2х + 4.
уравнение задаёт возрастающую функцию,
пересекающую ось ординат в точке 4.
Значению b соответствует значение функции в точке х = 0
А) у = - 2х + 4,
уравнение задаёт убывающую функцию,
пересекающую ось ординат в точке 4.
Б) у = 2х - 4,
уравнение задаёт возрастающую функцию,
пересекающую ось ординат в точке −4.
В) у = 2х + 4.
уравнение задаёт возрастающую функцию,
пересекающую ось ординат в точке 4.
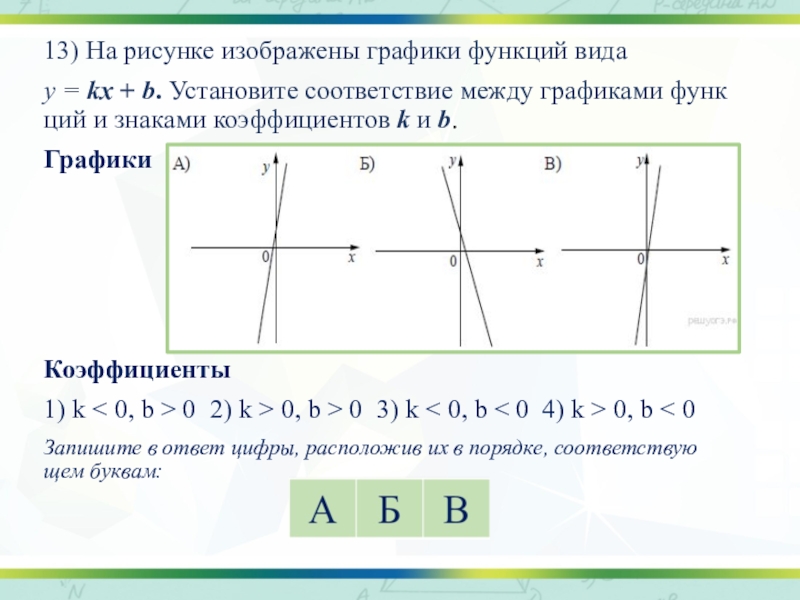
Слайд 2313) На рисунке изображены графики функций вида
y = kx +
b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
Коэффициенты
1) k < 0, b > 0 2) k > 0, b > 0 3) k < 0, b < 0 4) k > 0, b < 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Графики
Коэффициенты
1) k < 0, b > 0 2) k > 0, b > 0 3) k < 0, b < 0 4) k > 0, b < 0
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Слайд 24Графики
Коэффициенты
1) k < 0, b > 0 2) k > 0,
b > 0 3) k < 0, b < 0 4) k > 0, b < 0
Если прямая задана уравнением y = kx + b и k > 0, то функция возрастает, при k < 0 — убывает.
Значению b соответствует значение функции в точке х = 0.
Если прямая задана уравнением y = kx + b и k > 0, то функция возрастает, при k < 0 — убывает.
Значению b соответствует значение функции в точке х = 0.
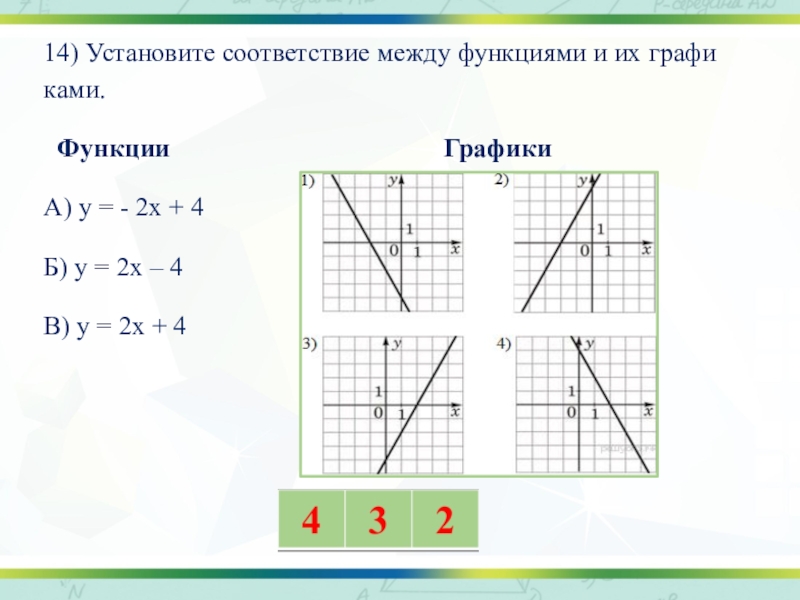
Слайд 2514) Установите соответствие между функциями и их графиками.
Функции
Графики
А) у = - 2х + 4
Б) у = 2х – 4
В) у = 2х + 4
А) у = - 2х + 4
Б) у = 2х – 4
В) у = 2х + 4