- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Простейшие тригонометрические уравнения(10класс)
Содержание
- 1. Презентация по математике на тему Простейшие тригонометрические уравнения(10класс)
- 2. Урок по теме «Простейшие тригонометрические уравнения» Цели
- 3. Немного истории…
- 4. На раннем этапе тригонометрия развивалась в тесной
- 5. Хотя название науки возникло сравнительно недавно, многие
- 6. Долгое время тригонометрия носила чисто геометрический характер,
- 7. Начиная с XVII в., тригонометрические функции начали
- 8. Аналитическая теория тригонометрических функций в основном была
- 9. Таким образом, тригонометрия, возникшая как наука о
- 10. ТЕСТЫ
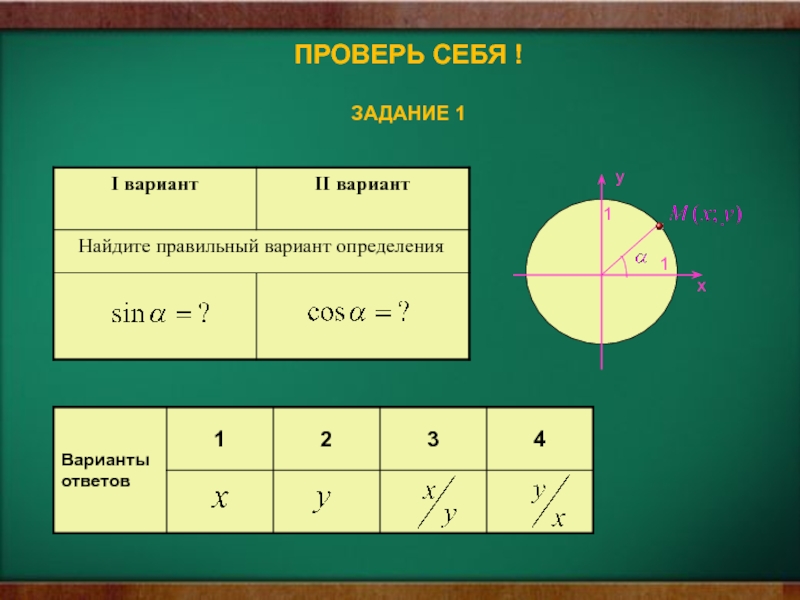
- 11. ПРОВЕРЬ СЕБЯ ! ЗАДАНИЕ 111xy
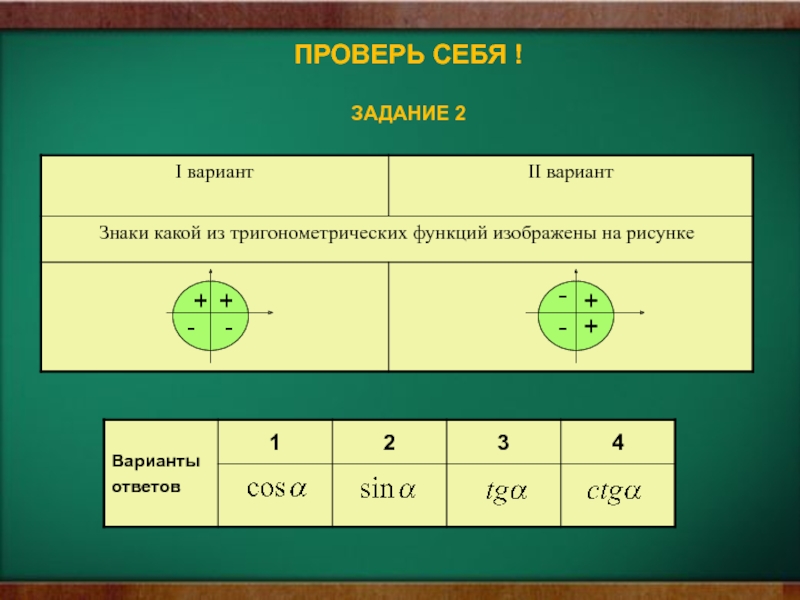
- 12. ПРОВЕРЬ СЕБЯ ! ЗАДАНИЕ 2
- 13. ПРОВЕРЬ СЕБЯ ! ЗАДАНИЕ 3
- 14. ПРОВЕРЬ СЕБЯ ! ЗАДАНИЕ 4
- 15. ПРОВЕРЬ СЕБЯ ! ЗАДАНИЕ 5
- 16. ПРОВЕРЬ СЕБЯ ! ЗАДАНИЕ 6
- 17. ПРОВЕРЬ СЕБЯ !
- 18. ++
- 19. .Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим. Примеры.ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
- 20. 1-1Решение уравнения Рассмотрим взаимное расположение графиков функций Простейшие тригонометрические уравнения
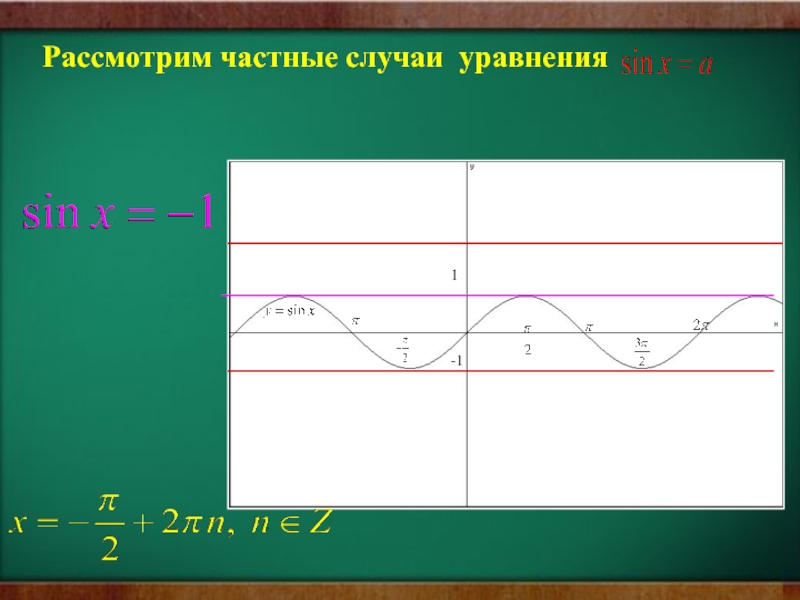
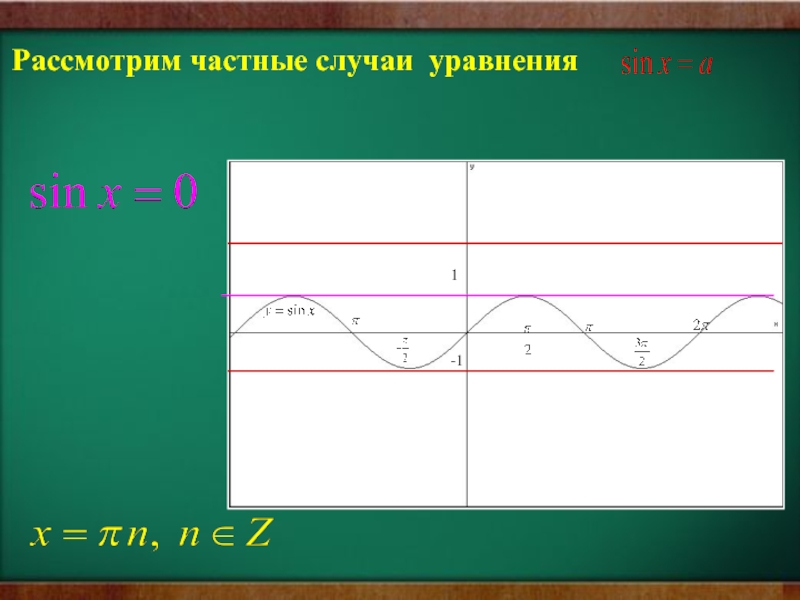
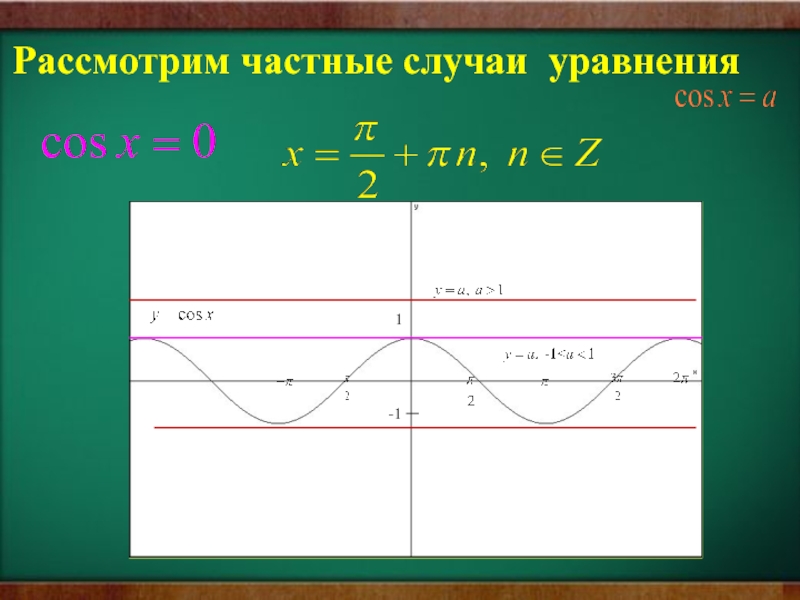
- 21. 1-1Рассмотрим частные случаи уравнения
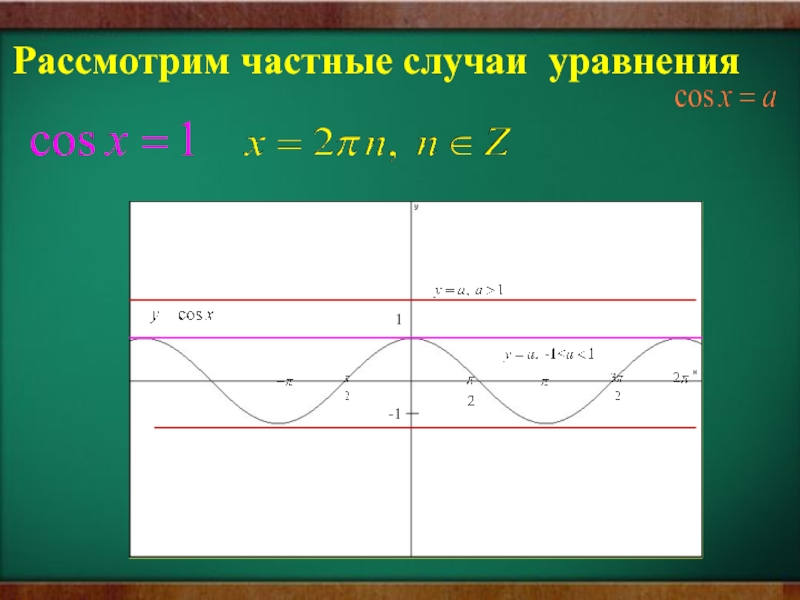
- 22. 1-1Рассмотрим частные случаи уравнения
- 23. 1-1Рассмотрим частные случаи уравнения
- 24. Систематизируем полученные результаты в таблицу
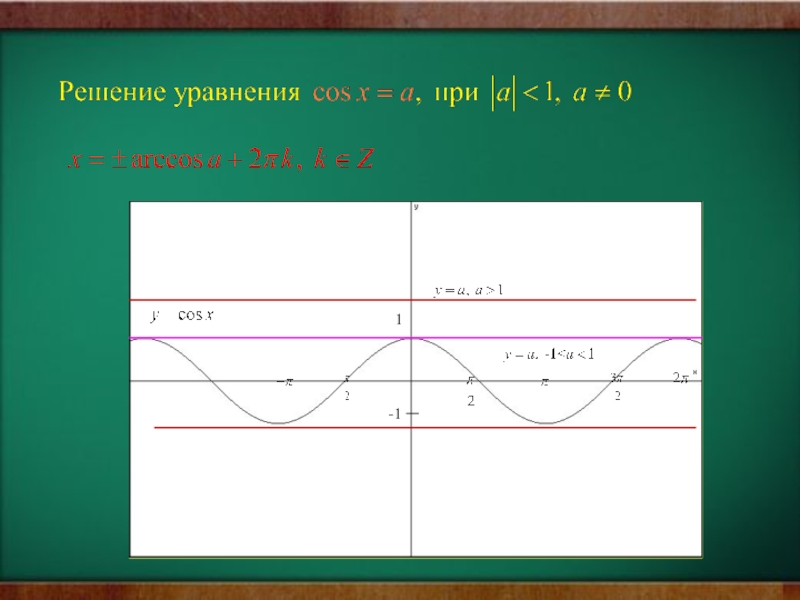
- 25. 1-1Решение уравнения при
- 26. Пример 1.Решение.Получаем частный случай, значитОтвет:Выразим из полученного равенства:Окончательно имеем
- 27. Пример 2.Решение.Применяя свойство нечетности синуса, получимСледовательно,Ответ:
- 28. 1-1Решение уравнения Как и в предыдущем случае
- 29. 1-1 Рассмотрим частные случаи уравнения
- 30. 1-1 Рассмотрим частные случаи уравнения
- 31. 1-1 Рассмотрим частные случаи уравнения
- 32. Занесем полученные результаты в таблицу
- 33. 1-1
- 34. Решение уравнений соs х =a.Имеет ли решения данные уравнения:
- 35. Делу время, потехе…Эту загадку задают детям при
- 36. Делу время, потехе…В 12-этажном доме есть лифт.
- 37. Слайд 37
- 38. Пример.Решение.Учитывая четность косинуса, получимСледовательно,Ответ:Решите уравнение
- 39. ТРИГОНОМЕТРИЧЕСКИЙТРЕНАЖЕР
- 40. Задание 1. Варианты ответов
- 41. НЕПРАВИЛЬНО!попробуйеще раз!
- 42. ПРАВИЛЬНО!
- 43. Варианты ответов
- 44. НЕПРАВИЛЬНО!попробуйеще раз!
- 45. ПРАВИЛЬНО!
- 46. Варианты ответов
- 47. НЕПРАВИЛЬНО!попробуйеще раз!
- 48. ПРАВИЛЬНО!Выход
- 49. Решение.ПРОДОЛЖИТЬЗадание 1.
- 50. ПРОДОЛЖИТЬЗадание 2. Решение.
- 51. Задание 3.Решение.Выход
Урок по теме «Простейшие тригонометрические уравнения» Цели УчебныеПовторить учебный материал, необходимый для успешного решения тригонометрических уравнений, рассмотреть методы решения простейших тригонометрических уравнений вида Воспитательные Организация совместных действий, ведущих к активизации учебного процесса, стимулирование учеников к
Слайд 2Урок по теме
«Простейшие тригонометрические уравнения»
Цели
Учебные
Повторить учебный материал,
необходимый для успешного решения тригонометрических уравнений,
рассмотреть методы решения простейших тригонометрических уравнений вида
Воспитательные
Организация совместных действий, ведущих к активизации учебного процесса,
стимулирование учеников к самооценке образовательной деятельности;
Воспитание чувства самопознания, самоопределения и самореализации;
развитие чувства ответственности и сопереживания.
Развивающие
Продолжить работу по развитию умений применять имеющиеся знания
при изучении нового материала
рассмотреть методы решения простейших тригонометрических уравнений вида
Воспитательные
Организация совместных действий, ведущих к активизации учебного процесса,
стимулирование учеников к самооценке образовательной деятельности;
Воспитание чувства самопознания, самоопределения и самореализации;
развитие чувства ответственности и сопереживания.
Развивающие
Продолжить работу по развитию умений применять имеющиеся знания
при изучении нового материала
Слайд 4 На раннем этапе тригонометрия развивалась в тесной связи с астрономией и
являлась её вспомогательным разделом.
Астрономы при нахождении расстояний до планет и звёзд использовали свойства треугольника.
Так возникла наука тригонометрия - наука об измерении треугольников, о выражении сторон через его углы.
Астрономы при нахождении расстояний до планет и звёзд использовали свойства треугольника.
Так возникла наука тригонометрия - наука об измерении треугольников, о выражении сторон через его углы.
Слайд 5Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии
понятия и факты были известны ещё две тысячи лет назад.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.
Слайд 6Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые
мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов.
Слайд 7Начиная с XVII в., тригонометрические функции начали применять к решению уравнений,
задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.
Слайд 8Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII
веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее, проще.
Слайд 9Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем
развилась и в науку о тригонометрических функциях.
Слайд 19.
Уравнение, содержащее неизвестное под знаком тригонометрической
функции, называется тригонометрическим.
Примеры.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Слайд 201
-1
Решение уравнения
Рассмотрим взаимное расположение графиков функций
Простейшие тригонометрические уравнения
Слайд 26Пример 1.
Решение.
Получаем частный случай, значит
Ответ:
Выразим из полученного равенства:
Окончательно имеем
Слайд 281
-1
Решение уравнения
Как и в предыдущем случае при
и при графики функций
и не имеют общих точек, следовательно
уравнение корней не имеет
и не имеют общих точек, следовательно
уравнение корней не имеет
Слайд 35Делу время, потехе…
Эту загадку задают детям при поступлении
в одну из
московских школ.
Если ребенок отвечает на нее - его определяют
в физико-математический класс.
Корова - 2
Овца - 2
Свинья - 3
Собака - 3
Кошка - 3
Утка - 3
Кукушка - 4
Петух - 8
Ослик - ?
Если ребенок отвечает на нее - его определяют
в физико-математический класс.
Корова - 2
Овца - 2
Свинья - 3
Собака - 3
Кошка - 3
Утка - 3
Кукушка - 4
Петух - 8
Ослик - ?
Слайд 36Делу время, потехе…
В 12-этажном доме есть лифт. На первом этаже
живет
всего 2 человека, от этажа к этажу
количество жильцов увеличивается вдвое.
Какая кнопка в лифте этого дома нажимается чаще других?
количество жильцов увеличивается вдвое.
Какая кнопка в лифте этого дома нажимается чаще других?
Из гнезда вылетели три ласточки. Какова вероятность того,
что через 15 секунд они будут
находиться в одной плоскости?