Багдуева Д.Л.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Подготовка к ЕГЭ, задание В8
Содержание
- 1. Презентация по математике на тему Подготовка к ЕГЭ, задание В8
- 2. Немного полезной информации Производная определяется как предел отношения
- 3. Производной функции в точке называют число, равное
- 4. Значение производной функции в точке x =
- 5. №1 На рисунке изображен график функции y =
- 6. Решение: По графику функции видно, что функция –
- 7. №2 Прямая y = 3x – 5 параллельна
- 8. Решение: Так как прямая y = 3x
- 9. № 3 Прямая y = - 4x +15
- 10. Решение: Угловой коэффициент касательной y = -
- 11. При x = 0: y = x³
- 12. № 4 На рисунке изображён график функции y
- 13. Решение: Целые точки – это точки с
- 14. № 5 На рисунке изображен график функции y=
- 15. Решение: Определяем на графике точку, у которой
- 16. №6 На рисунке изображен график функции y=f(x), определенной
- 17. Решение: Проведем прямую y = 3. Посчитаем
- 18. № 7 На рисунке изображен график функции y
- 19. Решение: Говоря образно, точки экстремума – это
- 20. № 8 Дан график производной функции y =
- 21. Решение: Касательная к графику функции y =
- 22. № 9 Дан график производной функции y
- 23. Решение: Функция возрастает на промежутках, в которых её
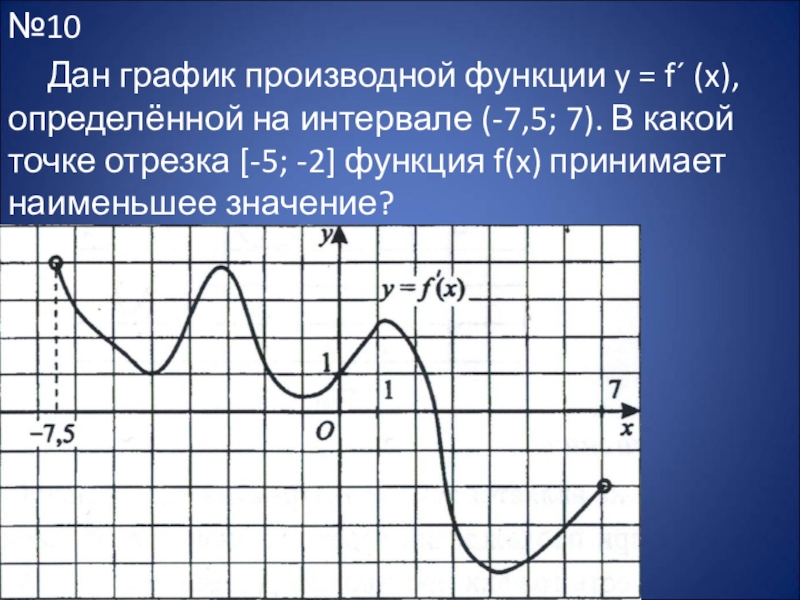
- 24. №10 Дан график производной функции y = f´
- 25. Решение: На отрезке [-5; -2] производная функции y
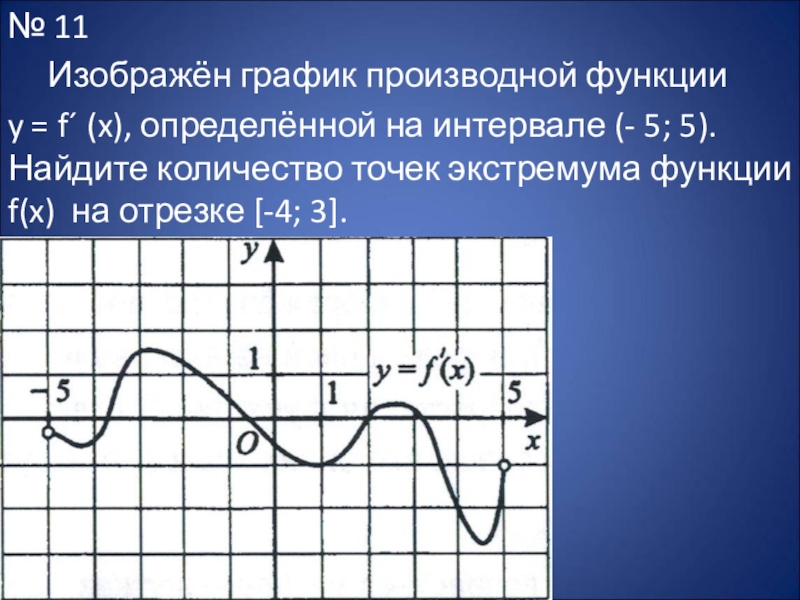
- 26. № 11 Изображён график производной функции y =
- 27. Решение: Точка является точкой экстремума непрерывной функции,
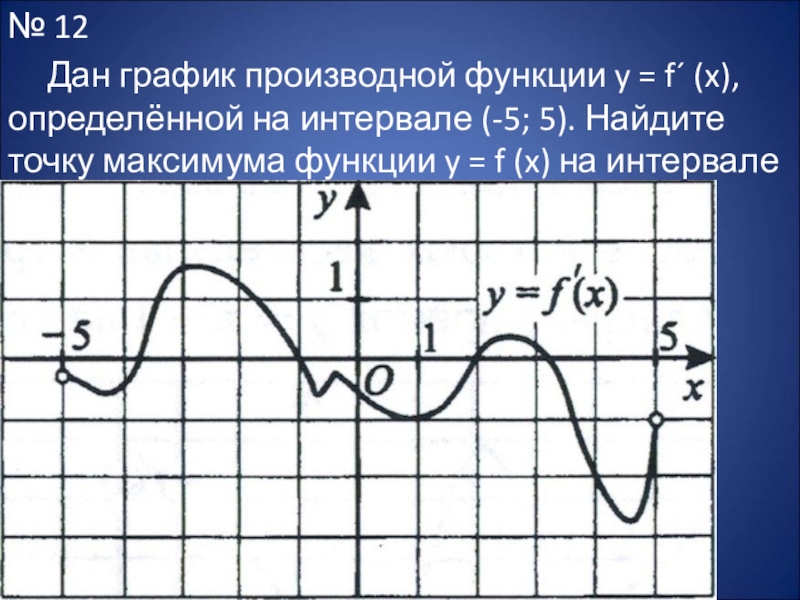
- 28. № 12 Дан график производной функции y =
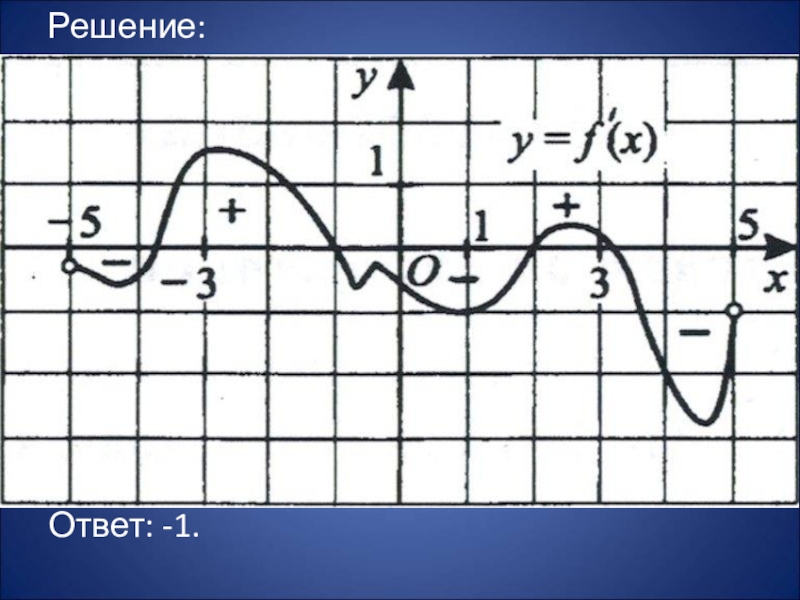
- 29. Решение: апм Ответ: -1.
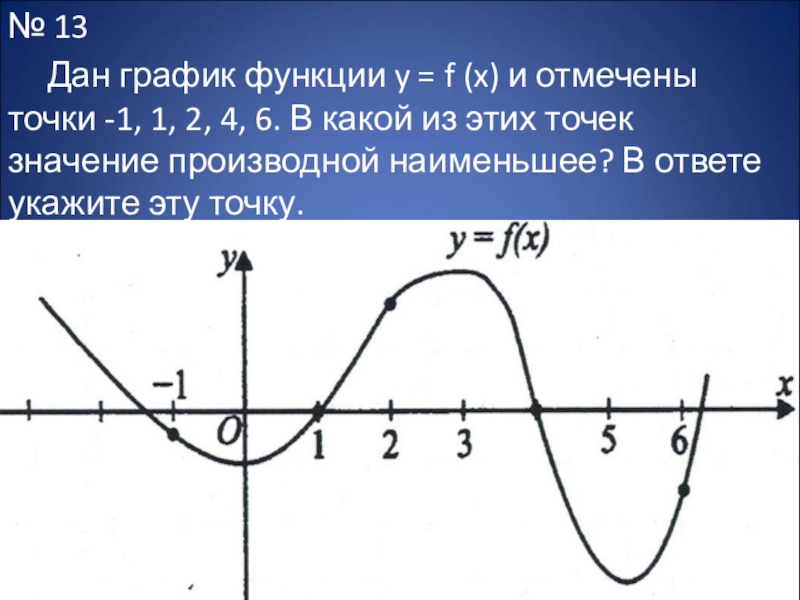
- 30. № 13 Дан график функции y = f
- 31. Решение: Значение производной в точке x˳ равно
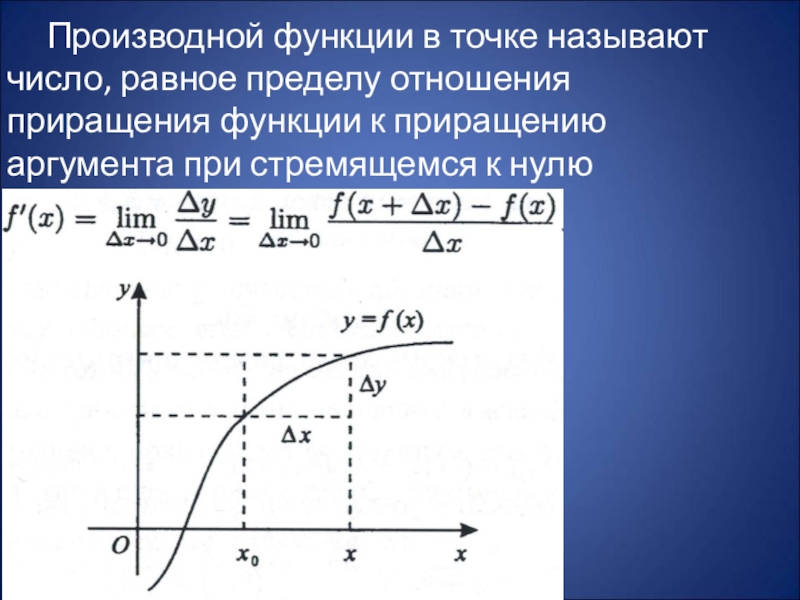
Немного полезной информации Производная определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Функцию, имеющую производную(в некоторой точке), называют дифференцируемой (в этой точке). Процесс вычисления производной называется дифференцированием. Производная так
Слайд 2Немного полезной информации
Производная определяется как предел отношения приращения функции к приращению
её аргумента при стремлении приращения аргумента к нулю. Функцию, имеющую производную(в некоторой точке), называют дифференцируемой (в этой точке). Процесс вычисления производной называется дифференцированием. Производная так же является функцией.
Слайд 3 Производной функции в точке называют число, равное пределу отношения приращения функции
к приращению аргумента при стремящемся к нулю приращении аргумента.
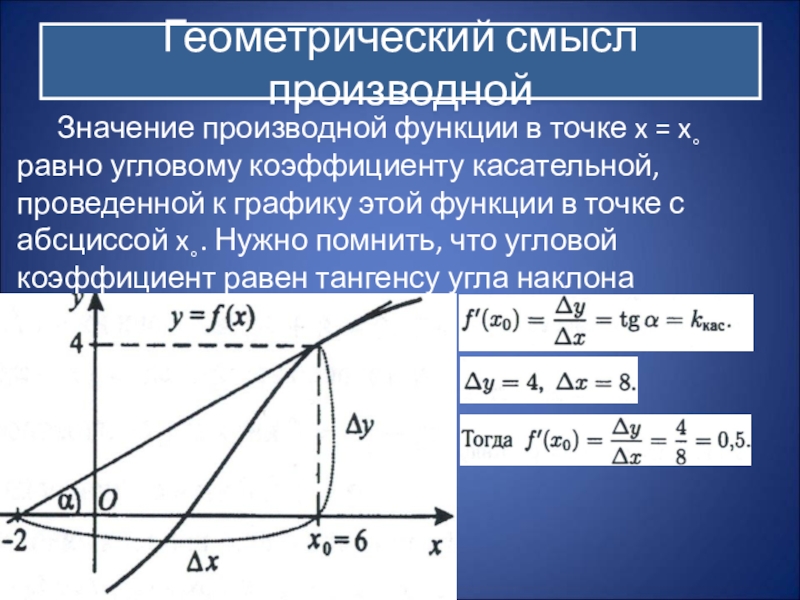
Слайд 4 Значение производной функции в точке x = x˳ равно угловому коэффициенту
касательной, проведенной к графику этой функции в точке с абсциссой x˳. Нужно помнить, что угловой коэффициент равен тангенсу угла наклона касательной.
Геометрический смысл производной
Слайд 5№1
На рисунке изображен график функции y = f(x) и касательная к
нему в точке с абсциссой x˳. Найдите значение производной функции f(x) в т.x˳ точке x˳.
Решение задач
Слайд 6Решение:
По графику функции видно, что функция – убывающая, поэтому знак производной
в точке касания «минус». Выберем две точки касательной.
Например, (-2; -9) и (-5; -3). Разность их абсцисс
Δ x = 3, разность ординат Δ y = 6. Делим Δ y на Δ x, получаем 6 : 3= 2, ставим знак «-».
Ответ: - 2.
Например, (-2; -9) и (-5; -3). Разность их абсцисс
Δ x = 3, разность ординат Δ y = 6. Делим Δ y на Δ x, получаем 6 : 3= 2, ставим знак «-».
Ответ: - 2.
Слайд 7№2
Прямая y = 3x – 5 параллельна касательной к графику функции
y = x ² +2x -7. Найдите абсциссу точки касания.
Слайд 8Решение:
Так как прямая y = 3x -5 параллельна касательной, то
угловой коэффициент касательной равен угловому коэффициенту прямой y = 3x – 5, то есть k = 3. Так как касательная проведена к графику функции y = x ² + 2x – 7, то значение производной в точке касания равно значению углового коэффициента касательной, то есть y´(x) = 3.
Найдём производную функции y = x ² + 2x – 7.
y´(x) = (x ² + 2x – 7) ´=2x +2. Из равенства y´(x) = 3 можно найти абсциссу точку касания.
2x +2 = 3
2x = 1
x = 0,5
Ответ: x = 0,5
Найдём производную функции y = x ² + 2x – 7.
y´(x) = (x ² + 2x – 7) ´=2x +2. Из равенства y´(x) = 3 можно найти абсциссу точку касания.
2x +2 = 3
2x = 1
x = 0,5
Ответ: x = 0,5
Слайд 9№ 3
Прямая y = - 4x +15 является касательной к графику
функции y = x³ + 3x² - 4x + 11. Найдите абсциссу точки касания.
Слайд 10Решение:
Угловой коэффициент касательной y = - 4x +15 равен -4.
Получим y´(x) = -4, где
y´(x) = (x³ + 3x² - 4x + 11) ´ = 3x² + 6x – 4.
3x² + 6x – 4 = - 4
3x² + 6x = 0
3x( x + 2 ) = 0
x = 0, или x = -2.
Мы получили два возможных значения для абсциссы точки касания. Выбрать одно из них можно, подставив найденные значения x в формулы функции и касательной. В точке касания значения функции и прямой должны совпасть.
y´(x) = (x³ + 3x² - 4x + 11) ´ = 3x² + 6x – 4.
3x² + 6x – 4 = - 4
3x² + 6x = 0
3x( x + 2 ) = 0
x = 0, или x = -2.
Мы получили два возможных значения для абсциссы точки касания. Выбрать одно из них можно, подставив найденные значения x в формулы функции и касательной. В точке касания значения функции и прямой должны совпасть.
Слайд 11При x = 0: y = x³ + 3x² - 4x
+ 11 = 0³ + 3 · 0² - 4 · 0 + 11 = 11
y кас = - 4x +15 = - 4 · 0 + 15 = 15
y (0) = 11
y кас (0) = 15.
Так как значения функции и касательной при x = 0 разные, абсцисса x = 0 нам не подходит.
Проверим при x = -2:
y = x³ + 3x² - 4x + 11 = (-2)³ + 3 · (- 2)² - 4 · (- 2) + 11= 23
y кас = - 4x +15 = - 4 · (- 2) + 15 = 8 + 15=23.
Значения функции и касательной при x = - 2 равны, значит, абсцисса точки касания x = - 2.
Ответ: - 2
y кас = - 4x +15 = - 4 · 0 + 15 = 15
y (0) = 11
y кас (0) = 15.
Так как значения функции и касательной при x = 0 разные, абсцисса x = 0 нам не подходит.
Проверим при x = -2:
y = x³ + 3x² - 4x + 11 = (-2)³ + 3 · (- 2)² - 4 · (- 2) + 11= 23
y кас = - 4x +15 = - 4 · (- 2) + 15 = 8 + 15=23.
Значения функции и касательной при x = - 2 равны, значит, абсцисса точки касания x = - 2.
Ответ: - 2
Слайд 12№ 4
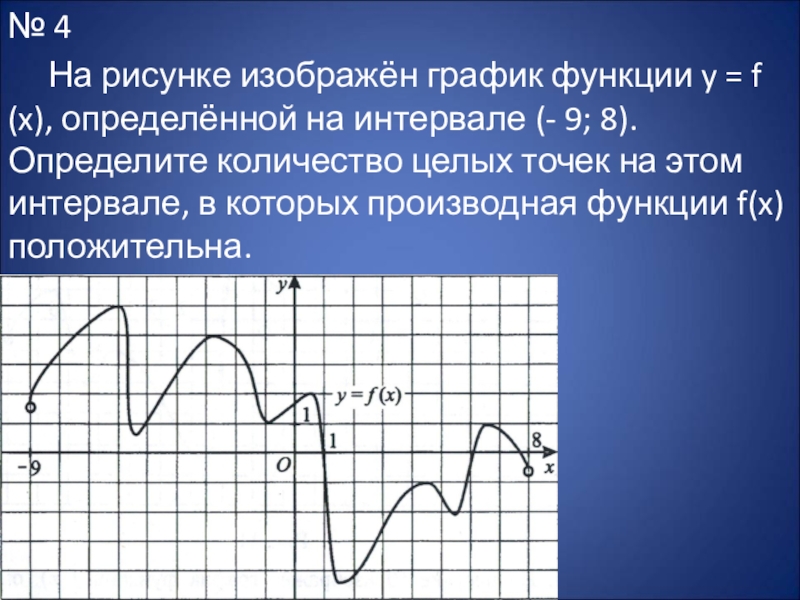
На рисунке изображён график функции y = f (x), определённой
на интервале (- 9; 8). Определите количество целых точек на этом интервале, в которых производная функции f(x) положительна.
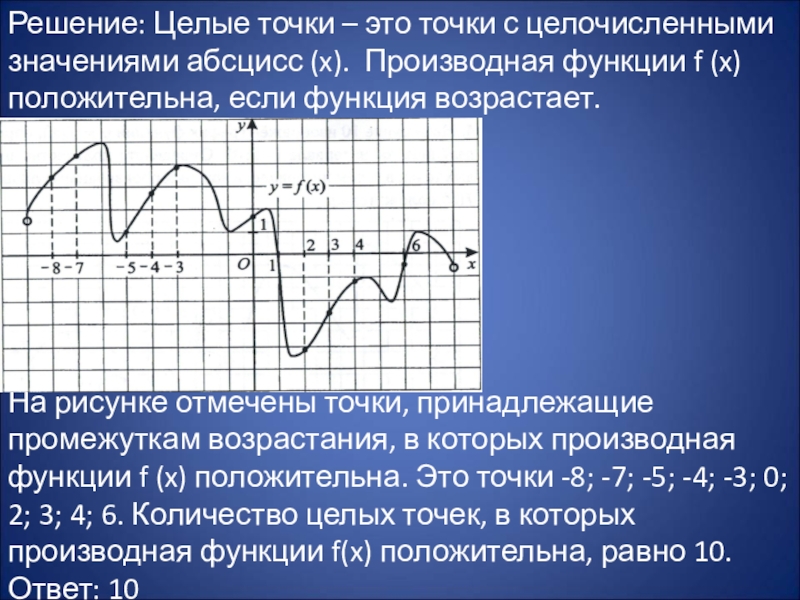
Слайд 13Решение: Целые точки – это точки с целочисленными значениями абсцисс (x).
Производная функции f (x) положительна, если функция возрастает.
На рисунке отмечены точки, принадлежащие промежуткам возрастания, в которых производная функции f (x) положительна. Это точки -8; -7; -5; -4; -3; 0; 2; 3; 4; 6. Количество целых точек, в которых производная функции f(x) положительна, равно 10. Ответ: 10
На рисунке отмечены точки, принадлежащие промежуткам возрастания, в которых производная функции f (x) положительна. Это точки -8; -7; -5; -4; -3; 0; 2; 3; 4; 6. Количество целых точек, в которых производная функции f(x) положительна, равно 10. Ответ: 10
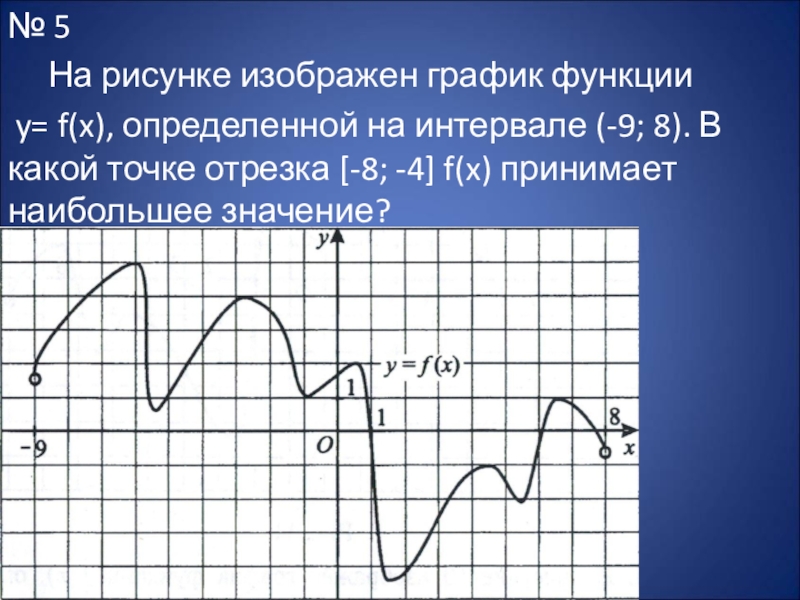
Слайд 14№ 5
На рисунке изображен график функции
y= f(x), определенной на
интервале (-9; 8). В какой точке отрезка [-8; -4] f(x) принимает наибольшее значение?
Слайд 15Решение:
Определяем на графике точку, у которой абсцисса x лежит на
отрезке [- 8; -4], а ордината y наибольшая из возможных, то есть эта точка «самая высокая». Для данного графика это точка
(-6; 5). Значит, f(x) принимает наибольшее значение в точке x = - 6.
Ответ: - 6
(-6; 5). Значит, f(x) принимает наибольшее значение в точке x = - 6.
Ответ: - 6
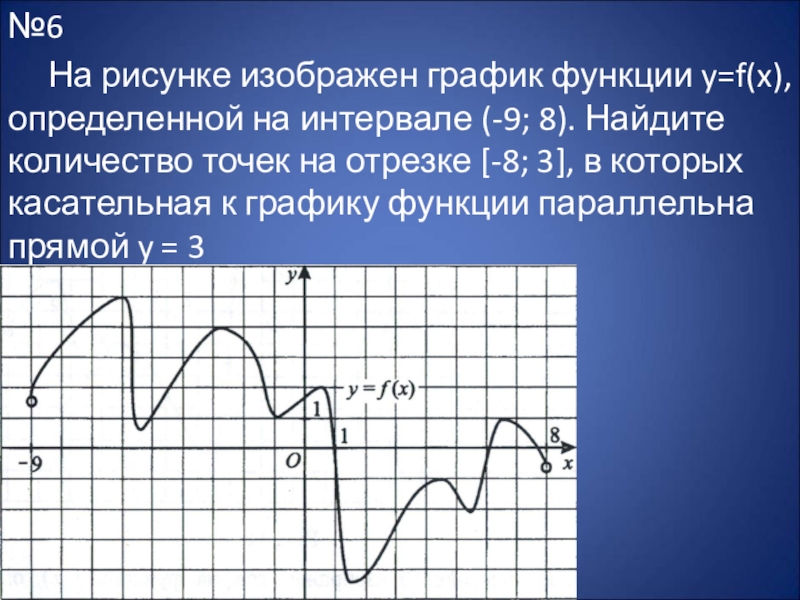
Слайд 16№6
На рисунке изображен график функции y=f(x), определенной на интервале (-9; 8).
Найдите количество точек на отрезке [-8; 3], в которых касательная к графику функции параллельна прямой y = 3
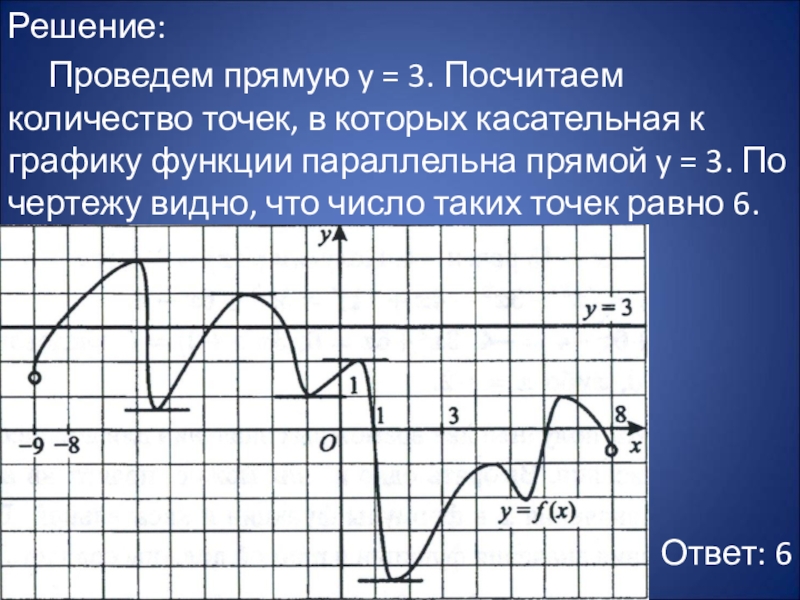
Слайд 17Решение:
Проведем прямую y = 3. Посчитаем количество точек, в которых
касательная к графику функции параллельна прямой y = 3. По чертежу видно, что число таких точек равно 6.
Ответ: 6
Ответ: 6
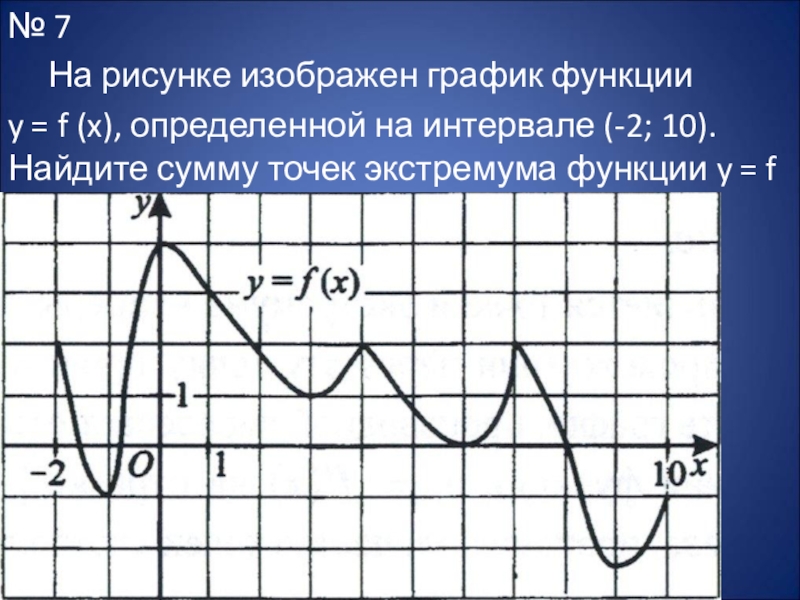
Слайд 18№ 7
На рисунке изображен график функции
y = f (x), определенной
на интервале (-2; 10). Найдите сумму точек экстремума функции y = f (x).
Слайд 19 Решение:
Говоря образно, точки экстремума – это те значения x, при
которых на графике видны «горбики» и «впадинки». Точками экстремума данной функции являются точки x = -1, x = 0, x = 3,
x = 4, x = 6, x = 7 и x = 9. Сумма точек экстремума функции y = f (x) равна -1+0+3+4+6+7+9=28
Ответ: 28
x = 4, x = 6, x = 7 и x = 9. Сумма точек экстремума функции y = f (x) равна -1+0+3+4+6+7+9=28
Ответ: 28
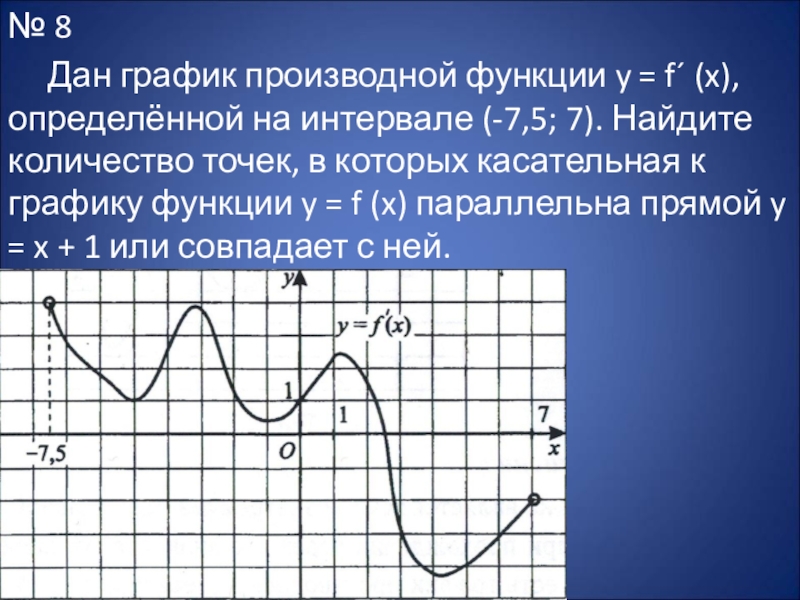
Слайд 20№ 8
Дан график производной функции y = f´ (x), определённой на
интервале (-7,5; 7). Найдите количество точек, в которых касательная к графику функции y = f (x) параллельна прямой y = x + 1 или совпадает с ней.
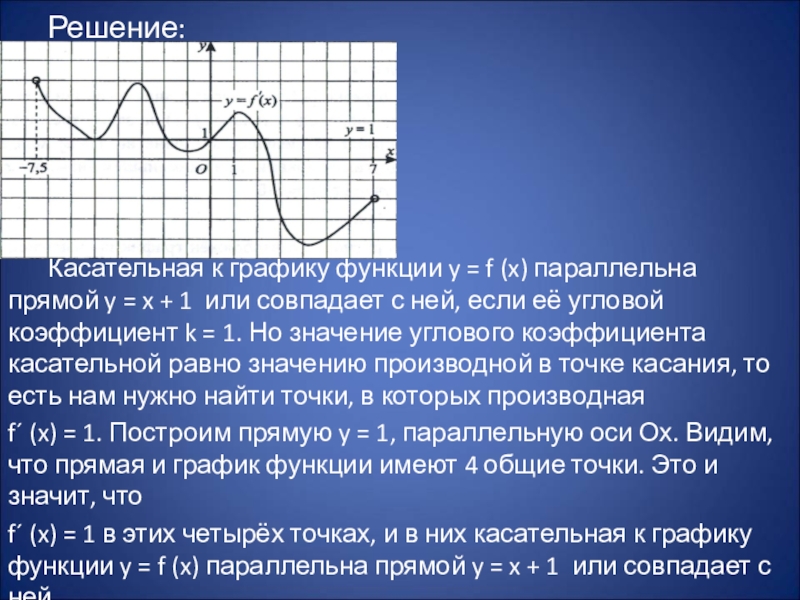
Слайд 21 Решение:
Касательная к графику функции y = f (x) параллельна прямой
y = x + 1 или совпадает с ней, если её угловой коэффициент k = 1. Но значение углового коэффициента касательной равно значению производной в точке касания, то есть нам нужно найти точки, в которых производная
f´ (x) = 1. Построим прямую y = 1, параллельную оси Ох. Видим, что прямая и график функции имеют 4 общие точки. Это и значит, что
f´ (x) = 1 в этих четырёх точках, и в них касательная к графику функции y = f (x) параллельна прямой y = x + 1 или совпадает с ней.
Ответ: 4
f´ (x) = 1. Построим прямую y = 1, параллельную оси Ох. Видим, что прямая и график функции имеют 4 общие точки. Это и значит, что
f´ (x) = 1 в этих четырёх точках, и в них касательная к графику функции y = f (x) параллельна прямой y = x + 1 или совпадает с ней.
Ответ: 4
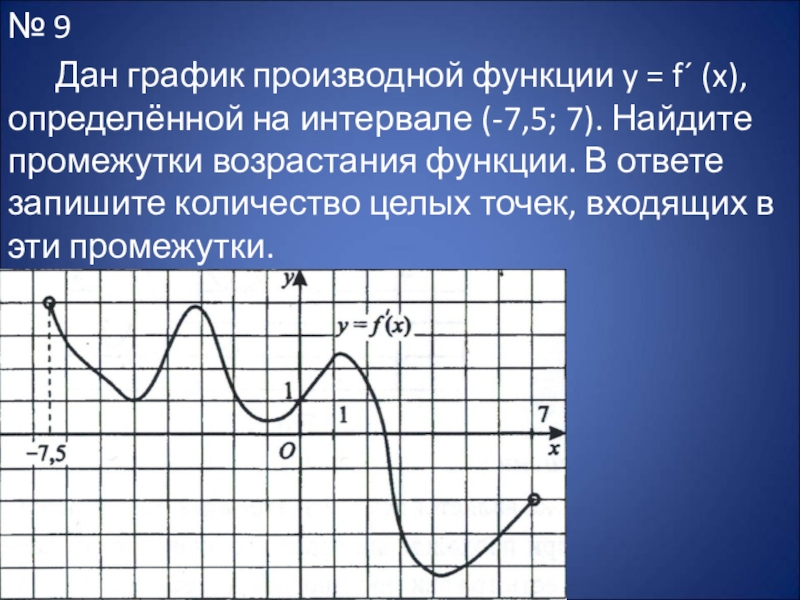
Слайд 22№ 9
Дан график производной функции y = f´ (x), определённой
на интервале (-7,5; 7). Найдите промежутки возрастания функции. В ответе запишите количество целых точек, входящих в эти промежутки.
Слайд 23 Решение:
Функция возрастает на промежутках, в которых её производная положительна. Найдем те
целые точки на графике, в которых производная положительна (лежит выше оси абсцисс Ох). Эти точки лежат в интервале от – 7, 5 до 2, 5. Целых среди них 10.
Ответ: 10
Ответ: 10
Слайд 24№10
Дан график производной функции y = f´ (x), определённой на интервале
(-7,5; 7). В какой точке отрезка [-5; -2] функция f(x) принимает наименьшее значение?
Слайд 25 Решение:
На отрезке [-5; -2] производная функции
y = f´ (x) положительна,
следовательно, f (x) на этом отрезке возрастает и принимает наименьшее значение на левом конце отрезка. В данном случае это x = - 5.
Ответ: - 5
Ответ: - 5
Слайд 26№ 11
Изображён график производной функции
y = f´ (x), определённой на
интервале (- 5; 5). Найдите количество точек экстремума функции f(x) на отрезке [-4; 3].
Слайд 27 Решение:
Точка является точкой экстремума непрерывной функции, если при прохождении через
эту точку производная меняет знак, то есть график производной пересекает ось абсцисс Ох. Производная функции y = f´ (x) на отрезке [-4; 3] меняет знак три раза, поэтому количество точек экстремума функции y = f(x) на данном промежутке равно 3.
Ответ: 3
Ответ: 3
Слайд 28№ 12
Дан график производной функции y = f´ (x), определённой на
интервале (-5; 5). Найдите точку максимума функции y = f (x) на интервале (-3; 3).
Слайд 30№ 13
Дан график функции y = f (x) и отмечены точки
-1, 1, 2, 4, 6. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
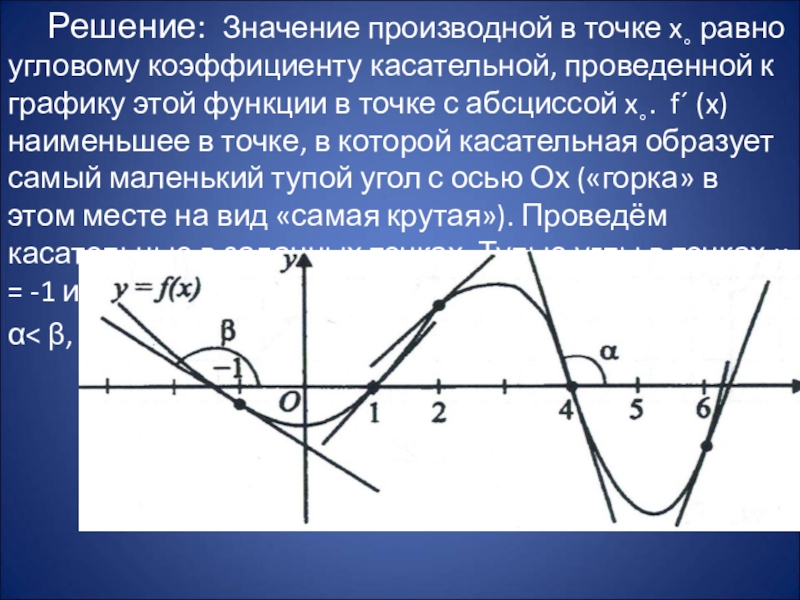
Слайд 31 Решение: Значение производной в точке x˳ равно угловому коэффициенту касательной, проведенной
к графику этой функции в точке с абсциссой x˳. f´ (x) наименьшее в точке, в которой касательная образует самый маленький тупой угол с осью Ох («горка» в этом месте на вид «самая крутая»). Проведём касательные в заданных точках. Тупые углы в точках x = -1 и x = 4.
α< β, значит, наименьшая производная в точке 4
α< β, значит, наименьшая производная в точке 4









![Презентация по математике на тему Подготовка к ЕГЭ, задание В8 Решение: Определяем на графике точку, у которой абсцисса x лежит на Решение: Определяем на графике точку, у которой абсцисса x лежит на отрезке [- 8; -4], а ордината](/img/tmb/8/700801/466f36c33cad816bcd0e4a383b5fe185-800x.jpg)


![Презентация по математике на тему Подготовка к ЕГЭ, задание В8 Решение: На отрезке [-5; -2] производная функции y = f´ (x) положительна, Решение: На отрезке [-5; -2] производная функции y = f´ (x) положительна, следовательно, f (x) на этом отрезке](/img/thumbs/d009bd7070829f726902a74b91acadb7-800x.jpg)