- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Неравенства
Содержание
- 1. Презентация по математике на тему Неравенства
- 2. Виды уравнений и неравенствРациональныеИррациональныеТригонометрическиеПоказательныеЛогарифмические
- 3. Рациональные уравненияУравнение вида P(x) = 0, где
- 4. Пример 1.3. 2x + 3 – 6(x
- 5. Квадратные уравненияУравнение вида ax²+ bx + c
- 6. Теорема Виета.Теорема 1 (Виета). Сумма корней квадратного
- 7. Пример Решить уравнение А)2x² + 5x –
- 8. Уравнение видаP1(x) / Q1(x) + P2(x) /
- 9. Решить уравнение (x³ – 27) / (x
- 10. Неравенства
- 11. Линейные неравенстваЛинейным неравенством с одной переменной х
- 12. Два неравенства f(х)
- 13. 2: а) обе части неравенства можно
- 14. 3.а) Обе части неравенства можно умножить или
- 15. Решите неравенство:
- 16. Квадратные неравенстваНеравенства вида
- 17. Алгоритм применения графического метода:1. Найти корни квадратного
- 18. Алгоритм выполнения метода интервалов:1. Разложить на множители
- 19. Решите неравенство: х2 – 6х + 8
- 20. Решение рационального неравенствасводится к решению эквивалентного неравенстваРn(х) × Qm(x) > 0,
- 21. Пример: Решить неравенствоРешение: Данное неравенство равносильно неравенствух²(х²
- 22. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯУравнение
- 23. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯКак правило
- 24. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯЗамечание. Иногда
- 25. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯПример.
- 26. Решите графически уравнение Решение: В одной системе
- 27. «Найди О.Д.З.» «Выполни замену»«Умножай на сопряжённое выражение»«Переходи к модулю»
- 28. Иррациональные неравенстваРешение иррациональных неравенств осложняется
- 29. Иррациональные неравенства
- 30. Ответ:
- 31. Пример-102х
- 32. Тригонометрическим уравнением называется уравнение, в котором переменная является аргументом одной или нескольких тригонометрических функций.
- 33. Основные типы тригонометрических уравненийОднородные тригонометрические уравнения первой
- 34. Простейшие тригонометрические уравнения sin x =
- 35. Решение уравнений с помощью формул sinx=a,
- 36. Слайд 36
- 37. Решить уравнение tg(3x- П/3)=-1
- 38. Однородные тригонометрические уравнения первой степениasin x +
- 39. Неоднородные тригонометрические уравнения первой степениasin x +
- 40. Однородные уравнения второй степени и уравнения, приводящиеся
- 41. Метод введения новой переменной
- 42. МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ.Решить уравнение 2sinxcos5x-cos5x=0.
- 43. Решить уравнение 2sin2x-5sinx+2=0.Решение.2sin 2x-5sinx+2=0sinx=t2t 2-5t+2=0t=2, t=1/2sinx=2,
- 44. Решение простейших тригонометрических неравенств
- 45. Простейшими тригонометрическими неравенствами называют неравенства вида
- 46. Рассмотрим решения неравенств вида:
- 47. Шаг 1yP(1;0)0x
- 48. Шаг 2yxP(1;0)0
- 49. Шаг 3yxP(1;0)0M2M1
- 50. Шаг 4yxP(1;0)0M1M2
- 51. Шаг 5yxP(1;0)0M2M1
- 52. Шаг 6yxP(1;0)0M2M1Р(1;0) -> М1 при повороте на
- 53. Шаг 7yxP(1;0)0M2M1Р(1;0) -> М1 при повороте на
- 54. Шаг 8yxP(1;0)0M2M1Р(1;0) -> М1 при повороте на
- 55. Шаг 9yxP(1;0)0M2M1Все решения данного неравенства – множество
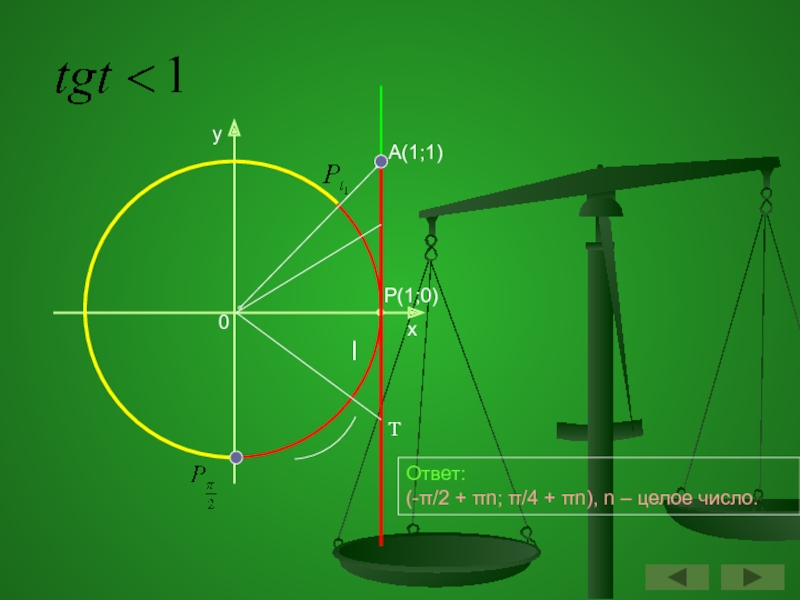
- 56. Решите неравенство
- 57. yxP(1;0)0А(1;1)ТlОтвет: (-π/2 + πn; π/4 + πn), n – целое число.
- 58. Алгоритм решения простейших тригонометрических неравенствПостроить единичную окружность.Отметить
- 59. Уравнения, содержащие переменную под знаком логарифма (в
- 60. Метод потенцированияРешить уравнение:Данное уравнение равносильно системе:Ответ: Ответ:
- 61. Использование определенияРешим уравнение:Решение.Ответ: 3
- 62. Приведение к квадратномуРешить уравнениеОтвет:Решение.
- 63. Метод логарифмированияРешить уравнениеРешение.Ответ: 0,1; 100
- 64. Метод введения новой переменнойРешить уравнениеРешениеПусть, тогдаУчитывая, чтоПолучим уравнениеОтвет: 16
- 65. Функционально-графический методРешить уравнениеРешение.Построим графики функцийY=lg x и y=xОтвет: корней нет.
- 66. Слайд 66
- 67. Если а>1, то функция y=log а
- 68. Если 0 < а< 1, то функция
- 69. Показательные уравненияУравнения видаНазывается показательным
- 70. Способы решения показательных уравнений -приведение степеней
- 71. Приведение к одному основаниюРазложение на множители
- 72. Подбор корня
- 73. Введение новой переменной9 х – 4*3 х
- 74. Решить неравенство При каких х график функции
- 75. Простейшие показательные неравенстваОпределение:Неравенство, содержащее неизвестную в показателе
- 76. Решение простейших показательных неравенствЗнак неравенстваСохраняетсяМеняется
- 77. Что нужно учесть при решении показательных неравенств
- 78. Решите неравенство-5
- 79. Решите неравенство
- 80. Литература.А.Г.Мордкович. Алгебра и начала анализа 10-11 класс.А.Н.Колмогоров.
Слайд 1Изучение уравнений и неравенств в школьном курсе математики.
Выполнила работу:
А.С. Рахметова
МОУ СОШ №1 с. Канглы
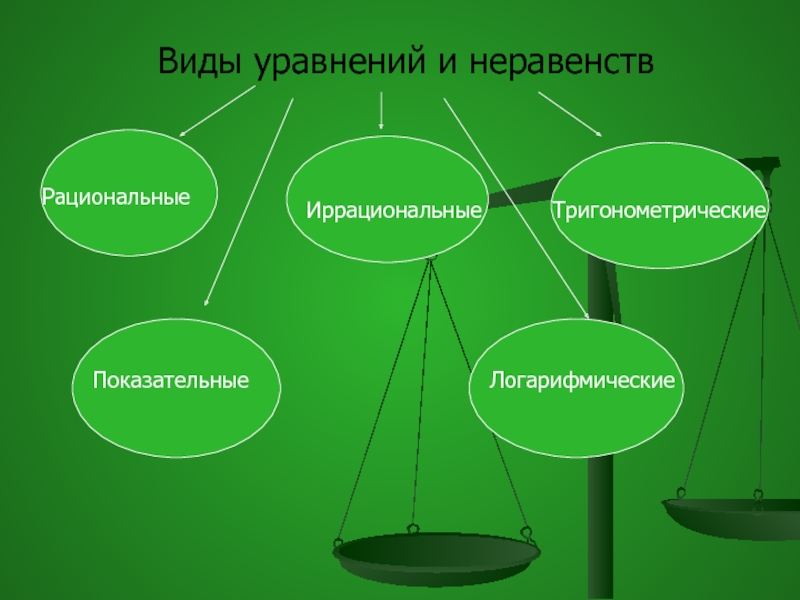
Слайд 2Виды уравнений и неравенств
Рациональные
Иррациональные
Тригонометрические
Показательные
Логарифмические
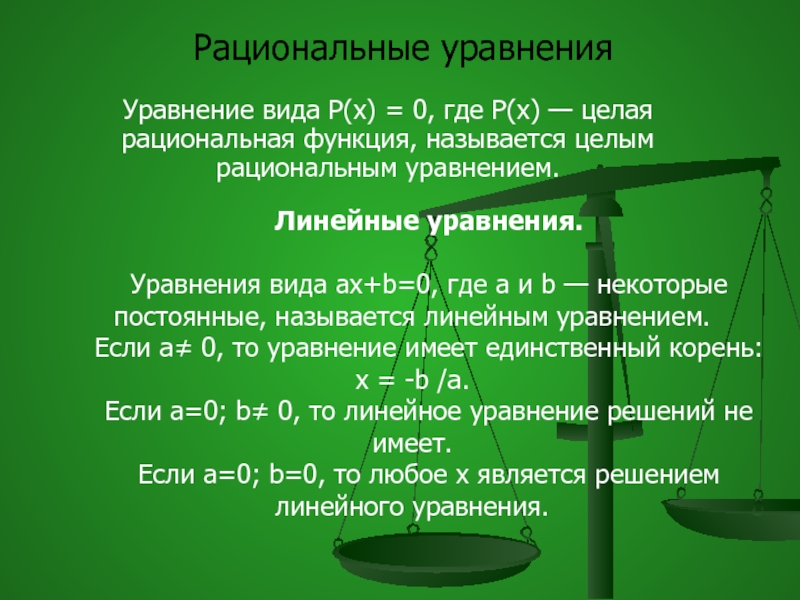
Слайд 3Рациональные уравнения
Уравнение вида P(x) = 0, где P(x) — целая рациональная
Линейные уравнения.
Уравнения вида ax+b=0, где a и b — некоторые постоянные, называется линейным уравнением.
Если a≠ 0, то уравнение имеет единственный корень: x = -b /a.
Если a=0; b≠ 0, то линейное уравнение решений не имеет.
Если a=0; b=0, то любое x является решением линейного уравнения.
Слайд 4Пример 1.3.
2x + 3 – 6(x – 1) = 4(x
Решение.
2x – 6x + 3 + 6 = 4 – 4x + 5,
– 4x + 9 = 9 – 4x,
-4x + 4x = 9 – 9,
0x = 0.
Ответ: Любое число.
Пример 1.1.
2x – 3 + 4(x – 1) = 5.
Решение.
2x – 3 + 4x – 4 = 5, 2x + 4x = 5 + 4 + 3,
6x = 12,
x = 2.
Ответ: 2.
Пример 1.2.
2x – 3 + 2(x – 1) = 4(x – 1) – 7.
Решение.
2x + 2x – 4x = 3 +2 – 4 – 7,
0x = – 6.
Ответ:Ø.
Слайд 5Квадратные уравнения
Уравнение вида ax²+ bx + c = 0, где a,
x — переменная, называется квадратным уравнением.
Формула решения квадратного уравнения.
для решения квадратного уравнения следует вычислить дискриминант
D = b²– 4ac.
Если D = 0, то квадратное уравнение имеет единственное решение:
X=-b / (2a).
Если D > 0, то квадратное уравнение имеет два корня:
X1=(-b + √D) / (2a); X2= (-b - √D) / (2a).
Если D < 0, то квадратное уравнение не имеет корней.
Слайд 6Теорема Виета.
Теорема 1 (Виета). Сумма корней квадратного уравнения равна коэффициенту при
Теорема 2 (обратная). Если выполняются равенства
X1 + X2 = – b / a и X1X2 = c / a,
то числа X1 и X2 являются корнями квадратного уравнения
ax² + bx + c = 0.
Слайд 7Пример
Решить уравнение
А)2x² + 5x – 1 = 0.
Решение
. D
X1 = (- 5 + √ 33) / 4; X2= (- 5 -√33) / 4.
Ответ: (- 5 + √33) / 4; (- 5 -√33) / 4.
Б) x2 -9x + 20 =0
x1 +x2 =9 и x1x2=20
x1=4 , x2=5.
Ответ : 4; 5.
Слайд 8Уравнение вида
P1(x) / Q1(x) + P2(x) / Q2(x) + … +
где P1(x), P2(x), … ,Pm(x), Q1(x), Q2(x), …, Qm(x) — целые рациональные функции, называется дробно- рациональным уравнением.
Решение дробно- рационального уравнения P (x) / Q (x) = 0, где
P (x) и Q (x) — многочлены (Q (x) ≠ 0), сводится к решению уравнения P (x) = 0 и проверке того, что корни удовлетворяют условию Q (x) ≠0.
Дробно-рациональные
Слайд 9Решить уравнение
(x³ – 27) / (x – 3) = 27
Решение.
Разложим числитель на множители (по формуле разности кубов):
(x – 3)(x² + 3x + 9) / (x – 3) = 27 .
Отсюда:
Квадратное уравнение x²+ 3 x – 18 = 0 имеет корни X1 = 3; X2 = -6
(X1 не входит в область допустимых значений).
Ответ: -6
Слайд 11Линейные неравенства
Линейным неравенством с одной переменной х называется неравенство вида ах
Решение неравенства – значение переменной х, которое обращает неравенство в верное числовое неравенство.
Множество частных решений называют общим решением.
Слайд 12Два неравенства f(х)
Правила
(преобразования неравенств, приводящие к равносильным неравенствам):
1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком (не меняя при этом знака неравенства)
Например: 3х + 5 < 7х
3х + 5 -7х < 0
Слайд 13 2: а) обе части неравенства можно умножить или разделить на
б) если обе части неравенства умножить или разделить на одно и то же выражение, положительное при любых значениях переменной, и сохранить знак неравенства, то получится неравенство, равносильное данному.
Например: а)8х – 12 > 4х2
2х – 3 > х2
б)(2х + 1)(х2 + 2) < 0
2х + 1< 0
Слайд 143.а) Обе части неравенства можно умножить или разделить на одно и
б) если обе части неравенства умножить или разделить на одно и то же выражение, отрицательное при всех значениях переменной, и изменить знак исходного неравенства на противоположный, то получится неравенство, равносильное данному.
Например: а) - 6х3 + 3х – 15 < 0
2х3 – х + 5 > 0
б) (3х – 4 )(-х2 – 2) > 0
3х – 4 < 0
Слайд 15Решите неравенство:
Решение: 5х + 6х – 3 >13х – 1
5х + 6х – 13х > 3 – 1
-2х > 2
х < -1
Ответ: (-∞; -1)
Слайд 16Квадратные неравенства
Неравенства вида
ах2 + bх + с > 0, где а ≠ 0, а,b,с - некоторые числа, называются квадратными.
Слайд 17Алгоритм применения графического метода:
1. Найти корни квадратного трехчлена ах2+bх+с, т.е. решить
2.Отметить найденные значения на оси х в координатной плоскости.
3. Схематично построить график параболы.
4. Записать ответ в соответствии со знаком неравенства.
Частные случаи при D < 0:
а) а < 0, ах2 + bх + с ≥ 0 нет решений
ах2 + bх + с < 0 (-∞;+∞)
б) а > 0 ах2 + bх + с > 0 (-∞;+∞)
ах2 + bх + с ≤ 0 нет решений
Слайд 18Алгоритм выполнения метода интервалов:
1. Разложить на множители квадратный трехчлен, используя формулу
2. Отметить на числовой прямой корни х1 и х2.
3. Определить знак выражения а(х-х1)(х-х2) на каждом из получившихся промежутков.
4. Записать ответ, выбрав промежутки с соответствующим знаку неравенства знаком
(если знак неравенства <,то выбираем промежутки со знаком «-», если знак неравенства >, то выбираем промежутки со знаком «+»).
Слайд 19Решите неравенство: х2 – 6х + 8 > 0
Решение: Разложим квадратный
х2 – 6х + 8 = 0
Д = 36 – 32 = 4, 4>0, два корня
х1,2 = (6 ± 2) : 2 х1 = 4, х2 = 2
х2 – 6х + 8 = (х – 2)(х - 4)
Отметим на числовой прямой корни трехчлена 2 и 4.Определим знаки выражения (х-2)(х-4) на каждом из промежутков.
+ 2 - 4 +
Ответ: х<2,х>4 или (-∞;2)U(4;+∞).
Слайд 20Решение рационального неравенства
сводится к решению эквивалентного неравенства
Рn(х) × Qm(x) > 0,
Слайд 21Пример:
Решить неравенство
Решение:
Данное неравенство равносильно неравенству
х²(х² – х – 2)
Множество решений последнего неравенства находится методом интервалов: ( -1;0)U(0;2).
Ответ: (-1;0) U(0;2).
Слайд 22 ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Уравнение A (x) = B
Примерами таких уравнений могут служить
Уравнение же
Рационально, поскольку в нём x не находится под знаком корня.
Понятия корня уравнения и его решения для иррациональных уравнений определяют так же, как и для рациональных.
Слайд 23 ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Как правило , иррациональное уравнение сводится
системе, содержащей уравнения и неравенства.
Пример.
Слайд 24 ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
Замечание. Иногда иррациональное уравнение можно свести
приведённому виду с помощью введения новой переменной.
Пример.
Первое уравнение совокупности не имеет корней, корень второго уравнения
х = 8.
Слайд 26
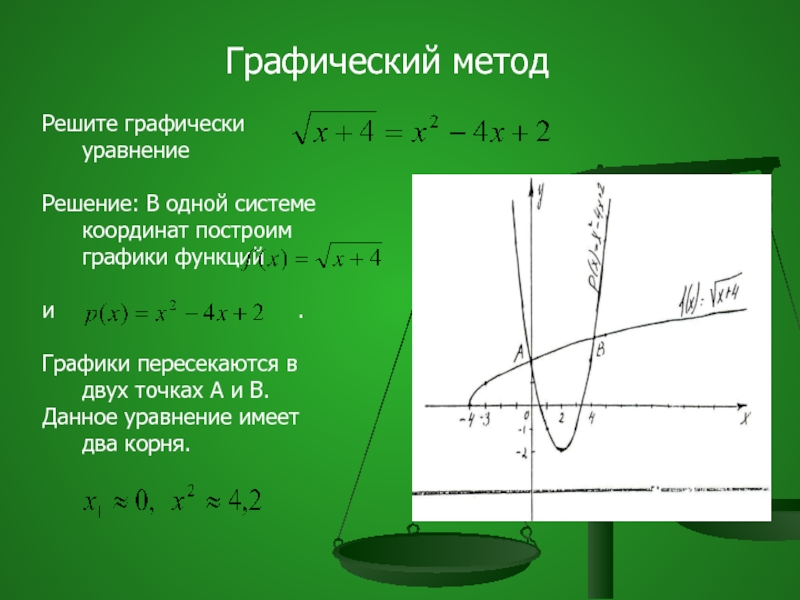
Решите графически уравнение
Решение: В одной системе координат построим графики функций
и .
Графики пересекаются в двух точках А и В.
Данное уравнение имеет два корня.
Графический метод
Слайд 28 Иррациональные неравенства
Решение иррациональных неравенств осложняется тем
обстоятельством, что неравенства A
An (x) < Bn (x) не являются равносильными:
Ведь только для неотрицательных чисел a и b из a < b
следует an < bn , а из an < bn следует a < b.
Поэтому при решении иррациональных неравенств надо
учитывать знаки его левой и правой частей.
Как правило , иррациональное неравенство сводится
к равносильной системе ( или совокупности систем ) неравенств.
Слайд 32Тригонометрическим уравнением
называется уравнение, в котором переменная является аргументом одной или
Слайд 33Основные типы тригонометрических уравнений
Однородные тригонометрические уравнения первой степени
Неоднородные тригонометрические уравнения первой
Однородные уравнения второй степени и уравнения, приводящиеся к ним
Уравнения, приводящиеся к квадратному относительно функции sin x или cos x
Слайд 35Решение уравнений с помощью формул
sinx=a,
x=(-1) n arcsina +Пn. x=± arccos a+2Пn.
sinx=0 cosx=0
x=Пn. x=П/2+ Пn.
sinx=1 cosx=1
x=П /2+ 2Пn. x=2Пn.
sinx=-1 cosx=-1
x= - П/2+2Пn. x=П+2Пn.
tgx=a x=arctg a+Пn.
Слайд 36 Решить уравнение
Решение.
2cos2x=-1
cos2x=-1/2
2x=+(п-arccos1/2)+2Пn
2x=+(П-П/3)+2Пn
2x=+2П/3+2Пn
x=+П/3+Пn, n-целое число.
Ответ: +П/3+Пn, n - целое число.
Слайд 37 Решить уравнение tg(3x- П/3)=-1
tg(3x-П/3)=-1
3x-П/3=-arctg1+Пn
3x-П/3=-П/4+Пn
3x=-П/4+П/3+Пn
3x=П/12+Пn
x=П/36+Пn/3, n- целое число.
Ответ: П/36+Пn/3, n-целое число.
Слайд 38Однородные тригонометрические уравнения первой степени
asin x + bcos x = 0
а≠0, b≠0.
Делением на cos x такое уравнение сводится к линейному уравнению относительно tg x. При использовании этого приема не происходит потери решения, хотя ОДЗ при таком преобразовании сужается.
Слайд 39Неоднородные тригонометрические уравнения первой степени
asin x + bcos x = c
а≠0, b≠0.
При решении уравнений такого вида применяется метод вспомогательного угла.
Слайд 40Однородные уравнения второй степени и уравнения, приводящиеся к ним
а sin²x+b sin
а≠0, с≠0.
Делением на cos²x ≠ 0 это уравнение приводится к квадратному относительно функции tg x :
a tg²x + b tgx + c = 0.
Слайд 41Метод введения новой переменной
tgx/2+3ctgx/ 2=4.
y+3/y=4,
y2+3=4y,
y2-4y+3=0,
y=1, y=3.
tgx/2=1 или tgx/2=3
x=П/2+2Пn; x=2arctg3+2Пn,
n-целое число
Ответ: x= П/2+2Пn, x=2arctg3+2Пn
Слайд 42МЕТОД РАЗЛОЖЕНИЯ НА МНОЖИТЕЛИ.
Решить уравнение 2sinxcos5x-cos5x=0.
Решение.
2sinxcos5x-cos5x=0
cos5x(2sinx-1)=0
cos5x=0;
5x=П/2+Пn; x=(-1)n П/6+Пn,
x=П/10+Пn/5; x=(-1)n П/6+Пn, -целое число.
Ответ:x=П/10+Пn/5, x=(-1)n П/6+Пn, -целое число.
Слайд 43Решить уравнение 2sin2x-5sinx+2=0.
Решение.
2sin 2x-5sinx+2=0
sinx=t
2t 2-5t+2=0
t=2, t=1/2
sinx=2, sinx=1/2.
Уравнение sinx=2 не имеет
sinx=1/2
X=(-1) n П/6+Пn, n-целое число.
Ответ: (-1) n П/6+Пn, n-целое число.
Слайд 52
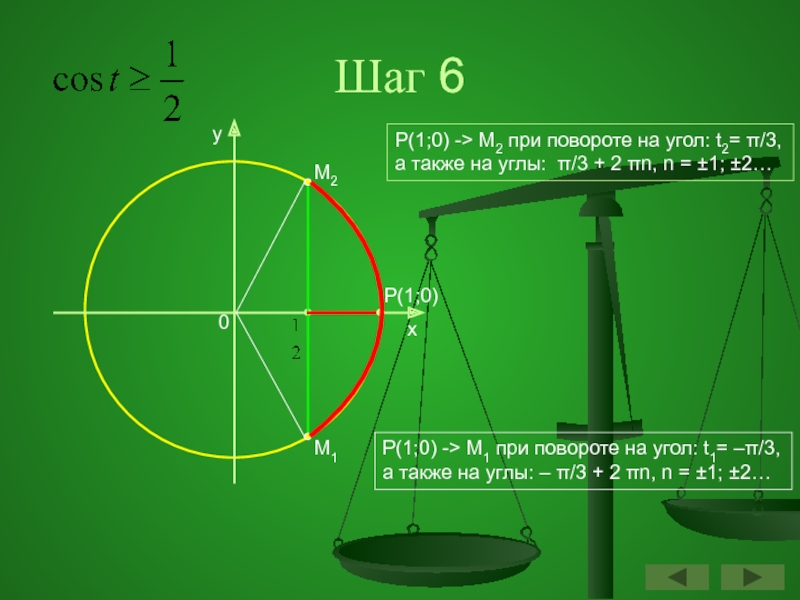
Шаг 6
y
x
P(1;0)
0
M2
M1
Р(1;0) -> М1 при повороте на угол: t1= –π/3,
а также
Р(1;0) -> М2 при повороте на угол: t2= π/3,
а также на углы: π/3 + 2 πn, n = ±1; ±2…
Слайд 53
Шаг 7
y
x
P(1;0)
0
M2
M1
Р(1;0) -> М1 при повороте на угол: t1= –π/3,
а также
Р(1;0) -> М2 при повороте на угол: t2= π/3,
а также на углы: π/3 + 2 πn, n = ±1; ±2…
-π/3 ≤ t ≤ π/3
Слайд 54
Шаг 8
y
x
P(1;0)
0
M2
M1
Р(1;0) -> М1 при повороте на угол: t1= –π/3,
а также
Р(1;0) -> М2 при повороте на угол: t2= π/3,
а также на углы: π/3 + 2 πn, n = ±1; ±2…
Все решения данного неравенства – множество промежутков
-π/3 + 2πn ≤ t ≤ π/3 + 2πn,
n – целое число.
-π/3 ≤ t ≤ π/3
Слайд 55
Шаг 9
y
x
P(1;0)
0
M2
M1
Все решения данного неравенства – множество промежутков
-π/3 + 2πn
n – целое число.
Ответ: -π/3 + 2πn ≤ t ≤ π/3 + 2πn, n – целое число.
Ответ: [-π/3 + 2πn; π/3 + 2πn], n – целое число.
Слайд 58Алгоритм решения простейших тригонометрических неравенств
Построить единичную окружность.
Отметить число а на соответствующей
- Провести прямую, проходящую через данную точку и перпендикулярную оси, на которой она расположена
(sin t, cos t).
- Провести луч из начала координат через полученную точку
(tg t).
Отметить точки пересечения прямой с окружностью.
Определить дугу, точки которой удовлетворяют заданному неравенству.
Найти значение углов поворота, соответствующих полученным точкам.
Записать ответ, учитывая область значений, область определения и периодичность функции.
Слайд 59
Уравнения, содержащие переменную под знаком логарифма (в частности, в основании логарифма),
Логарифмические уравнения
Решение этих уравнений основано на следующей теореме.
Теорема 1. Уравнение равносильно системе
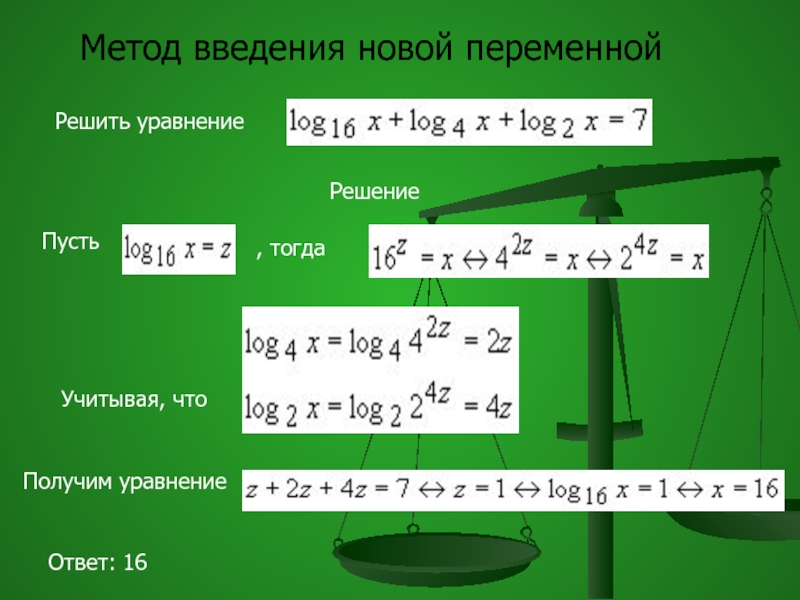
Слайд 64Метод введения новой переменной
Решить уравнение
Решение
Пусть
, тогда
Учитывая, что
Получим уравнение
Ответ: 16
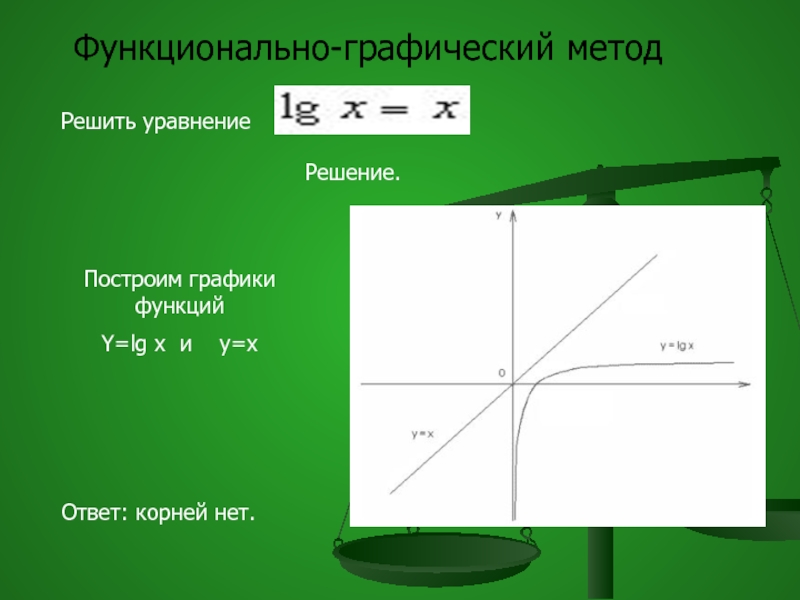
Слайд 65Функционально-графический метод
Решить уравнение
Решение.
Построим графики функций
Y=lg x и y=x
Ответ: корней нет.
Слайд 67 Если а>1, то функция y=log а x возрастающая, значит,
f(x)>a b (знак исходного неравенства сохраняется)
f(x)>0 (ОДЗ)
Пример: log 2 (7x+1)>3.
Данное неравенство равносильно системе:
( Основание логарифма а=2>1, знак неравенства сохраняем.)
7х + 1> 23,
7х + 1>0;
7х > 7 ,
7х > -1;
х > 1,
х > - 1/7.
Ответ: (1; ∞).
Логарифмические неравенства
Слайд 68Если 0 < а< 1, то функция y=log a x
f(x) < ab (знак исходного неравенства меняется)
f(x)>0 (ОДЗ)
Пример: log 0,2 (4x+5)>-2.
Данное неравенство равносильно системе:
4x+5< (0,2) -2,
4x+5>0 ;
4х< 25 – 5,
4х > -5;
х< 5,
х > - 1,25.
Ответ: (- 1,25; 5).
Слайд 70
Способы решения показательных уравнений
-приведение степеней к одному основанию в
-разложение на множители;
-введение новой переменной;
-деление на степень;
-графический способ;
-оценивание частей уравнения;
-подбор корня.
Слайд 73Введение новой переменной
9 х – 4*3 х +3 = 0
3 2х
t= 3 х
t2- 4*t+ 3 = 0
t1+ t2= 4 и t1*t2=3
t1=1 , t2=3
3х=1 или 3х= 3
Х= 0 , х= 1
Ответ: 0; 1
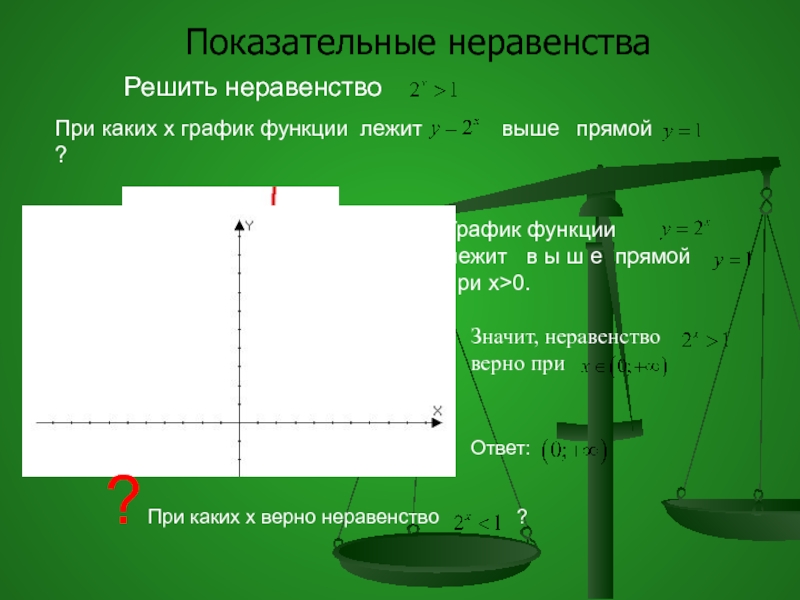
Слайд 74
Решить неравенство
При каких х график функции лежит
выше
График функции лежит в ы ш е прямой
при x>0.
Значит, неравенство верно при
Ответ:
? При каких х верно неравенство ?
Показательные неравенства
Слайд 75Простейшие показательные неравенства
Определение:
Неравенство, содержащее неизвестную в показателе степени, называется показательным неравенством.
Определение:
Неравенство
называется простейшим показательным неравенством.
Слайд 77Что нужно учесть при решении показательных неравенств ?
Решить неравенство
? Что
показательных неравенств ?
1. Привести основания степени к одинаковому основанию
2. Использовать свойства монотонной функции
Слайд 80Литература.
А.Г.Мордкович. Алгебра и начала анализа 10-11 класс.
А.Н.Колмогоров. Алгебра и начала анализа
Н.Я.Виленкин. Алгебра и математический анализ 9, 10 класс.
Ф.Ф.Лысенко. Тематические тесты 10-11 класс. Часть 1.
Т.А.Корешкова. Математика. ЕГЭ. Типовые тестовые задания. Издательство «Экзамен» 2009г.
А.Г. Цыпкин. Справочник по методам решения задач по математике. Москва, изд. «Наука», 1989г.
В.В. Вавилов. Задачи по математике. Уравнения и неравенства. Москва, изд. «Наука», 1987г.
Интернет-ресурсы.
www.wiki.ruwww.wiki.ruwww.school.ru
www.a-nomalia.narod.ru
www.egypet-best.ru
www.pyramids.ru