- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике8класс на тему Абсолютная и относительная погрешности
Содержание
- 1. Презентация по математике8класс на тему Абсолютная и относительная погрешности
- 2. На сколько отличаются полученные значения?По графику
- 3. Абсолютной погрешностью называется модуль разности точного и
- 4. Абсолютной погрешностью или, короче, погрешностью приближенного числа
- 5. Пример 1. На предприятии 1284 рабочих и
- 6. Слайд 6
- 7. Погрешность и точность измерения.
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
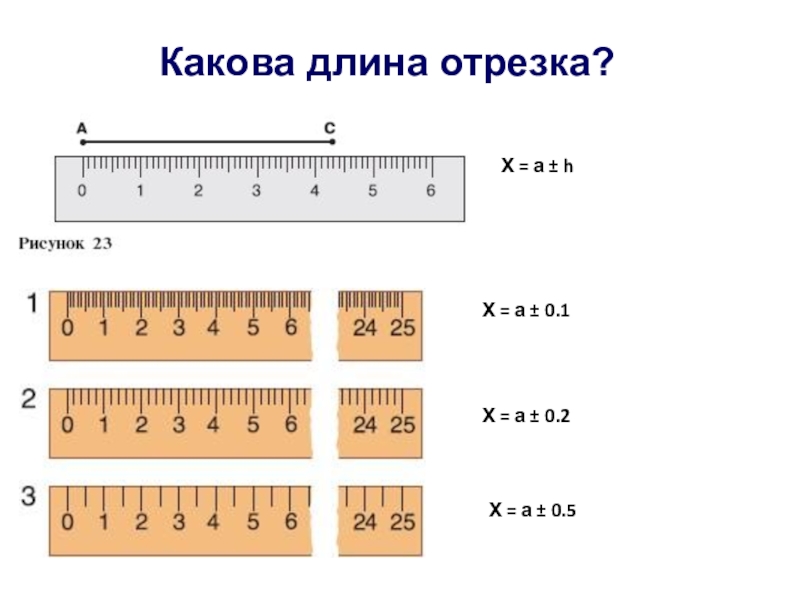
- 11. Какова длина отрезка?Х = а ± hХ
- 12. Если а приближённое значение числа х
- 13. Слайд 13
- 14. Слайд 14
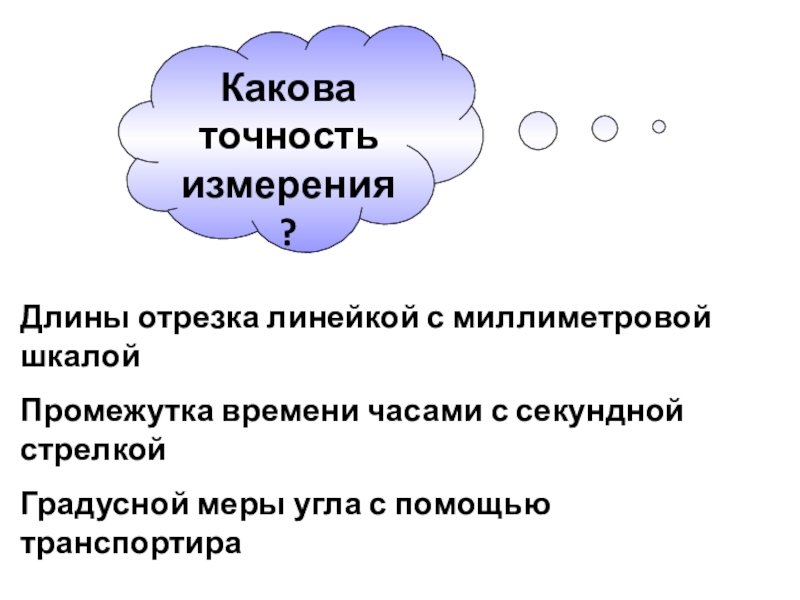
- 15. Длины отрезка линейкой с миллиметровой шкалойПромежутка времени
- 16. Слайд 16
- 17. Слайд 17
- 18. Какие из значений величин точные, какие приближенные:Толщина
- 19. Слайд 19
- 20. Слайд 20
- 21. Относительная погрешность Относительной погрешностью приближенного числа называется
- 22. Пример В школе 1254 учащихся.
- 23. Задача. Продавец взвешивает арбуз на чашечных
- 24. В большинстве случаев невозможно узнать точное значение
- 25. Слайд 25
- 26. Слайд 26
- 27. История созданияРазработка РСЗО «Град» началась еще в
- 28. Задание №791
- 29. Слайд 29
- 30. Слайд 30
Слайд 2
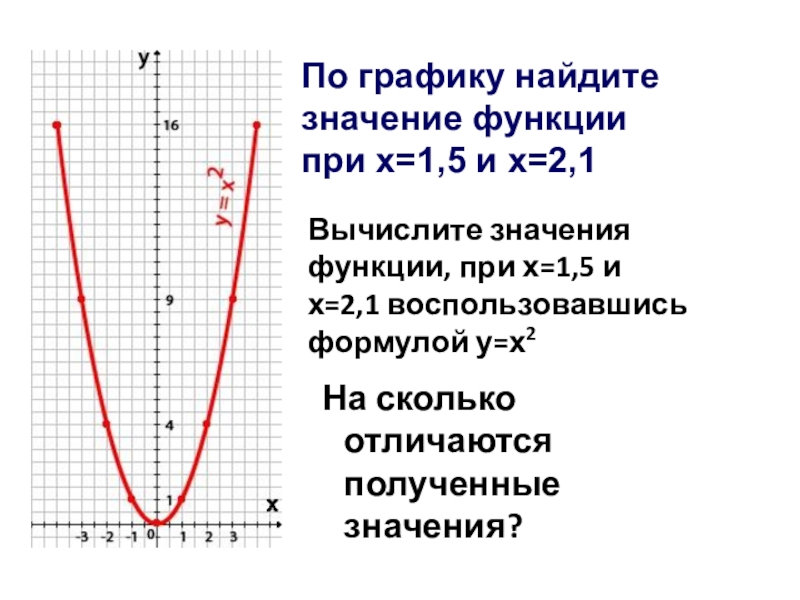
На сколько отличаются полученные значения?
По графику найдите значение функции
Вычислите значения функции, при х=1,5 и х=2,1 воспользовавшись формулой у=х2
Слайд 3Абсолютной погрешностью называется модуль разности точного и приближенного значений числа.
Х-
а- приближённое значение числа.
Абс.погр=/ Х—а /
Слайд 4Абсолютной погрешностью или, короче, погрешностью приближенного числа называется разность между этим
Слайд 5Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого
Слайд 7
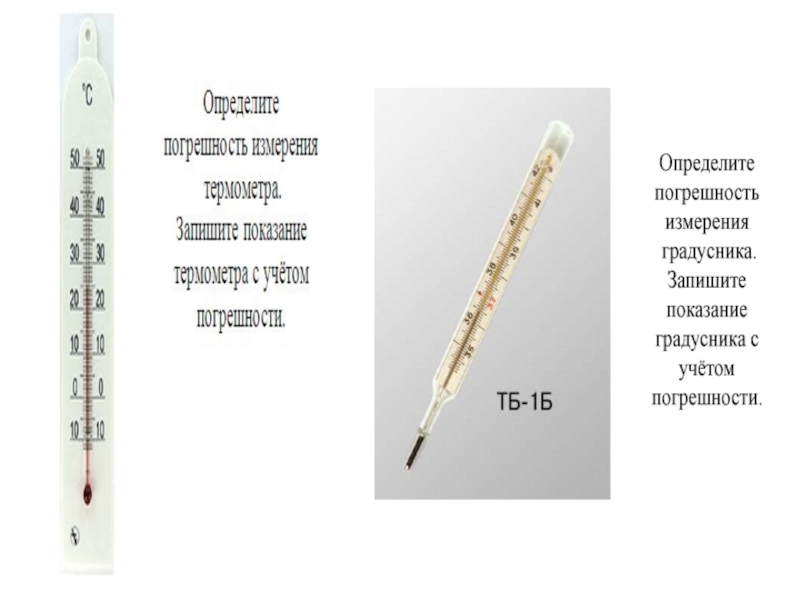
Погрешность и точность измерения.
какую-либо величину,
мы пользуемся специальными
измерительными приборами:
Слайд 12
Если а приближённое значение числа х и
Слайд 15Длины отрезка линейкой с миллиметровой шкалой
Промежутка времени часами с секундной стрелкой
Градусной
Какова точность измерения?
Слайд 18Какие из значений величин точные, какие приближенные:
Толщина книги 25 мм
Температура воздуха
В самолете 122 пассажира
Скорость звука в воздухе322м/с
Масса дыни 3,5 кг
Цена ручки 12 рублей
В тетради начерчен угол в 500
Рекорд соревнований в беге на 1500м равен 3 мин 56с
Слайд 21Относительная погрешность
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного
Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200 - 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.
Слайд 22
Пример В школе 1254 учащихся.
При округлении этого числа
При округлении до 1250: Δ = |1250 – 1254| = 4, а относительная погрешность или 0,3 %.
Слайд 23Задача. Продавец взвешивает арбуз на чашечных весах. В наборе гирь
Это число – приближенное. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г.
Относительная погрешность не превосходит
50/3600 ≈ 1,4%.
Ответ:
Слайд 24В большинстве случаев невозможно узнать точное значение приближенного числа, а значит,
Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая - 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза неизвестен. Но абсолютная погрешность не превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.
Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.
В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность - 1,4 %.
Слайд 27История создания
Разработка РСЗО «Град» началась еще в середине 50-х годов –
В итоге решили создать ракету со стабилизаторами, изогнутыми по цилиндрической поверхности. Это позволило использовать трубчатые направляющие и вписать реактивный снаряд в калибр 122 мм.