- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Наибольшее, наименьшее значение функции (11 класс)
Содержание
- 1. Презентация по математике на тему Наибольшее, наименьшее значение функции (11 класс)
- 2. (x²)′=(2x³)′=(7x)′=(10)′=(128 )′=(5x² + 3x - 9 )′=x²2x6x²00710x + 3
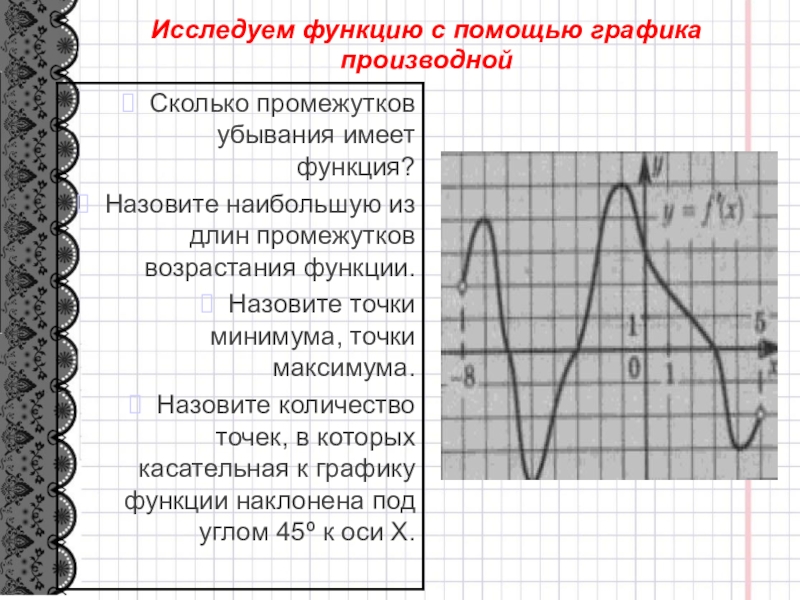
- 3. Исследуем функцию с помощью графика производной
- 4. Вопросы: 1. Область определения функции.2. Абсциссы точек,
- 5. Унаиб= f(b),b –конец отрезка Унаим=f(x1 ), x1
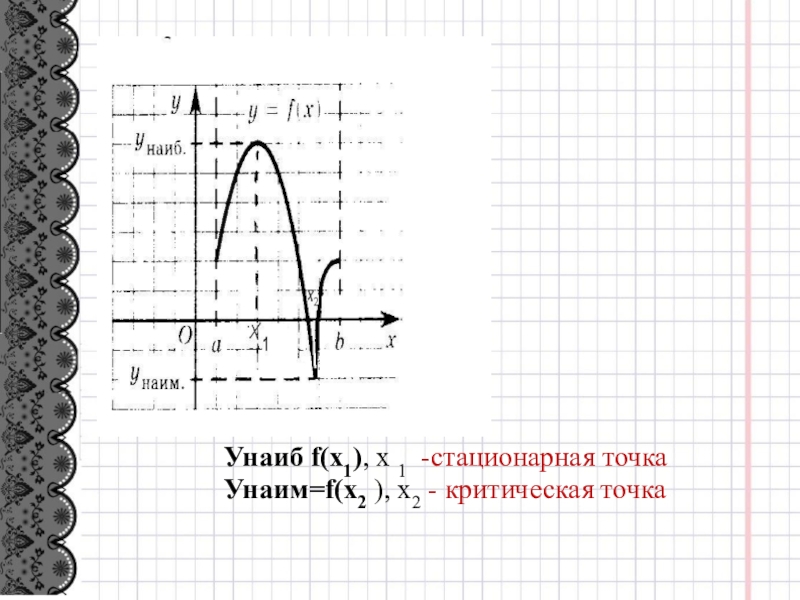
- 6. Унаиб f(x1), х 1 -стационарная точкаУнаим=f(x2 ), x2 - критическая точка
- 7. Нахождение наибольшего и наименьшего значения функции
- 8. АЛГОРИТМнайти критические точки функции на интервале (а; b);2.
- 9. Найдите наименьшее значение функции
- 10. Производная функции успешно применяется при решении оптимальных задач в различных сферах деятельности человека.
- 11. Задача. Из всех прямоугольников, периметр которых 32м,
- 12. Решение:Обозначим сторону прямоугольника аВторая сторона – (16-а)Площадь
- 13. Печатный текст (вместе с промежутками между строками)
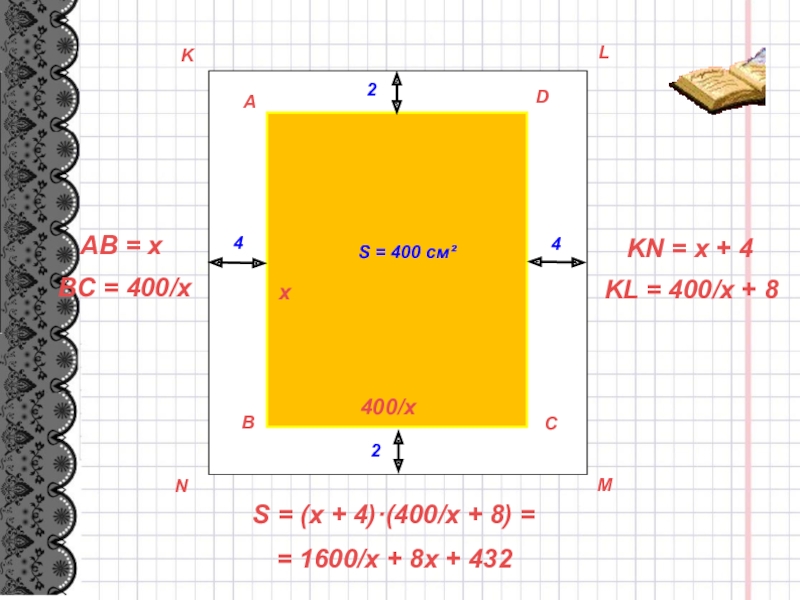
- 14. ABCDKLMN4422S = 400 см²х400/хAB = xBC =
- 15. S = 1600/x + 8x + 432
Слайд 4
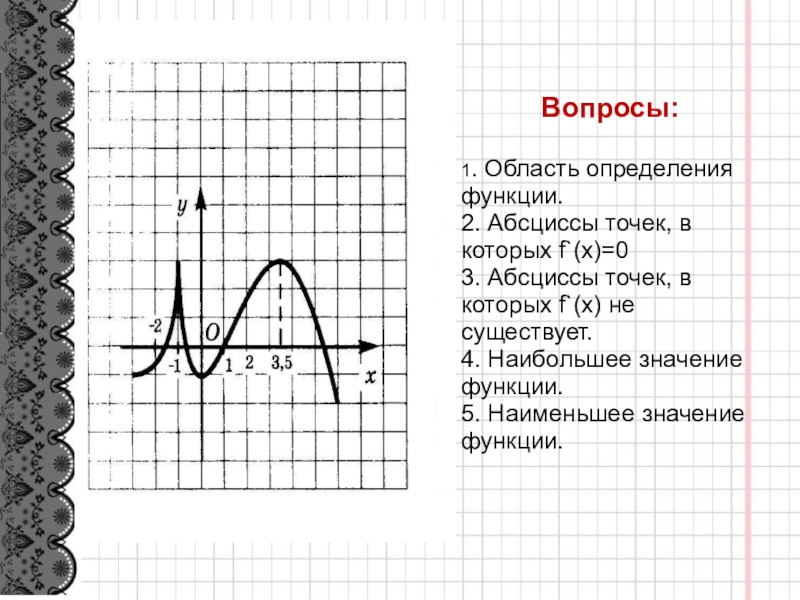
Вопросы:
1. Область определения функции.
2. Абсциссы точек, в которых f`(x)=0
3. Абсциссы точек, в которых f`(x) не существует.
4. Наибольшее значение функции.
5. Наименьшее значение функции.
Слайд 5
Унаиб= f(b),b –конец отрезка
Унаим=f(x1 ), x1 – стационарная точка, т.е.
Унаиб= f(а), а – конец отрезка
Унаим=f(b), b – конец отрезка.
Слайд 8АЛГОРИТМ
найти критические точки функции на интервале (а; b);
2. вычислить значения функции в
3. вычислить значения функции на концах отрезка, т. е. в точках х = а и х = b,
4. среди всех вычисленных значениях функции выбрать наибольшее и наименьшее.
Слайд 9 Найдите наименьшее значение функции
y = 3x2 –
Ответ: 1
Критических точек нет
Слайд 10Производная функции успешно применяется при решении оптимальных задач в различных сферах
Слайд 12Решение:
Обозначим сторону прямоугольника а
Вторая сторона – (16-а)
Площадь прямоугольника S= а(16-а)
Задача сводится
S(а) = а(16-а)
S’(а) = 16-2а
Функция S(а) определена при всех значениях переменной, кроме а>0. Решим уравнение S’(а) = 0, 16-2а = 0, а = 8
При а=8м наибольшая площадь составляет S(8) = 64м2
Слайд 13Печатный текст (вместе с промежутками между строками) одной страницы книги должен
Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?
Слайд 14
A
B
C
D
K
L
M
N
4
4
2
2
S = 400 см²
х
400/х
AB = x
BC = 400/x
KL = 400/x +
KN = x + 4
S = (x + 4)·(400/x + 8) =
= 1600/x + 8x + 432
Слайд 15S = 1600/x + 8x + 432 → min
1. S′ =
2. S′ = 0; -1600/x² + 8 = 0
1600/x² = 8
x² = 1600/8
x ≈ 14
3.
—
+
min
14
Оптимальные размеры страницы
18х36,5 см.
4. KN = х + 4=18
KL = 400/x + 8≈36,5

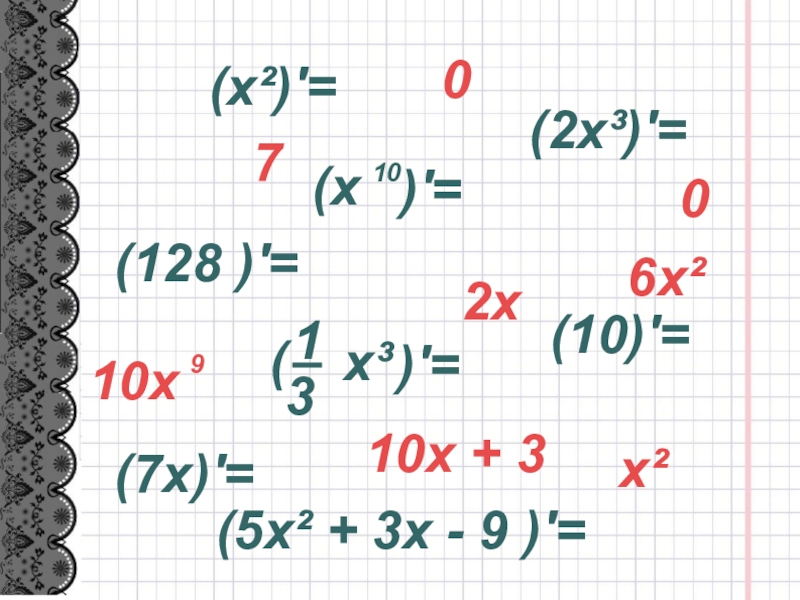



![Презентация по математике на тему Наибольшее, наименьшее значение функции (11 класс) Найдите наименьшее значение функции y = 3x2 – 2x3 Найдите наименьшее значение функции y = 3x2 – 2x3 + 1 на отрезке [-4;0]](/img/thumbs/847e70b4d6a1c8abe658fd16ef798f44-800x.jpg)