- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Методы решения тригонометрических уравнений
Содержание
- 1. Презентация по математике на тему Методы решения тригонометрических уравнений
- 2. Решение тригонометрических уравнений1. Простейшие уравнения2. Разложение на
- 3. Замена переменной –
- 4. Однородные тригонометрические уравнения Важно: справа 0,
- 5. a sin2x + bsinxcosx + c cos2x
- 6. Методы решения однородных тригонометрических уравнений Уравнения
- 7. Слайд 7
- 8. Слайд 8
- 9. 1234
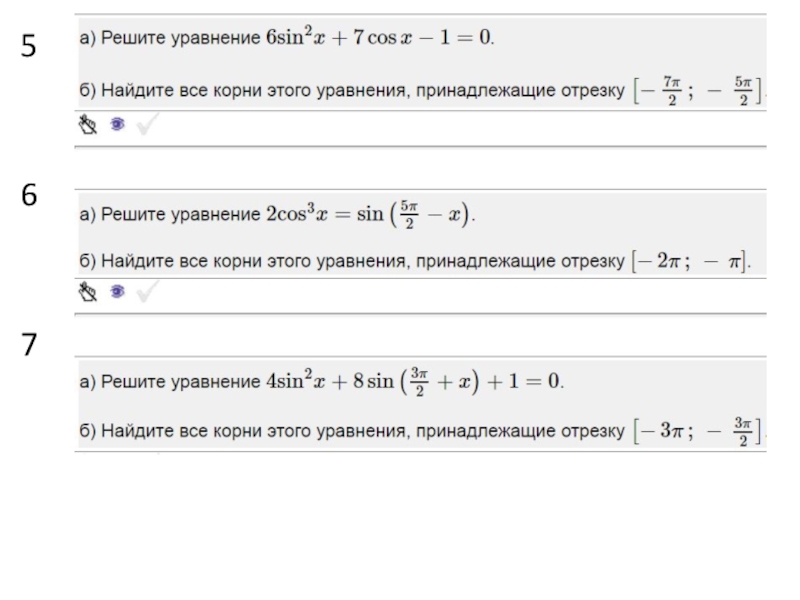
- 10. 567
- 11. 6.7.8.9.10.
- 12. Слайд 12
- 13. 1
- 14. Слайд 14
- 15. Слайд 15
Слайд 2Решение тригонометрических уравнений
1. Простейшие уравнения
2. Разложение на множители.
Разложить на множители
Слайд 3Замена переменной – Часто встречающиеся квадратные
Слайд 4Однородные тригонометрические уравнения
Важно: справа 0, а аргументы у функции
Перейти к тангенсу, так как «ко-функции» одного аргумента одновременно в 0 не обращаются.
asinx + bcosx = 0 (однородное уравнение первой степени) либо
a sin2x + bsinx·cosx + c cos2x = 0 (однородное уравнение второй степени).
Слайд 5a sin2x + bsinxcosx + c cos2x = 0 (однородное уравнение
sin2x – 10 sinx·cosx + 21cos2x = 0.
Т.к. cos2x ≠ 0, то tg2x – 10 tgx + 21 = 0
Замена:tgx = у.
у2 – 10 у + 21 = 0
у1 = 7 или у2 = 3
tgx = 7 или tgx = 3
tgx = 7:
х = arctg7 + πn, n ∈Z
tgx = 3:
х = arctg3 + πn, n ∈Z Ответ: arctg7 + πn, n ∈Z, arctg3 + πn, n ∈Z .
Слайд 6Методы решения однородных тригонометрических уравнений
Уравнения вида
аsinx + bcosx =
(однородное уравнение первой степени)
Важно: справа 0, а аргументы у функции и
«ко-функции» одинаковы.
Перейти к тангенсу, так как «ко-функции» одного аргумента
одновременно
в 0 не обращаются.
Уравнения вида
аsin2x + bsinx cosx + c cos2x = 0. (однородное уравнение второй степени).
Однородные тригонометрические уравнения второй степени решаются обычно делением обеих частей уравнения на cos2x (sin2x).
Квадратное однородное уравнение можно решать относительно одного из аргументов, считая другой «псевдопараметром».