- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: История открытия комплексных чисел
Содержание
- 1. Презентация по математике на тему: История открытия комплексных чисел
- 2. Понятие комплексных чиселКомплексное число — это выражение вида a + bi,
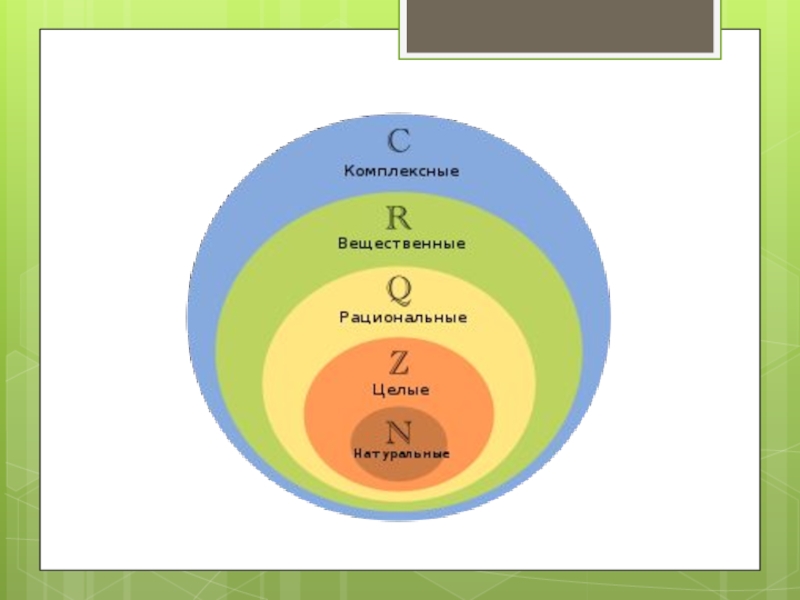
- 3. Слайд 3
- 4. Арифметические действия над комплексными числами те же,
- 5. История созданияИсторически комплексные числа впервые были введены
- 6. Хотя согласно некоторым источникам, по-видимому, мнимые величины
- 7. Продолжительное время стоял вопрос, является ли множество
- 8. Символ для обозначения мнимой единицы предложил швейцарский, немецкий
- 9. ~Спасибо за внимание~
Понятие комплексных чиселКомплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это
Слайд 2Понятие комплексных чисел
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i —
так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Слайд 4Арифметические действия над комплексными числами те же, что и над действительными:
их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число = a -bi называется комплексно- сопряженным к z = a + bi. Равенство z · = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число.
Слайд 5История создания
Исторически комплексные числа впервые были введены в связи с выведением
формулы вычисления корней кубического уравнения . Итальянский математик Никколо Фонтана Тартальей (1499 - 1557) в первой половине 16 века получил выражение для корня такого уравнения через некоторые параметры, для нахождения которых составляется система. Но было выяснено, что такая система не для всех кубических уравнений имела решение в действительных числах. Это непонятное на то время явление объяснил в 1572 году Рафаэль Бомбелли (1526 - 1572), что по сути было введением комплексных чисел и действий над ними. Но долгое время полученные результаты многими учеными считались сомнительными и лишь в 19 веке после появления трудов немецкого математика, механика, физика, астронома и геодезиста Карла Фридриха Гаусса (1777 - 1855) существование комплексных чисел стало общепризнанным.
Слайд 6Хотя согласно некоторым источникам, по-видимому, мнимые величины были впервые упомянуты в
1545 году в известном труде "Великое искусство, или об алгебраических правилах" итальянского математика, инженера, философа, медика и астролога Джероламо Кардано (1501 - 1576), в рамках формального решения задачи по вычислению двух чисел, которые в сумме дают 10, а при перемножении дают 40.
Слайд 7Продолжительное время стоял вопрос, является ли множество комплексных чисел замкнутым, то
есть все ли операции над комплексными числами являются приводят к комплексным или вещественным результатам, или, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней -ой степени из рассматриваемого комплексного числа была решена в работах английского математика Абрахама де Муавра (1667 - 1754) в 1707 году и английского математика и философа Роджера Котса (1682 - 1716) в 1722 году.
Слайд 8Символ для обозначения мнимой единицы предложил швейцарский, немецкий и российский математик и
механик Леонардо Эйлер в 1777, взявший для этого первую букву латинского слова "imaginarius" - мнимый. Он же распространил все стандартные функции, включая логарифм, на комплексную область.