- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии Прямоугольная система координат (11 класс)
Содержание
- 1. Презентация по геометрии Прямоугольная система координат (11 класс)
- 2. Исторические сведенияИстория возникновения координат и системы координат
- 3. Основная заслуга в создании современного метода координат
- 4. Научное описание прямоугольной системы координат Рене Декарт
- 5. Повторение:1. Даны точки А ( - 1;
- 6. Повторение:2. Запишите координаты вектора Ненулевые векторы наз.
- 7. Повторение:4. Найдите координаты вектора
- 8. Вопросы:1. Сколькими координатами может быть задана точка
- 9. Задание прямоугольной системы координат в пространстве:ОyОy
- 10. Нахождение координат точек. Точка лежитна осиОу (0;
- 11. Решение задач. Рассмотрим точку А (2; -3;
- 12. Решение задач. Рассмотрим точку А (2; -3;
- 13. Решение задач.хуzC1 - ?C - ?A1 (1;0;0)B1
Слайд 2Исторические сведения
История возникновения координат и системы координат начинается очень давно, первоначально
Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.
Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.
Слайд 3Основная заслуга в создании современного метода координат принадлежит французскому математику Рене
Слайд 4Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей
Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
Слайд 5Повторение:
1. Даны точки А ( - 1; 7 ) и В
а) Найдите координаты середины отрезка АВ.
С ( 3; 4)
б) Найдите длину отрезка АВ.
|АВ| = 10
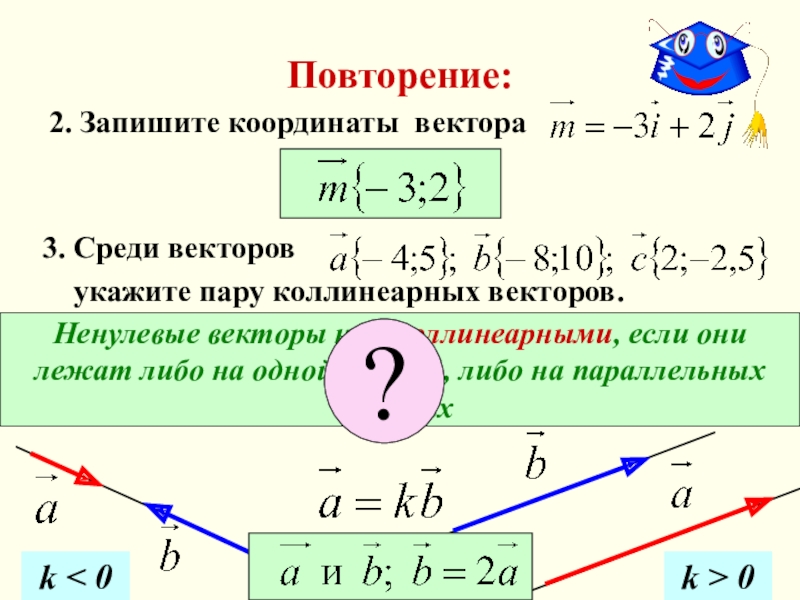
Слайд 6Повторение:
2. Запишите координаты вектора
Ненулевые векторы наз. коллинеарными, если они
лежат
прямых
3. Среди векторов
укажите пару коллинеарных векторов.
?
k < 0
k > 0
Слайд 7Повторение:
4. Найдите координаты вектора , если
5. Найдите расстояние между точками
А (а; 0) и В (b; 0).
Слайд 8Вопросы:
1. Сколькими координатами может быть задана точка на прямой?
Одной.
2. Сколькими
Двумя.
3. Сколькими координатами может быть задана точка в пространстве?
Вопрос урока.
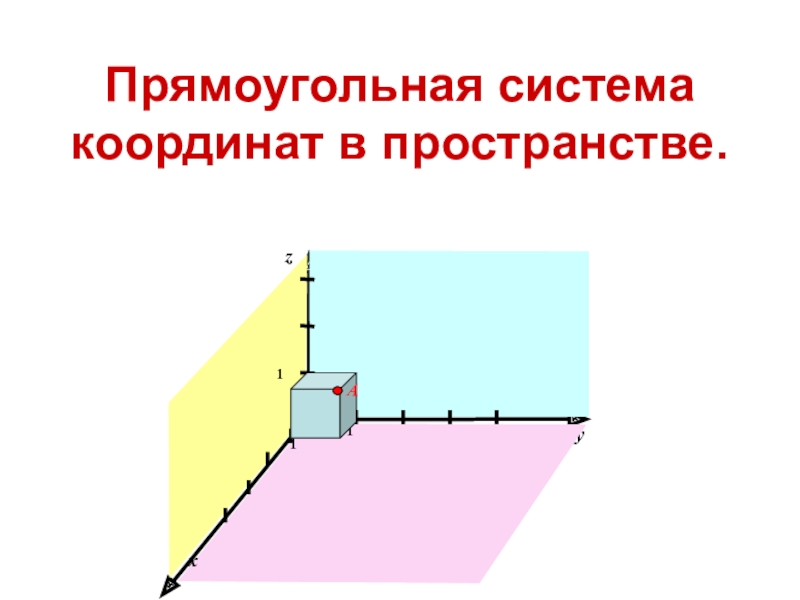
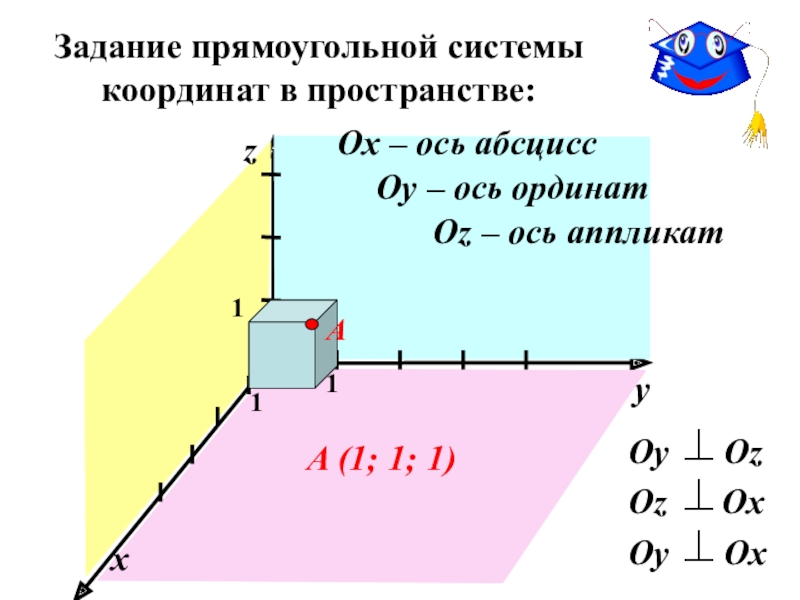
Слайд 9Задание прямоугольной системы
координат в пространстве:
О
y
Оy Оz
Оz
Оy Оx
x
z
1
1
1
A
A (1; 1; 1)
Ох – ось абсцисс
Оу – ось ординат
Оz – ось аппликат
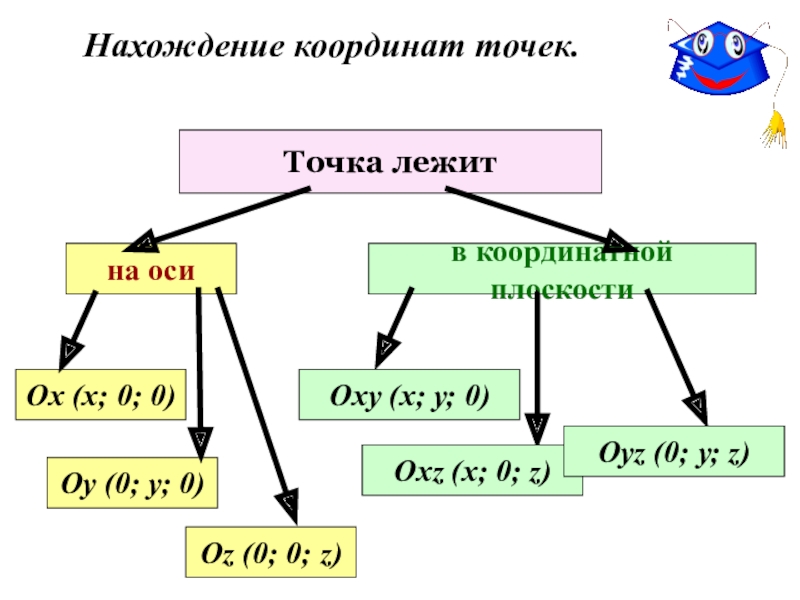
Слайд 10Нахождение координат точек.
Точка лежит
на оси
Оу (0; у; 0)
Ох (х; 0; 0)
Оz
в координатной плоскости
Оху (х; у; 0)
Охz (х; 0; z)
Оуz (0; у; z)
Слайд 11Решение задач.
Рассмотрим точку А (2; -3; 5)
х
у
z
0
2
5
-3
A
1) A1 : Oxy
A1
A1
A2
2) A2 : Oxz
A2 (2; 0; 5)
3) A3 : Oyz
A3
A3 (0; -3; 5)
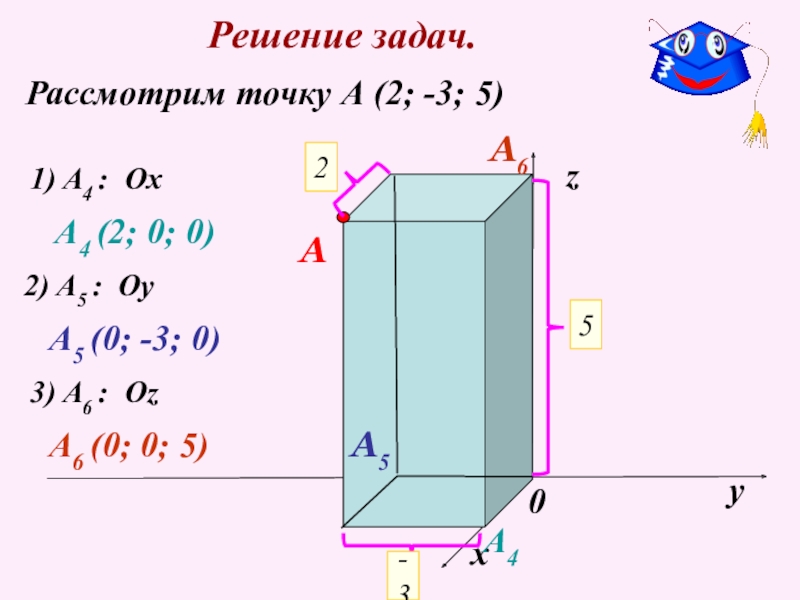
Слайд 12Решение задач.
Рассмотрим точку А (2; -3; 5)
х
у
z
0
2
5
-3
A
1) A4 : Ox
A4
A4
A5
2) A5 : Oу
A5 (0; -3; 0)
3) A6 : Oz
A6
A6 (0; 0; 5)
Слайд 13Решение задач.
х
у
z
C1 - ?
C - ?
A1 (1;0;0)
B1 - ?
D1 - ?
A
B (0;0;1)
D (0;1;0)
В1 (1; 0; 1)
С (0; 1; 0)
С1 (1; 1; 0)
D1 (1; 1; 1)