- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Текстовые задачи (11 класс)
Содержание
- 1. Презентация по алгебре на тему Текстовые задачи (11 класс)
- 2. Текстовые задачиПодготовила Птушкина Наталия Анатольевна, учитель математики МБОУ «Лицей №2» г. Чебоксары Чувашской Республики
- 3. На баржу было погружено 1215 т песка,
- 4. Слайд 4
- 5. B9. Магазин выставил на продажу товар
- 6. На рынке костюм, состоящий из пиджака и
- 7. Слайд 7
- 8. Пусть масса первого сплава
- 9. 1) В основании подставки лежит квадрат. Пусть
- 10. По пенсионному вкладу банк выплачивает 10%
- 11. Найдите двузначное число, если количество единиц в
Слайд 2Текстовые задачи
Подготовила Птушкина Наталия Анатольевна, учитель математики МБОУ «Лицей №2» г.
Слайд 3
На баржу было погружено 1215 т песка, влажность которого составляла 15%.
Неизменной при перевозке груза является сухая часть от перевозимого песка.
Было в пункте А: Стало в пункте В:
Ответ:1275
Слайд 4
Составим уравнение:
9(12-х)-9х=2х(12-х),
х2-21х+54=0,
х1=18
х1 не удовлетворяет смыслу задачи, так как скорость течения не может быть больше скорости лодки.
Значит, скорость плота 3 км/ч.
Ответ: 3
Каждая из двух пристаней находится от поселка на расстоянии 36 км (по реке).
От одной из них в сторону поселка отправился плот. Спустя 8 ч от другой
пристани навстречу плоту вышла лодка, собственная скорость которой 12 км/ч.
Найдите скорость плота, если в поселок плот и лодка прибыли одновременно.
плот
пристань
пристань
поселок
спустя
8 часов
36 км
36 км
12-х км/ч
х км/ч
х
12-х
36
36
Плот движется со скоростью течения
Слайд 5
B9. Магазин выставил на продажу товар с наценкой 50% от
Магазин получил прибыли 3∕8 х-7∕40 х=1∕5 х, значит, 20%.
Ответ: 0,2.
х
¾ х
х+0,5х=1,5х
¾*1,5х=9∕8х
9∕8х-¾х=3/8х
х
¼х=10/40х
1,5х-0,8*1,5х=0,3х
¼*0,3х=3∕40 х
10∕40х-3/40х=7/40х
Слайд 6
На рынке костюм, состоящий из пиджака и брюк, стоит на 20%
Составим уравнение:
0,8(х + у) = 0,9у+0,65х;
0,15х = 0,1у;
у=1,5х.
Стоимость пиджака составляет от стоимости костюма в магазине
Ответ: 60
у
х
х + у
у-0,1у=0,9у
х-0,35х=0,65х
0,9у+0,65х
на 20% дешевле
Слайд 7
х=320.
Значит, первый сотрудник должен был взять 320 страниц, отдав второму
560-х=560-320=240 страниц, то есть на 240 страниц меньше первоначального.
Ответ: 240
Двум сотрудникам издательства поручили отредактировать рукопись объемом 560 страниц. Один сотрудник, отдав второму 480 страниц рукописи, взял остальные страницы себе и выполнил свою часть работы за время, в 8 раз меньшее, чем второй – свою. На сколько страниц меньше первый сотрудник должен был отдать второму (добавив их себе), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?
560-480=80
480
t
8t
х
560-х
Пусть х страниц рукописи первый сотрудник должен был взять себе.
Учитывая, что работа должна быть выполнена за одинаковое время, составим уравнение:
Слайд 8
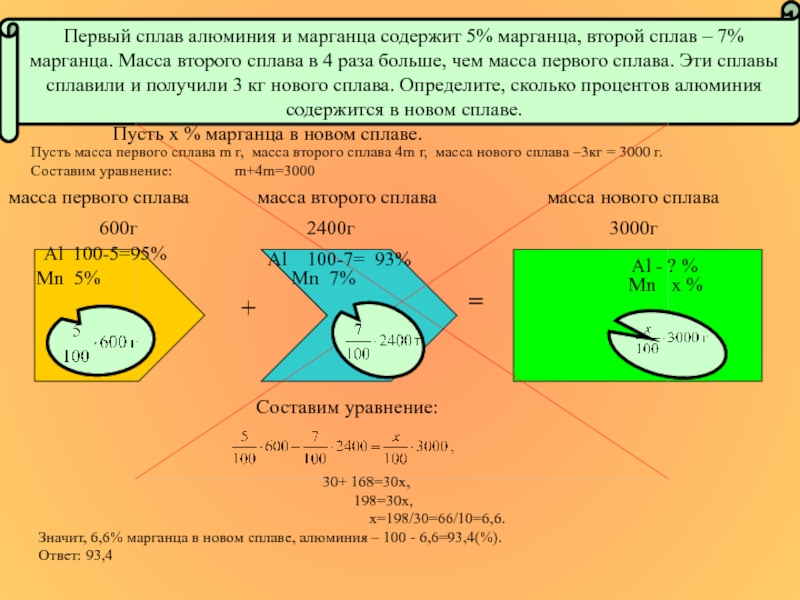
Пусть масса первого сплава m г, масса второго
Составим уравнение: m+4m=3000
30+ 168=30х,
198=30х,
х=198/30=66/10=6,6.
Значит, 6,6% марганца в новом сплаве, алюминия – 100 - 6,6=93,4(%).
Ответ: 93,4
Первый сплав алюминия и марганца содержит 5% марганца, второй сплав – 7% марганца. Масса второго сплава в 4 раза больше, чем масса первого сплава. Эти сплавы сплавили и получили 3 кг нового сплава. Определите, сколько процентов алюминия содержится в новом сплаве.
=
+
600г
2400г
3000г
масса первого сплава
масса второго сплава
масса нового сплава
Al
Mn 5%
Al
Mn 7%
Al - ? %
Mn х %
Пусть х % марганца в новом сплаве.
Составим уравнение:
100-5=95%
100-7= 93%
Слайд 91) В основании подставки лежит квадрат. Пусть длина его стороны -
Тогда ее объем равен ах2 , и составляет 1296 дм3, выразим длину ребра а: .
2) Сварить надо 3 ребра верхнего основания и 2 ребра грани, параллельной стороне. Общая длина
сварочного шва: L=3х+2а=3х+ . Рассмотрим ее как функцию от х и выясним, при
каком значении х функция у = L(х) достигает своего наименьшего значения на промежутке (0;+∞).
3) Найдем производную .
Поэтому ,т.е. функция L(х) при х >0 имеет единственную критическую точку х=12.
4)
Значит, х=12 является точкой минимума и при х =12 функция у = L(х) достигает своего н наименьшего значения.
Тогда высота подставки равна
Поэтому необходима подставка, длина квадратного основания которой 12 дм, высота о подставки равна 9 дм.
Ответ:12дм, 12дм, 9дм.
Для монтажа оборудования необходима подставка объемом 1296 дм3 в форме прямоугольного
параллелепипеда. Квадратное основание подставки будет вмонтировано в пол, а ее задняя стенка –
в стену цеха. Для соединения подставки по ребрам, не вмонтированным в пол или стену,
используется сварка. Определите размеры подставки, при которых общая длина сварочного шва
будет наименьшей.
Слайд 10
По пенсионному вкладу банк выплачивает 10% годовых. По истечении каждого
проценты капитализируются, т.е.начисленная сумма присоединяется к вкладу. На данный
вид вклада был открыт счет в 50 000 рублей, который не пополнялся и с которого не
снимали деньги в течение 3 лет. Какой доход был получен по истечении этого срока?
Было 50000 рублей, 10%=10/100=0,1.
В конце 1 года
50000+0,1*50000=1,1*50000=55000
В конце 2 года
55000+0,1*55000=1,1*55000=60500
В конце 3 года
60500+0,1*60500=1,1*60500=66550
Ответ: 66550.
или по формуле
рублей, где а –сумма вклада, n –количество лет.
Используя формулу, получим:
Слайд 11
Найдите двузначное число, если количество единиц в нем на 4 больше
ху=10х+у – искомое двузначное число.
Пусть х – количество десятков (1< х<9), у – количество единиц (0<у<9).
Зная, что количество единиц на 4 больше количества десятков,
составим уравнение: у-х=4.
Произведение искомого числа на сумму его цифр равно 90.
Составим второе уравнение: (10х + у)(х + у)=90.
Составим и решим систему уравнений: у-х=4,
(10х + у)(х + у)=90;
у=4+х, у=5,
(10х+4+х)(х+4+х)=90; х1=1,
х2<0 не удовлетворяет условию 1<х<9;
Значит, двузначное число содержит 1 десяток 5 единиц, искомое число 15.
Ответ: 15