- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Подготовка к ЕГЭ. Решение задач по теории вероятностей.
Содержание
- 1. Презентация по математике Подготовка к ЕГЭ. Решение задач по теории вероятностей.
- 2. Справочный материалЭлементарные события (исходы) – простейшие события,
- 3. Вероятности противоположных событий:Формула сложения вероятностей:Формула сложения для
- 4. Задачи по теме:« Определение вероятности»
- 5. Схема решения задач:Определить, в чем состоит случайный
- 6. Задача 1. Вася, Петя, Коля и Леша
- 7. Реши самостоятельно!Дежурные по классу Алексей, Иван, Татьяна
- 8. Задание 4 № 1001. На экзамен вынесено 60 вопросов,
- 9. Задание 4 № 1024. На тарелке 16 пирожков: 7
- 10. Задание 4 № 282856. В среднем из 1000 садовых
- 11. Задание 4 № 282858. В соревнованиях по толканию ядра
- 12. Реши самостоятельно!Какова вероятность того, что случайно выбранное
- 13. На клавиатуре телефона 10 цифр, от 0
- 14. Задача 2. Игральный кубик бросили один раз.
- 15. Реши самостоятельно!В случайном эксперименте игральный кубик бросают
- 16. Реши самостоятельно!В случайном эксперименте игральный кубик бросают
- 17. Реши самостоятельно!В случайном эксперименте игральный кубик бросают
- 18. Реши самостоятельно!Игральный кубик бросают дважды. Найдите вероятность
- 19. Задача 4. В случайном эксперименте бросают два
- 20. Реши самостоятельно!Игральный кубик бросают дважды. Найдите вероятность
- 21. Реши самостоятельно!Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна?Ответ: 7
- 22. В случайном эксперименте бросают две игральные кости.
- 23. Задача 3. В случайном эксперименте симметричную монету
- 24. Реши самостоятельно!Монету бросают дважды. Найдите вероятность того, что выпадет хотя бы один ОРЕЛ.Ответ: 0,75
- 25. Реши самостоятельно!В случайном эксперименте симметричную монету бросают
- 26. Решение:ООООООРРРРРРРРРРРРООООООМножество элементарных исходов:N=8A= {орел выпал ровно 2
- 27. Монету бросают три раза. Какова вероятность того, что результаты двух первых бросков будут одинаковы?Реши самостоятельно!Ответ: 0,5
- 28. Монету бросают три раза. Найдите вероятность того, что результаты первого и последнего броска различны.Реши самостоятельно!Ответ: 0,5
- 29. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.Реши самостоятельно!Ответ: 0,25
- 30. Реши самостоятельно!Перед началом футбольного матча судья бросает
- 31. Задача 6. В соревнованиях по толканию ядра
- 32. Решение:N= 1000A= {аккумулятор исправен}N(A)= 1000 – 6
- 33. Задача 8. В чемпионате по гимнастике участвуют
- 34. Задача 9. В чемпионате мира участвуют 16
- 35. В группе туристов 24 человека. С помощью
- 36. В некотором городе из 5000 появившихся на
- 37. На семинар приехали 3 ученых из Норвегии,
- 38. Научная конференция проводится в 5 дней. Всего
- 39. Задача 10. Вероятность того, что шариковая ручка
- 40. Задача 11. На экзамене по геометрии школьнику
- 41. Ковбой Джон попадает в муху на стене
- 42. А={кофе закончится в первом автомате}B={кофе закончится во
- 43. Задача 13. Биатлонист пять раз стреляет по
- 44. Задача 14. В магазине стоят два платежных
- 45. Если гроссмейстер А. играет белыми, то он
- 46. . Вероятность того, что батарейка бракованная, равна
Слайд 2Справочный материал
Элементарные события (исходы) – простейшие события, которыми может окончится случайный
Сумма вероятностей всех элементарных событий равна 1.
Р(А) равна сумме вероятностей элементарных событий, благоприятствующих этому событию.
(объединение) – событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий А,В
(пересечение) – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям А и В.
называется противоположным событию А, если состоит из тех и только тех элементарных исходов, которые не входят в А.
Несовместные события – это события, которые не наступают в одном опыте.
Слайд 3Вероятности противоположных событий:
Формула сложения вероятностей:
Формула сложения для несовместных событий:
Формула умножения вероятностей:
Условная
Формула вероятности k успехов в серии из n испытаний Бернулли:
р – вероятность успеха, q=1-p вероятность неудачи в одном испытании
Слайд 5Схема решения задач:
Определить, в чем состоит случайный эксперимент и какие у
Найти общее число элементарных событий (N)
Определить, какие элементарные события благоприятствуют событию А, и найти их число N(A).
Найти вероятность события А по формуле
Слайд 6Задача 1. Вася, Петя, Коля и Леша бросили жребий – кому
Решение:
Случайный эксперимент – бросание жребия.
Элементарное событие – участник, который выиграл жребий.
Число элементарных событий: N=4
Событие А = {жребий выиграл Петя}, N(A)=1
Ответ: 0,25
Слайд 7Реши самостоятельно!
Дежурные по классу Алексей, Иван, Татьяна и Ольга бросают жребий
Алексей
Иван
Татьяна
Ольга
Ответ: 0,5
Слайд 8Задание 4 № 1001. На экзамен вынесено 60 вопросов, Андрей не выучил 3
Задание 4 № 1011. В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Слайд 9Задание 4 № 1024. На тарелке 16 пирожков: 7 с рыбой, 5 с
Задание 4 № 282855. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Слайд 10Задание 4 № 282856. В среднем из 1000 садовых
насосов, поступивших в продажу,
Найдите вероятность того, что один случайно
выбранный для контроля насос не
подтекает.
Здание 4 № 282857. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
0,93
Слайд 11Задание 4 № 282858. В соревнованиях по толканию ядра участвуют 4 спортсмена из
Задание 4 № 283479.
В чемпионате по гимнастике участвуют 50 спортсменок: 24 из США, 13 из Мексики, остальные — из Канады. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Канады.
Слайд 12Реши самостоятельно!
Какова вероятность того, что случайно выбранное натуральное число от 10
10, 11, 12, 13, 14, 15, 16, 17, 18, 19
Ответ: 0,3
Слайд 13
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность
Какова вероятность того, что случайно выбранное натуральное число от 58 до 82 делится на 6?
Решение.
На клавиатуре телефона 10 цифр, из них 5 нечетных: 1, 3, 5, 7, 9. Поэтому вероятность того, что случайно будет нажата нечетная цифра равна 5 : 10 = 0,5.
Решение.
Натуральных чисел от 58 до 82 - 25 чисел, из них на 6 делятся 4 числа: 60, 66, 72, 78. Следовательно, искомая вероятность равна
Слайд 14Задача 2. Игральный кубик бросили один раз. Какова вероятность того, что
Решение:
Случайный эксперимент – бросание кубика.
Элементарное событие – число на выпавшей грани.
Ответ:1/3
Всего граней:
1, 2, 3, 4, 5, 6
Элементарные события:
N=6
N(A)=2
Слайд 15Реши самостоятельно!
В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность
Ответ: 0,5
1, 2, 3, 4, 5, 6
Слайд 16Реши самостоятельно!
В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность
Ответ: 0,5
1, 2, 3, 4, 5, 6
Слайд 17Реши самостоятельно!
В случайном эксперименте игральный кубик бросают один раз. Найдите вероятность
Ответ: 1/3
1, 2, 3, 4, 5, 6
Слайд 18Реши самостоятельно!
Игральный кубик бросают дважды. Найдите вероятность того, что первый раз
Ответ: 1/6
Всего вариантов 36
Комбинаций с первой «6»
61,62,63,64,65,66
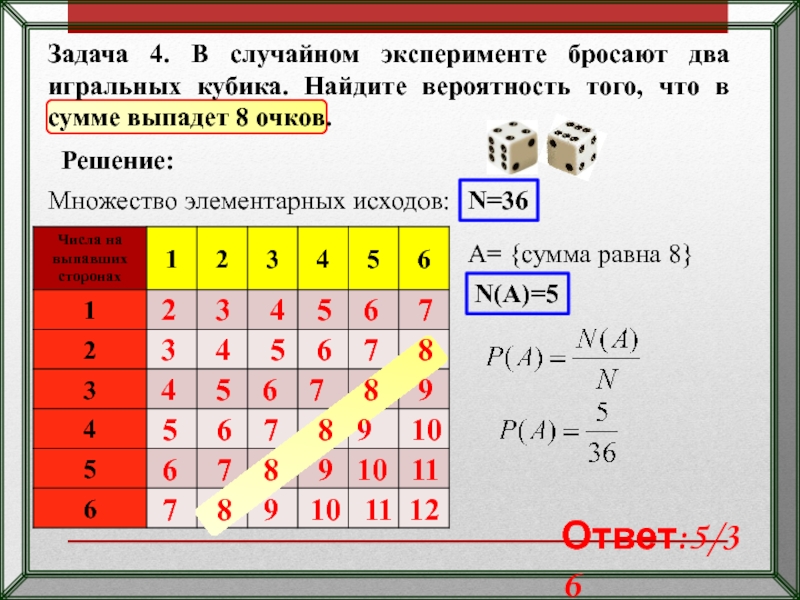
Слайд 19Задача 4. В случайном эксперименте бросают два игральных кубика. Найдите вероятность
Множество элементарных исходов:
Решение:
2 3 4 5 6 7
3 4 5 6 7 8
4 5 6 7 8 9
5 6 7 8 9 10
6 7 8 9 10 11
7 8 9 10 11 12
N=36
A= {сумма равна 8}
N(А)=5
Ответ:5/36
Слайд 20Реши самостоятельно!
Игральный кубик бросают дважды. Найдите вероятность того, что первый раз
Ответ: 1/6
Слайд 21Реши самостоятельно!
Игральный кубик бросают дважды. Какая сумма очков наиболее вероятна?
Ответ: 7
Слайд 22В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что
Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Решение:
Сумма очков может быть равна 5 в четырех случаях: «3 + 2», «2 + 3», «1 + 4», «4 + 1».
Ответ: 4.
Слайд 23Задача 3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность
Решение:
орел - О
решка - Р
Возможные исходы события:
О
Р
О
О
О
Р
Р
Р
N=4
N(A)=2
Ответ:0,5
4 исхода
Слайд 24Реши самостоятельно!
Монету бросают дважды. Найдите вероятность того, что выпадет хотя бы
Ответ: 0,75
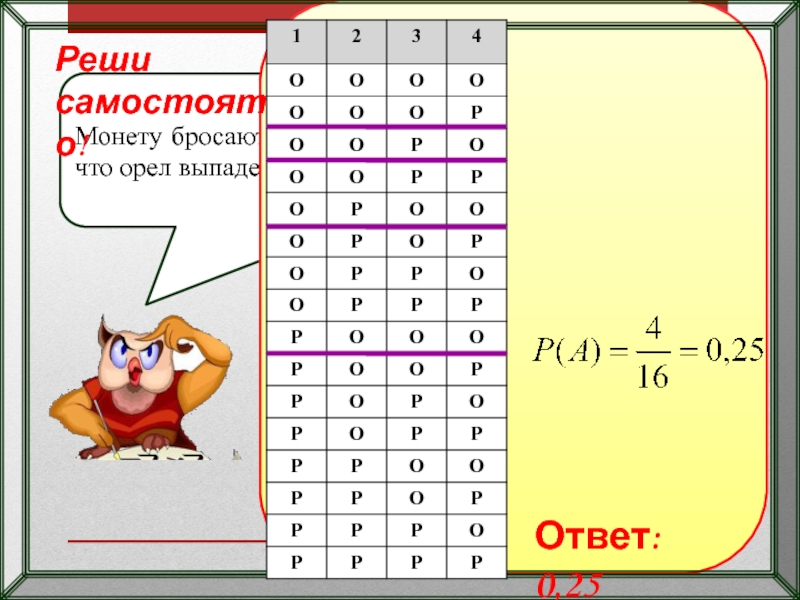
Слайд 25Реши самостоятельно!
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того,
Ответ: 0,25
Слайд 26Решение:
О
О
О
О
О
О
Р
Р
Р
Р
Р
Р
Р
Р
Р
Р
Р
Р
О
О
О
О
О
О
Множество элементарных исходов:
N=8
A= {орел выпал ровно 2 }
N(А)=3
Ответ: 0,375
8 исходов
Задача 5.
Слайд 27Монету бросают три раза. Какова вероятность того, что результаты двух первых
Реши самостоятельно!
Ответ: 0,5
Слайд 28Монету бросают три раза. Найдите вероятность того, что результаты первого и
Реши самостоятельно!
Ответ: 0,5
Слайд 29Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно
Реши самостоятельно!
Ответ: 0,25
Слайд 30Реши самостоятельно!
Перед началом футбольного матча судья бросает монету, чтобы определить, какая
Решение.
Обозначим «1» ту сторону монеты,
которая отвечает за выигрыш жребия
«Физиком», другую сторону монеты
обозначим «0». Тогда благоприятных
комбинаций три: 110, 101, 011, а всего
комбинаций 8: 000, 001, 010, 011, 1
00, 101, 110, 111. Тем самым, искомая вероятность равна:
Слайд 31Задача 6. В соревнованиях по толканию ядра участвуют 4 спортсмена из
Решение:
Всего спортсменов: N= 4 + 7 + 9 + 5 = 25
A= {последний из Швеции}
N=25
N(А)=9
Ответ: 0,36
Слайд 32Решение:
N= 1000
A= {аккумулятор исправен}
N(A)= 1000 – 6 = 994
Ответ: 0,994
Задача 7.
Слайд 33Задача 8. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из
Решение:
Определите N
Определите N(A)
Реши самостоятельно
Проверка:
N = 20
N(A)= 20 – 8 – 7 = 5
Ответ: 0,25
A= {первой будет спортсменка из Китая}
Слайд 34Задача 9. В чемпионате мира участвуют 16 команд. С помощью жребия
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе.
Решение:
Множество элементарных событий: N=16
A={команда России во второй группе}
С номером «2» четыре карточки: N(A)=4
Ответ: 0,25
Слайд 35В группе туристов 24 человека. С помощью жребия они выбирают трех
Реши самостоятельно!
Ответ: 0,125
Слайд 36В некотором городе из 5000 появившихся на свет младенцев оказалось 2512
Реши самостоятельно!
Ответ: 0,498
5000 – 2512 = 2488
Слайд 37На семинар приехали 3 ученых из Норвегии, 3 из России и
Решение.
Всего в семинаре принимает участие 3 + 3 + 4 = 10 ученых, значит, вероятность того, что ученый, который выступает восьмым, окажется из России, равна 3:10 = 0,3.
Ответ: 0,3.
Слайд 38Научная конференция проводится в 5 дней. Всего запланировано 75 докладов —
Решение.
За первые три дня будет прочитан 51 доклад, на последние два дня планируется 24 доклада. Поэтому на последний день запланировано 12 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна
Ответ: 0,16.
Слайд 39Задача 10. Вероятность того, что шариковая ручка пишет плохо (или не
Решение:
A={ручка пишет хорошо}
Противоположное событие:
Ответ: 0,9
Слайд 40Задача 11. На экзамене по геометрии школьнику достается один вопрос из
Решение:
А={вопрос на тему «Вписанная окружность»}
B={вопрос на тему «Параллелограмм»}
События А и В несовместны, т.к. нет вопросов относящихся к двум темам одновременно
С={вопрос по одной из этих тем}
Р(С)=Р(А) + Р(В)
Р(С)=0,2 + 0,15=0,35
Ответ: 0,35
Слайд 41Ковбой Джон попадает в муху на стене с вероятностью 0,8, если
Решение.
Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0,2·(1 − 0,8) = 0,04 и 0,8·(1 − 0,2) = 0,64. Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий: 0,04 + 0,64 = 0,68.
Ответ: 0,68.
Слайд 42А={кофе закончится в первом автомате}
B={кофе закончится во втором автомате}
Р(А)=Р(В)=0,3
По формуле сложения
Ответ: 0,52
Решение:
Задача 12. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Слайд 43Задача 13. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в
Решение:
Вероятность попадания = 0,8
Вероятность промаха = 1 - 0,8 = 0,2
А={попал, попал, попал, промахнулся, промахнулся}
По формуле умножения вероятностей
Р(А)= 0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2
Р(А)= 0,512 ∙ 0,04 = 0,02048 ≈ 0,02
Ответ: 0,02
Слайд 44Задача 14. В магазине стоят два платежных автомата. Каждый из них
Решение:
По формуле умножения вероятностей:
А={хотя бы один автомат исправен}
Ответ: 0,9975
Слайд 45Если гроссмейстер А. играет белыми, то он выигрывает
у гроссмейстера Б.
черными, то А. выигрывает у Б. с вероятностью 0,34.
Гроссмейстеры А. и Б. играют две партии, причем во
второй партии меняют цвет фигур. Найдите вероятность того,
что А. выиграет оба раза.
Решение.
Возможность выиграть первую и вторую партию не
зависят друг от друга. Вероятность произведения
независимых событий равна произведению их
вероятностей: 0,5 · 0,34 = 0,17.
Ответ: 0,17
Слайд 46. Вероятность того, что батарейка бракованная,
равна 0,06. Покупатель в магазине
случайную упаковку, в которой две таких батарейки.
Найдите вероятность того, что обе батарейки окажутся
исправными
Решение.
Вероятность того, что батарейка исправна,
равна 0,94. Вероятность произведения
независимых событий (обе батарейки
окажутся исправными) равна произведению
вероятностей этих событий: 0,94·0,94 = 0,8836.
Ответ: 0,8836