- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Решение квадратных неравенств (9 класс)
Содержание
- 1. Презентация по алгебре на тему Решение квадратных неравенств (9 класс)
- 2. Квадратные неравенства.Квадратные неравенства.Ребята, мы уже умеем решать
- 3. Квадратные неравенства.Решить неравенство:Решение:Найдем корни уравнения Построим график
- 4. Квадратные неравенства.2. Решить неравенство:Решение:Преобразуем неравенство: Разделим неравенство на
- 5. Квадратные неравенства.3. Решить неравенство:Решение: Найдем корни нашего трехчлена,
- 6. Квадратные неравенства.4. Решить неравенство:Решение: Найдем корни трехчлена и
- 7. Квадратные неравенства.Задачи для самостоятельного решения.Решить неравенство: a)b) c) d)
Слайд 2Квадратные неравенства.
Квадратные неравенства.
Ребята, мы уже умеем решать квадратные уравнения. Теперь давайте
Квадратным неравенством называется неравенство вот такого вида: . Знак неравенства может стоять любой, коэффициенты а, b, c – любые числа (а≠0).
Все правила, которые мы определили для линейных неравенств работают и тут. Эти правила повторите самостоятельно!
Введем еще одно важное правило:
Если у трехчлена отрицательный дискриминант, то если подставить любое значение х, знак трехчлена будет такой же как и знак у коэффициента а.
Квадратные неравенства можно решать строя графики или путем построения интервалов, давайте посмотрим примеры решений неравенств.
Слайд 3Квадратные неравенства.
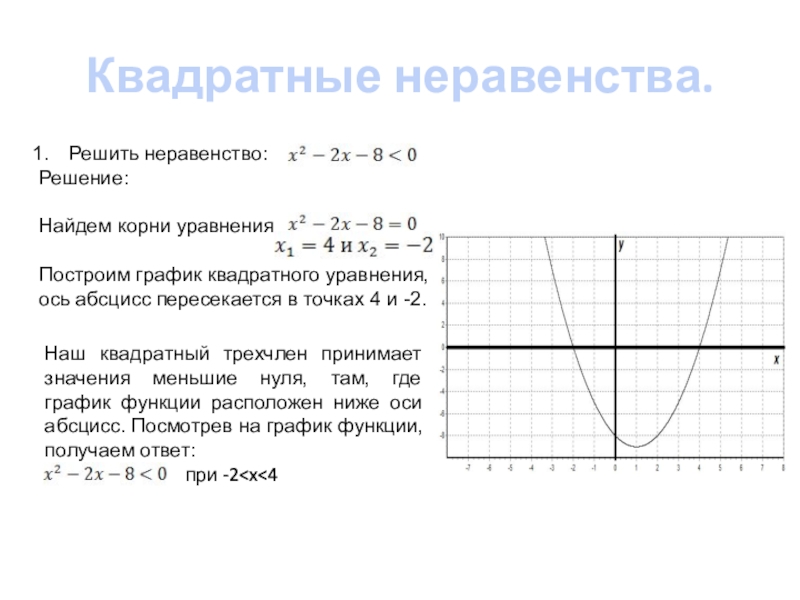
Решить неравенство:
Решение:
Найдем корни уравнения
Построим график квадратного уравнения,
ось абсцисс
Наш квадратный трехчлен принимает значения меньшие нуля, там, где график функции расположен ниже оси абсцисс. Посмотрев на график функции, получаем ответ:
при -2
Слайд 4Квадратные неравенства.
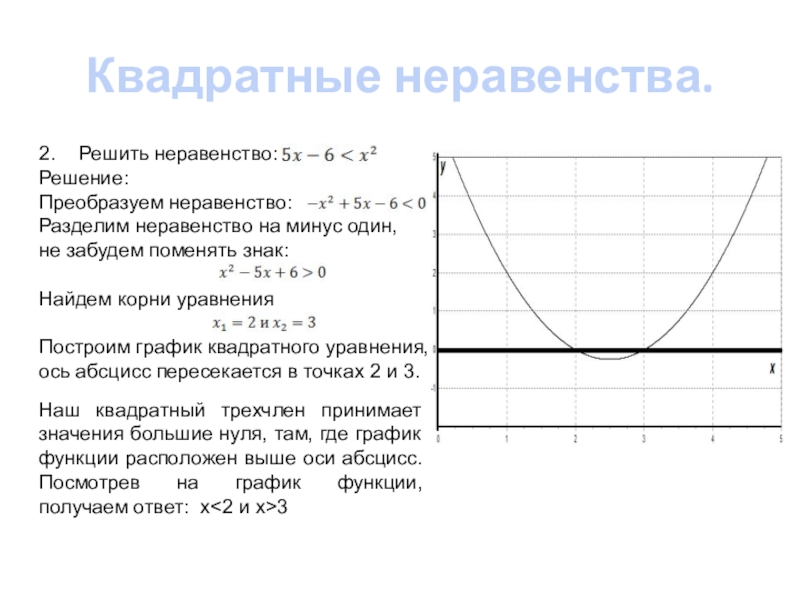
2. Решить неравенство:
Решение:
Преобразуем неравенство:
Разделим неравенство на минус один,
не забудем
Найдем корни уравнения
Построим график квадратного уравнения,
ось абсцисс пересекается в точках 2 и 3.
Наш квадратный трехчлен принимает значения большие нуля, там, где график функции расположен выше оси абсцисс. Посмотрев на график функции, получаем ответ: x<2 и x>3
Слайд 5Квадратные неравенства.
3. Решить неравенство:
Решение:
Найдем корни нашего трехчлена, для этого вычислим дискриминант:
Дискриминант
Ответ: При всех х, неравенство больше нуля.
Слайд 6Квадратные неравенства.
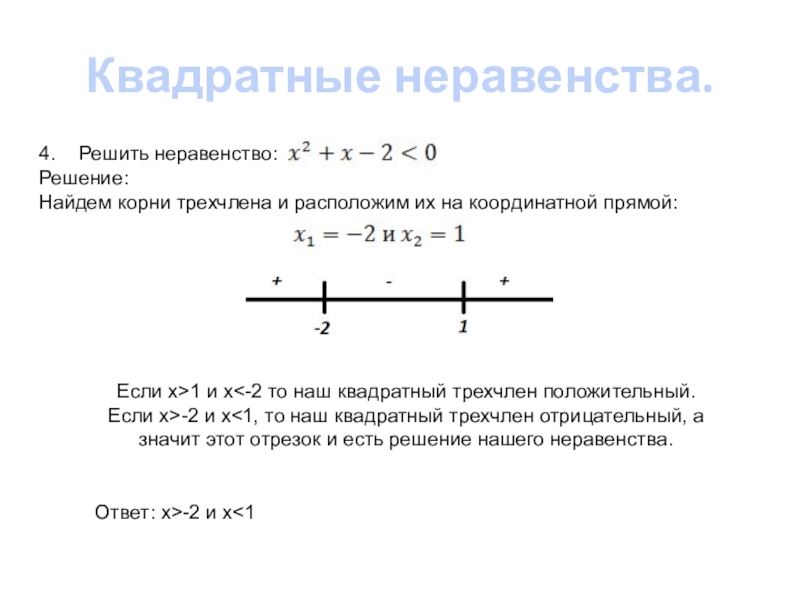
4. Решить неравенство:
Решение:
Найдем корни трехчлена и расположим их на координатной
Если x>1 и x<-2 то наш квадратный трехчлен положительный.
Если x>-2 и x<1, то наш квадратный трехчлен отрицательный, а значит этот отрезок и есть решение нашего неравенства.
Ответ: x>-2 и x<1