- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по алгебре на тему Производная и ее применение (11 класс)
Содержание
- 1. Презентация по алгебре на тему Производная и ее применение (11 класс)
- 2. Основоположники дифференциального исчисления И. Ньютон Г.Лейбниц
- 3. Понятие производной вошло в математику почти одновременно
- 4. Цель урока: систематизировать и обобщить знания учащихся;
- 5. ИГРА «БРЕЙН-РИНГ»1-й тур 1.Разминка
- 6. Вопросы1.Сформулируйте определение производной функции в точке.2.В чем
- 7. 1. Определение
- 8. k – угловой
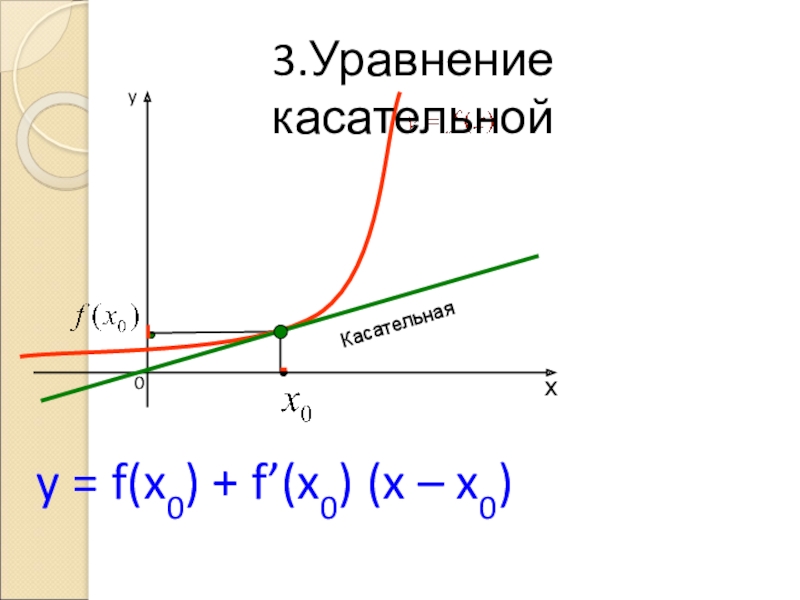
- 9. Касательнаяy = f(x0) + f’(x0) (x – x0) 3.Уравнение касательной
- 10. .Δх – перемещение телаΔt – промежуток временив течение которого выполнялосьдвижение4.Физический смысл производной
- 11. 5.Правила дифференцированияПроизводная суммы(разности)(u+v)'=u'+v' (u-v)'=u'-v'Производная произведения(uv)'=u'v+ uv' Производная частного (Сu)’=Cu’
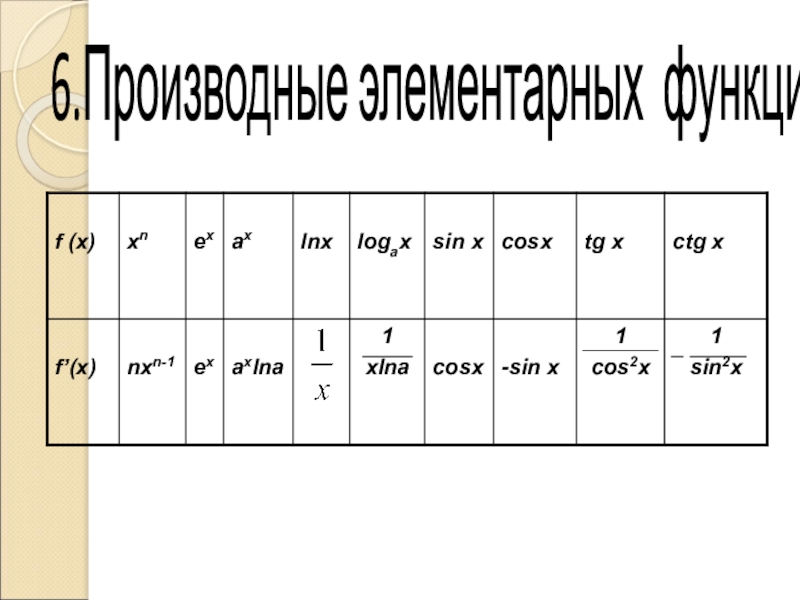
- 12. 6.Производные элементарных функций
- 13. Функция возрастает на некотором промежутке, если f’(x)>0
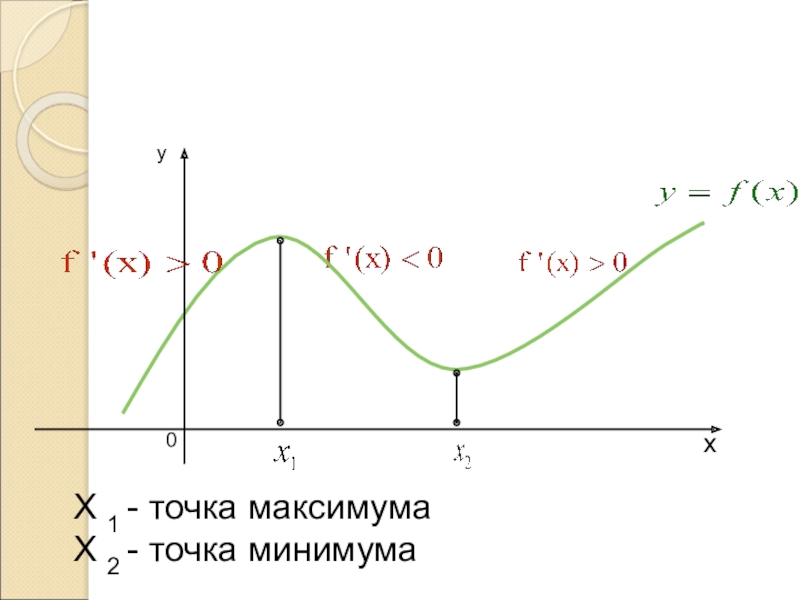
- 14. 8.Экстремумы функцииX 1 - точка максимума X 2 - точка минимума
- 15. 9.Наибольшее и наименьшее значение функции на
- 16. 10.Схема исследования функции и построения графика1.Найти область
- 17. 2.Найди производную.Вариант-11. у = х42. у =
- 18. 2-й тур 1.В таблице перепутан порядок записи
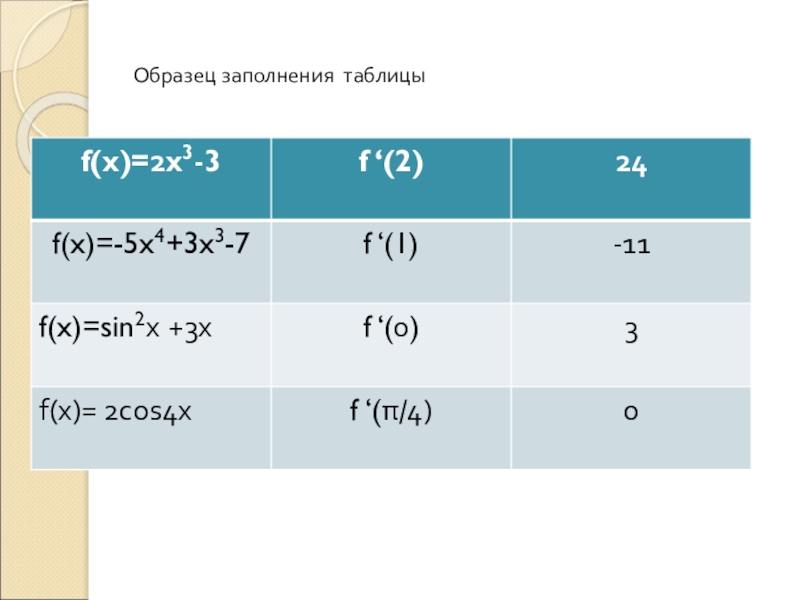
- 19. Образец заполнения таблицы
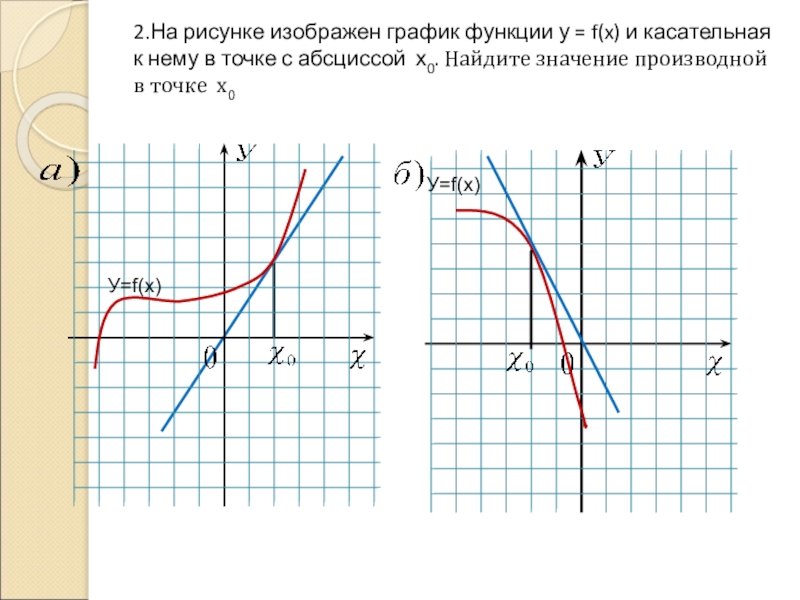
- 20. 2.На рисунке изображен график функции у
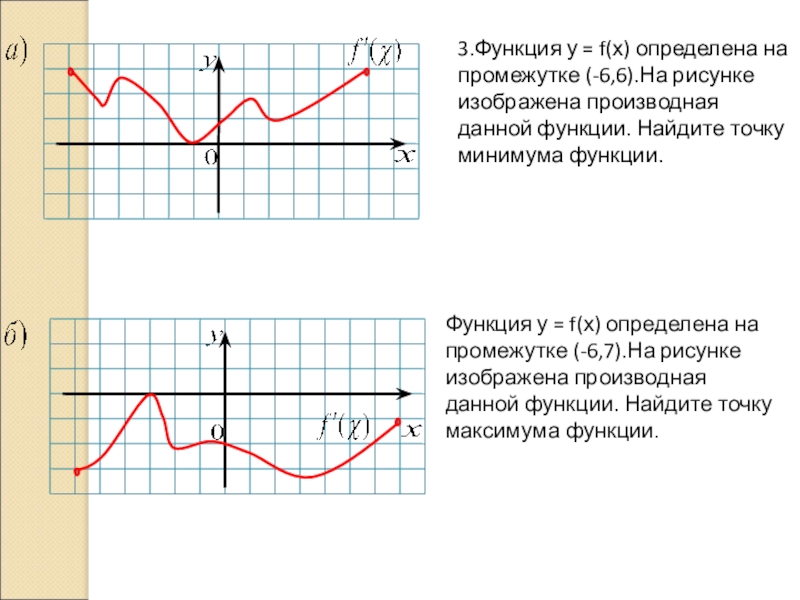
- 21. 3.Функция у = f(х) определена на промежутке
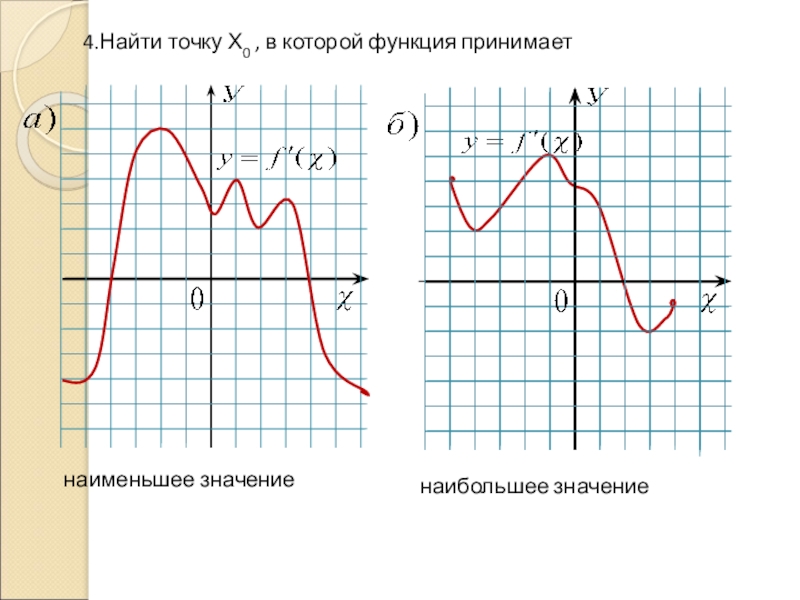
- 22. наименьшее значениенаибольшее значение4.Найти точку Х0 , в которой функция принимает
- 23. 5.Функция у = f(х) определена на отрезке
- 24. 3-тур1.Если точка X0 является точкой экстремума функции,
- 25. Подведение итогов игры
Слайд 1
Брейн-ринг
Производная и ее применение
МБОУ «Орловский УВК»
Учитель математики:
Слайд 3
Понятие производной вошло в математику почти одновременно с понятием функции ,
П. Ферма показал,как решать экстремальные задачи, хотя и не ввел само понятие производной.
Г.В. Лейбниц рассматривал геометрический смысл производной и почти одновременно с И. Ньютоном пришел к понятию производной.
И. Ньютон ввел понятие производной раньше Лейбница ( но опубликовал работы позже). К своим открытиям Лейбниц и Ньютон шли независимо друг от друга. Ньютон исходил в основном из задач механики, а Лейбниц– из геометрических задач.
Эти исследования продолжил Ж.Л. Лагранж , который занимался математическим анализом, вариационным исчислением, теорией чисел. Именно он ввел современное обозначение производной.
Слайд 4
Цель урока: систематизировать и обобщить знания учащихся; развивать логическое мышление, культуру
Слайд 6Вопросы
1.Сформулируйте определение производной функции в точке.
2.В чем состоит геометрический смысл производной?
3.Записать
4.В чем состоит физический смысл производной?
5.Сформулируйте правила дифференцирования.
6.Производные элементарных функций.
7.Какие точки называются критическими?
8.Сформулируйте достаточное условие возрастания (убывания) функции;
постоянства функции
9.Дайте определение точек экстремума функции и ее экстремумов
10.Сформулируйте необходимое и достаточное условия существования
экстремума функции в точке.
11.Дать алгоритм отыскания наибольшего и наименьшего значений функции
y=f(x), непрерывной на отрезке [a;b].
12.По какому алгоритму решается задача на нахождение наибольшего и
наименьшего значений функции на отрезке [a;b].
13.Дать схему исследования и построения графика функции.
Слайд 7
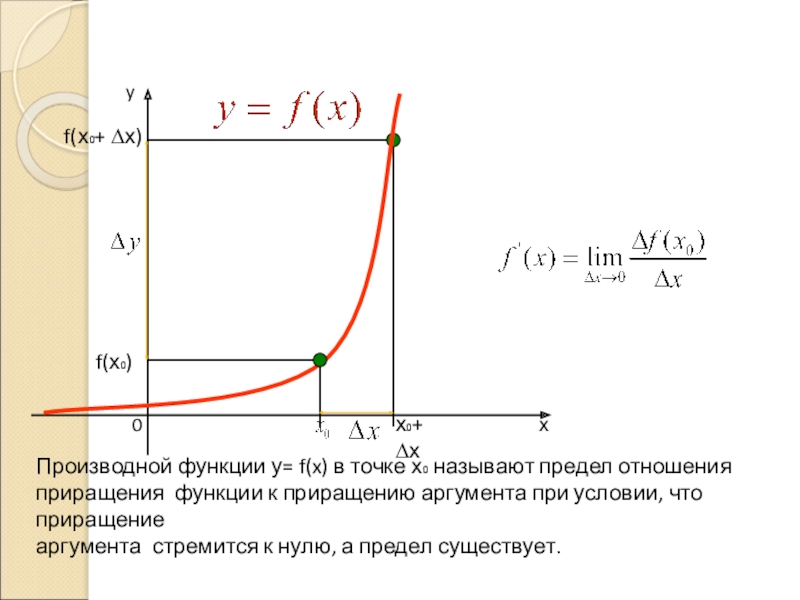
1. Определение производной
Производной функции у=
приращения функции к приращению аргумента при условии, что приращение
аргумента стремится к нулю, а предел существует.
f(х₀)
f(х₀+ ∆х)
х₀+ ∆х
Слайд 8
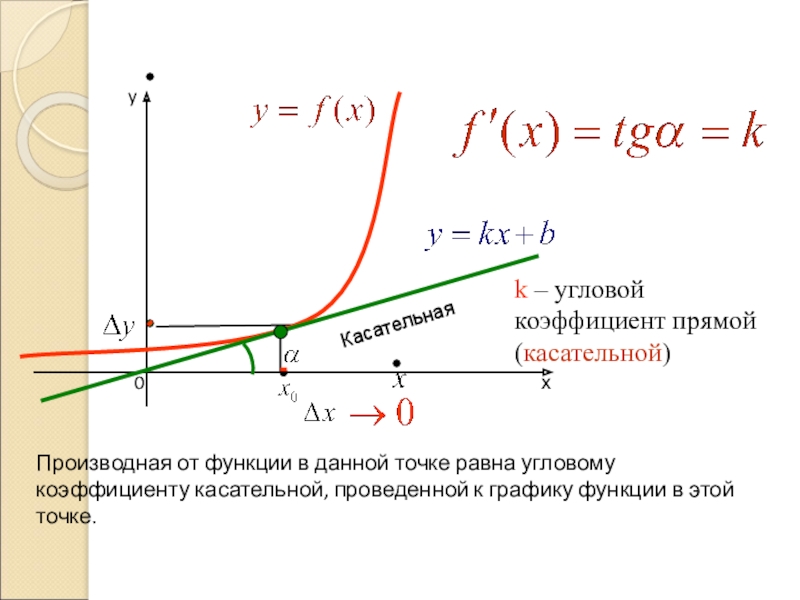
k – угловой коэффициент прямой(касательной)
Касательная
Производная от
2. Геометрический смысл производной
Слайд 10
.
Δх – перемещение тела
Δt – промежуток времени
в течение которого выполнялось
движение
4.Физический смысл
Слайд 115.Правила дифференцирования
Производная суммы(разности)
(u+v)'=u'+v' (u-v)'=u'-v'
Производная произведения
(uv)'=u'v+ uv'
Производная частного
(Сu)’=Cu’
Слайд 13
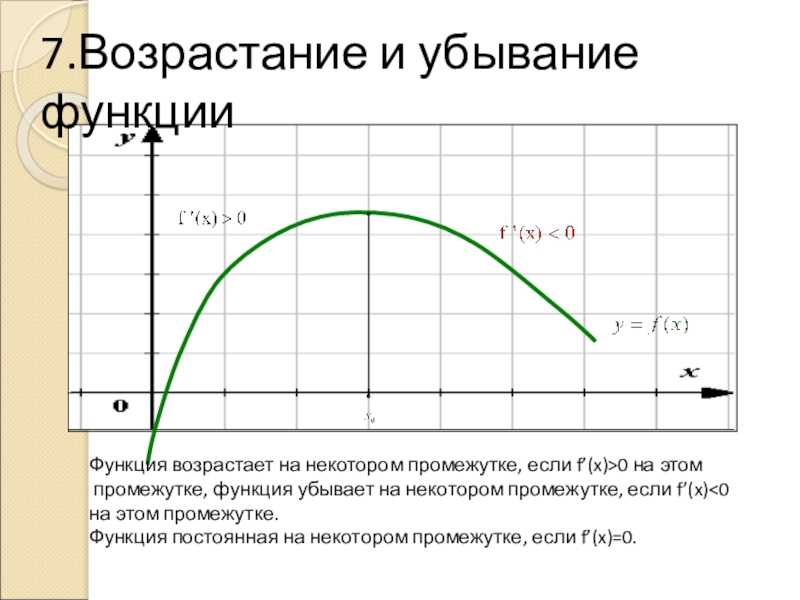
Функция возрастает на некотором промежутке, если f’(x)>0 на этом
промежутке, функция
на этом промежутке.
Функция постоянная на некотором промежутке, если f’(x)=0.
7.Возрастание и убывание функции
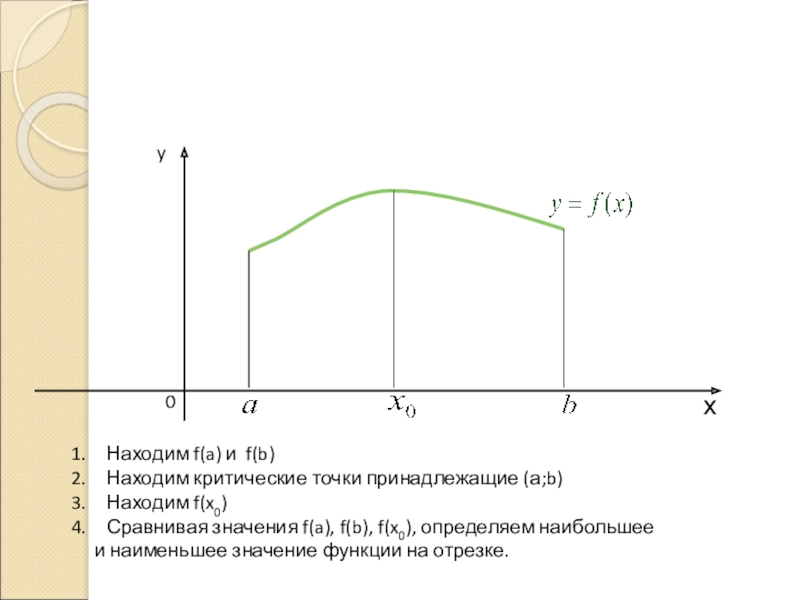
Слайд 159.Наибольшее и наименьшее
значение функции на отрезке
Находим f(a) и f(b)
Находим
Находим f(x0)
Сравнивая значения f(a), f(b), f(x0), определяем наибольшее
и наименьшее значение функции на отрезке.
Слайд 1610.Схема исследования функции и построения графика
1.Найти область определения функции.
2. Определить четность
3. Найти точки пересечения графика функции с осями координат.
4. Определить промежутки знакопостоянства функции.
5. Найти производную и критические точки функции.
6. Найти промежутки возрастания, убывания, точки экстремума и значения функции в этих точках.
7. На основании такого исследования построить график функции.
Слайд 172.Найди производную.
Вариант-1
1. у = х4
2. у = х-7
З.у = 2х3 + 5х
4.у=
5. у= (6-5х)4
6. у = cos х -5
7. у= sin 3x
Вариант-2
1.у = х5
2. у = х-3
3. у = Зх2 - 7х
4.у= (х-3)4
5. у =(3-4х)3
6. у = sin х + 3
7. у=cos5x
Слайд 182-й тур 1.В таблице перепутан порядок записи в третьем и втором столбцах
Слайд 20 2.На рисунке изображен график функции у = f(x) и касательная к
Слайд 213.Функция у = f(х) определена на промежутке (-6,6).На рисунке изображена производная
Функция у = f(х) определена на промежутке (-6,7).На рисунке изображена производная данной функции. Найдите точку максимума функции.
Слайд 23
5.Функция у = f(х) определена на отрезке [-6;6]. График её производной
[-6;6].
Слайд 243-тур
1.Если точка X0 является точкой экстремума функции, то обязательно ли она
2.Вычислите f’(1), если угол между касательной, проведенной к графику функции у=f(х) в точке с абсциссой X0=1, и положительным направлением оси Ох равен 30⁰.
3.Вычислите значение производной функции f(х)=4хlnх+5 при х=е.











![Презентация по алгебре на тему Производная и ее применение (11 класс) 5.Функция у = f(х) определена на отрезке [-6;6]. График её производной 5.Функция у = f(х) определена на отрезке [-6;6]. График её производной изображен на рисунке. Укажите число промежутков](/img/tmb/8/704952/426e19f40aa6f1606ed997f46df0858d-800x.jpg)







