- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку: Понятие первообразной
Содержание
- 1. Презентация к уроку: Понятие первообразной
- 2. Тема урока«Понятие первообразной»учитель математики высшей категорииСеревко И. Д.
- 3. -Сформировать представление о понятии "первообразная", способствовать формированию
- 4. ПЛАН УРОКА
- 5. Найти производную функцийа) ( )' б) ( )' в) ( )' г) ( )' д) ( )' е) ( )'
- 6. Найти производную функций
- 7. Взаимно-обратные операции в математикеОбратнаяСложениеx2Возведение в квадрат sin α
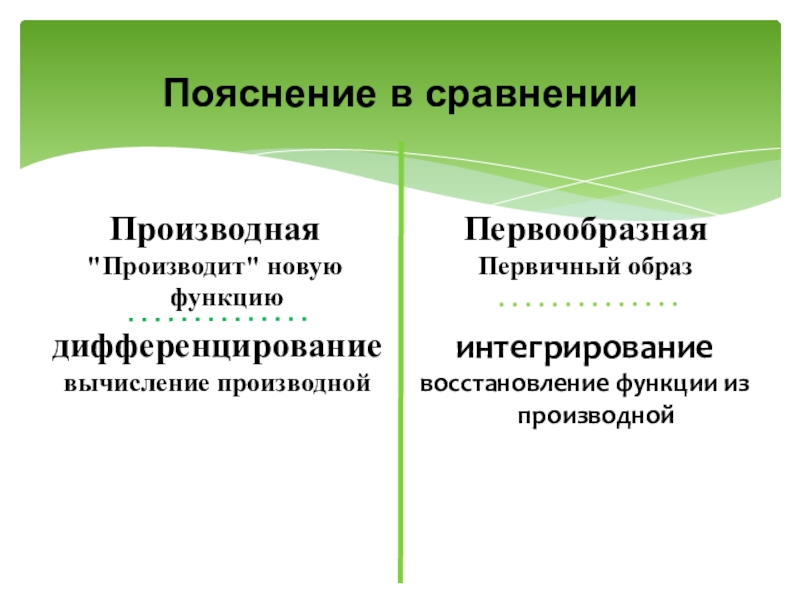
- 8. Пояснение в сравненииПроизводная"Производит" новую функциюПервообразнаяПервичный образдифференцированиевычисление производнойинтегрированиевосстановление функции из производной
- 9. Определение первообразнойy = F(x) называют первообразной для
- 10. Неоднозначность первообразнойf(x) = 2xF1(x) = x2F2(x) =
- 11. Слайд 11
- 12. Правила интегрирования
- 13. Слайд 13
- 14. Задача №6.2 (г) стр. 170 уч. С. М. Никольского.
- 15. №6.8.в) стр.171 уч. С. М. Никольского
- 16. Слайд 16
- 17. 6.П.6.1Первообразная. Памятка.1 уровень: №6.2(д), №6.7(б)2 уровень: №6.5(а), №6.8.(б).Домашнее задание
- 18. Подведение итоговРефлексия
- 19. Спасибо за урок!
Тема урока«Понятие первообразной»учитель математики высшей категорииСеревко И. Д.
Слайд 3-Сформировать представление о понятии "первообразная", способствовать формированию умений применять полученные знания
в новой ситуации. Установить связь между производной и первообразной, формировать умение проверять является ли данная функция первообразной для другой, заданной на некотором числовом промежутке функции.
-развивать навыки мыслительной деятельности при анализе и структурировании учебного материала
-Способствовать привитию культуры умственного труда, воспитывать организованность и сосредоточенность
-развивать навыки мыслительной деятельности при анализе и структурировании учебного материала
-Способствовать привитию культуры умственного труда, воспитывать организованность и сосредоточенность
Цели урока:
Слайд 7Взаимно-обратные операции в математике
Обратная
Сложение
x2
Возведение в квадрат
sin α = a
Синус угла
arcsin a
= α a∈[-1;1]
Арксинус числа
Арксинус числа
Умножение
(xn)' = nxn-1
Дифференцирование
Деление
∫nxn-1dx = xn + C
Интегрирование
Прямая
![Взаимно-обратные операции в математикеОбратнаяСложениеx2Возведение в квадрат sin α = aСинус углаarcsin a = α a∈[-1;1]Арксинус числаУмножение(xn)' =](/img/thumbs/9bddb0d43d8954d4a67f82801c5470aa-800x.jpg "Презентация к уроку: Понятие первообразной Взаимно-обратные операции в математикеОбратнаяСложениеx2Возведение в квадрат sin α = aСинус углаarcsin a")
Слайд 8Пояснение в сравнении
Производная
"Производит" новую функцию
Первообразная
Первичный образ
дифференцирование
вычисление производной
интегрирование
восстановление функции из производной
Слайд 9Определение первообразной
y = F(x) называют первообразной для y = f(x) на
промежутке X, если при x ∈ X
F'(x) = f(x)
F'(x) = f(x)
Слайд 10Неоднозначность первообразной
f(x) = 2x
F1(x) = x2
F2(x) = x2 + 1
F3(x) =
x2 + 5
F1'(x) = 2x
F2'(x) = 2x
F3'(x) = 2x
y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где
C - произвольное число
Слайд 176.П.6.1Первообразная. Памятка.
1 уровень: №6.2(д), №6.7(б)
2 уровень: №6.5(а), №6.8.(б).
Домашнее задание
Слайд 18Подведение итогов
Рефлексия
Все понял
(а), все успел(а)
Частично не понял(а), не все успел(а)
Частично не понял(а), не все успел(а)
