- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии на тему: Параллельность плоскостей (10 класс)
Содержание
- 1. Презентация к уроку геометрии на тему: Параллельность плоскостей (10 класс)
- 2. 1. Две плоскости либо пересекаются по
- 3. 2.
- 4. Доказательство:1. к ІІ β и
- 5. 3.Свойства параллельных плоскостей1. Если две параллельные плоскости
- 6. 2. Отрезки параллельных прямых, заключенные между параллельными
- 7. Задача № 53.Дано: отрезки А1А2; В1В2; С1С2О
- 8. Задача № 53.Решение:Рассмотрим плоскость, проходящую через прямые
- 9. Задача № 54 (самостоятельно записать условие и решить задачу)МРNАВ DC
- 10. ЗАДАЧА № 54
- 11. Домашнее задание:Стр. 20 – 21 п.10, 11
1. Две плоскости либо пересекаются по прямой, либо не пересекаются (не имеют общих точек). Определение: Две плоскости называются параллельными, если они не пересекаются.αβСαβα∩β = сα ІІ β
Слайд 2
1. Две плоскости либо пересекаются по прямой, либо не пересекаются
(не имеют общих точек).
Определение: Две плоскости называются параллельными, если они не пересекаются.
α
β
С
α
β
α∩β = с
α ІІ β
Слайд 3 2. Признак параллельности
двух плоскостей
Теорема: Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
Теорема: Если две пересекающиеся прямые одной плоскости
соответственно параллельны двум прямым другой
плоскости, то эти плоскости параллельны.
к₁
α
β
к
с₁
с
м₁
м
к₁
n
Дано: с ϵ α, к ϵ α, с₁ ϵ β, к₁ ϵ β
к ∩ с = м, к₁ ∩ с₁ = м₁
с ІІ с₁ , к ІІ к₁
Доказать: α ІІ β
Слайд 4Доказательство:
1. к ІІ β и с ІІ β
(по признаку параллельности прямой и
плоскости)
Допустим: α не параллельна β
α ∩ β = n
с ϵ α тогда с ІІ n
с ІІ β
α ∩ β = n
к ϵ α тогда к ІІ n
к ІІ β
Получили: с ІІ n , к ІІ n и к ∩ с = м , но это невозможно,
так как через точку М может проходить только одна прямая,
параллельная прямой n .
Вывод: предположение, что α ∩ β – неверно,
следовательно α ІІ β, что и требовалось доказать.
плоскости)
Допустим: α не параллельна β
α ∩ β = n
с ϵ α тогда с ІІ n
с ІІ β
α ∩ β = n
к ϵ α тогда к ІІ n
к ІІ β
Получили: с ІІ n , к ІІ n и к ∩ с = м , но это невозможно,
так как через точку М может проходить только одна прямая,
параллельная прямой n .
Вывод: предположение, что α ∩ β – неверно,
следовательно α ІІ β, что и требовалось доказать.
Слайд 53.Свойства параллельных плоскостей
1. Если две параллельные плоскости пересечены третьей, то линии
их пересечения параллельны.
Если: α II β
α ∩ γ = а
β ∩ γ = b
ТО: а II b
Если: α II β
α ∩ γ = а
β ∩ γ = b
ТО: а II b
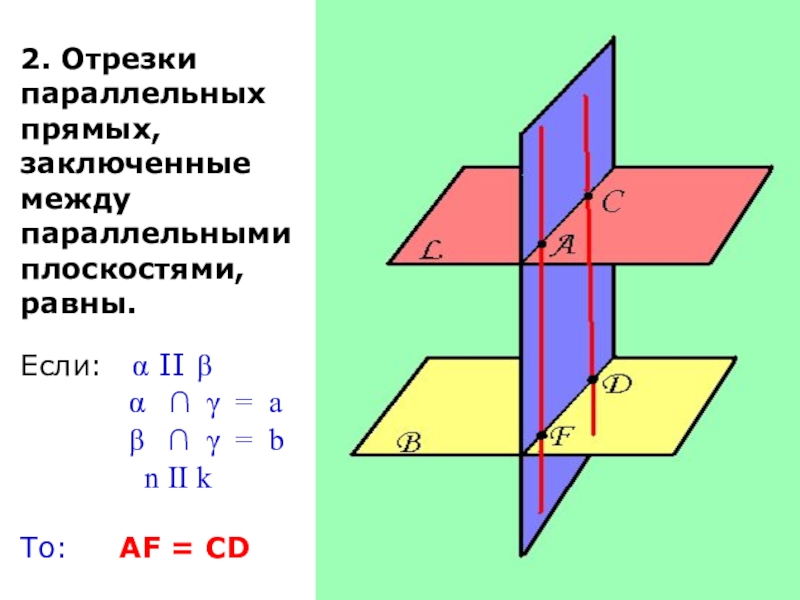
Слайд 62. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Если: α
II β
α ∩ γ = а
β ∩ γ = b
n II k
То: AF = CD
α ∩ γ = а
β ∩ γ = b
n II k
То: AF = CD
Слайд 7Задача № 53.
Дано:
отрезки А1А2; В1В2; С1С2
О Є А1А2; О Є
В1В2;
О ЄС1С2
А1О = ОА2; В1О = ОВ2;
С1О = ОС2
Доказать:
А1В1С1 || А2В2С2
О ЄС1С2
А1О = ОА2; В1О = ОВ2;
С1О = ОС2
Доказать:
А1В1С1 || А2В2С2
А1
В1
А2
В2
С2
С1
О
Слайд 8Задача № 53.
Решение:
Рассмотрим плоскость, проходящую через прямые А₁В₁ и А₂В₂ (такая
плоскость существует, так как прямые пересекаются).
В этой плоскости лежит четырёхугольник А₁В₁А₂В₂, а его диагонали точкой пересечения делятся пополам. Значит — это параллелограмм (по признаку параллелограмма), тогда А₁В₁ II А₂В₂.
Аналогично: из четырёхугольника А₁С₁А₂С₂ → А₁С₁ II А₂С₂.
Вывод: значит плоскости параллельны
А₁В₁С₁ II А₂В₂С₂
В этой плоскости лежит четырёхугольник А₁В₁А₂В₂, а его диагонали точкой пересечения делятся пополам. Значит — это параллелограмм (по признаку параллелограмма), тогда А₁В₁ II А₂В₂.
Аналогично: из четырёхугольника А₁С₁А₂С₂ → А₁С₁ II А₂С₂.
Вывод: значит плоскости параллельны
А₁В₁С₁ II А₂В₂С₂
В2
С1
А1
В1
А2
С2
О
Слайд 10
ЗАДАЧА № 54 (для проверки)
Решение:
а). Так как М — середина АВ, N — середина ВС, то MN = средняя линия ∆АВС. Значит, MN || AC.
Аналогично МР || AD.
Вывод: плоскости MNP || ADC .
б). MN = средняя линия ∆АВС, значит, MN = ½ AC.
Аналогично: NP = ½ CD и MP = ½ AD.
Получим: AC/MN=CD/NP=AD/NP=2/1.
Значит: ▲ACD ∾ ▲MNP, ( коэффициент подобия равен 2), а значит, отношение площадей треугольников
S▲ACD / S▲MNP = 22 = 4.
Следовательно: S▲MNP = S▲ACD : 4 = 48 : 4 = 12 см2.
Ответ: S ▲MNP = 12 см2.
Слайд 11Домашнее задание:
Стр. 20 – 21 п.10, 11 (выучить признак параллельности двух
плоскостей и свойства параллельных плоскостей)
Стр. 22 № 57, № 60
Стр. 22 № 57, № 60