- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку алгебры в 11 классе на тему Применение производной
Содержание
- 1. Презентация к уроку алгебры в 11 классе на тему Применение производной
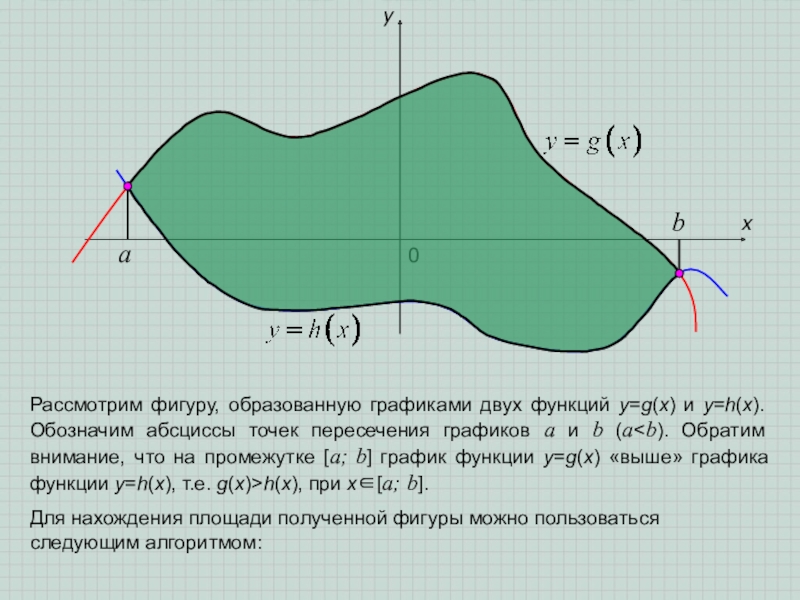
- 2. xy0abРассмотрим фигуру, образованную графиками двух функций y=g(x)
- 3. Найти пределы интегрирования (решить уравнение h(x)=g(x));x0aby2) Составить
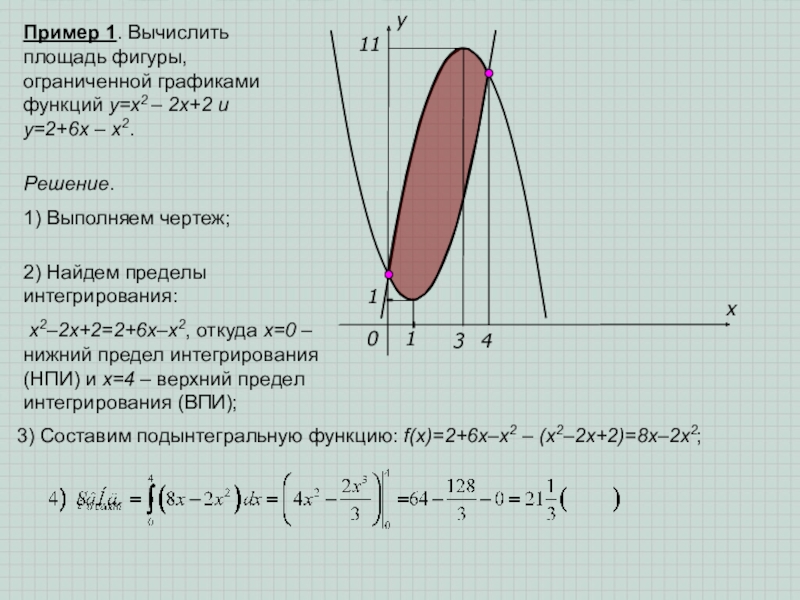
- 4. xy0113114Пример 1. Вычислить площадь фигуры, ограниченной графиками
- 5. 2) Найдем пределы интегрирования: а) x+3= –2x+9
- 6. xy0Пример 3. Вычислить площадь фигуры, ограниченной графиками
- 7. С помощью данного алгоритма можно также находить
Слайд 1Алгебра и начала анализа, 11 класс
Вычисление площадей фигур с помощью интеграла
Воробьев
Слайд 2
x
y
0
a
b
Рассмотрим фигуру, образованную графиками двух функций y=g(x) и y=h(x). Обозначим абсциссы
Для нахождения площади полученной фигуры можно пользоваться следующим алгоритмом:
Слайд 3Найти пределы интегрирования (решить уравнение h(x)=g(x));
x
0
a
b
y
2) Составить подынтегральную положительную на промежутке
3) Вычислить площадь фигуры по формуле:
, где
Разберем несколько примеров применения данного алгоритма.
Слайд 4x
y
0
1
1
3
11
4
Пример 1. Вычислить площадь фигуры, ограниченной графиками функций y=x2 – 2x+2
Решение.
1) Выполняем чертеж;
2) Найдем пределы интегрирования:
x2–2x+2=2+6x–x2, откуда х=0 – нижний предел интегрирования (НПИ) и х=4 – верхний предел интегрирования (ВПИ);
3) Составим подынтегральную функцию: f(x)=2+6x–x2 – (x2–2x+2)=8x–2x2;
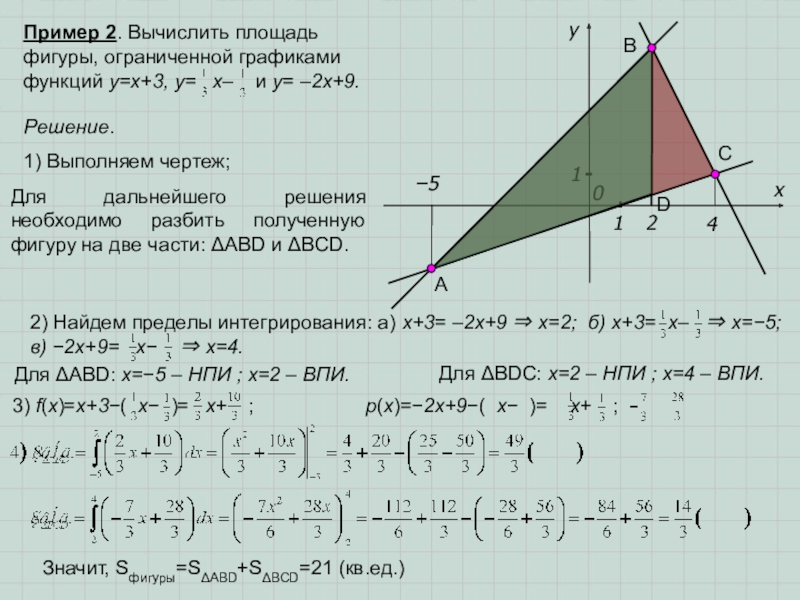
Слайд 52) Найдем пределы интегрирования: а) x+3= –2x+9 ⇒ x=2; б) x+3=
Пример 2. Вычислить площадь фигуры, ограниченной графиками функций y=x+3, y= x– и y= –2x+9.
x
y
0
1
1
2
4
−5
Решение.
1) Выполняем чертеж;
А
В
С
D
Для ΔABD: x=−5 – НПИ ; х=2 – ВПИ.
Для ΔBDС: x=2 – НПИ ; х=4 – ВПИ.
Для дальнейшего решения необходимо разбить полученную фигуру на две части: ΔABD и ΔBCD.
3) f(x)=x+3−( x− )= x+ ; p(x)=−2x+9−( x− )= x+ ;
Значит, Sфигуры=SΔABD+SΔBCD=21 (кв.ед.)
Слайд 6x
y
0
Пример 3. Вычислить площадь фигуры, ограниченной графиками функции y=2x2–8х и двумя
1
1
Решение.
1) Выполняем чертеж;
−8
2
−10
Найдем абсциссы точек касания, используя формулу касательной к графику функции y=f(x) в точке х0: y=f'(x0)(x−x0)+f(x0).
y'=4x−8, −10=(4x0−8)(2−x0)+2x0−8x0 ,откуда х0=1 или 3. Построим касательные.
3
Для дальнейшего рационального решения достаточно вывести уравнение только одной касательной, например, АВ: y=−4(х −1)−6, т.е. y=−4х−2. Тогда, при пределах интегрирования х=1 и х=2, площадь половины фигуры равна:
А
В
С
Значит, площадь всей фигуры равна:
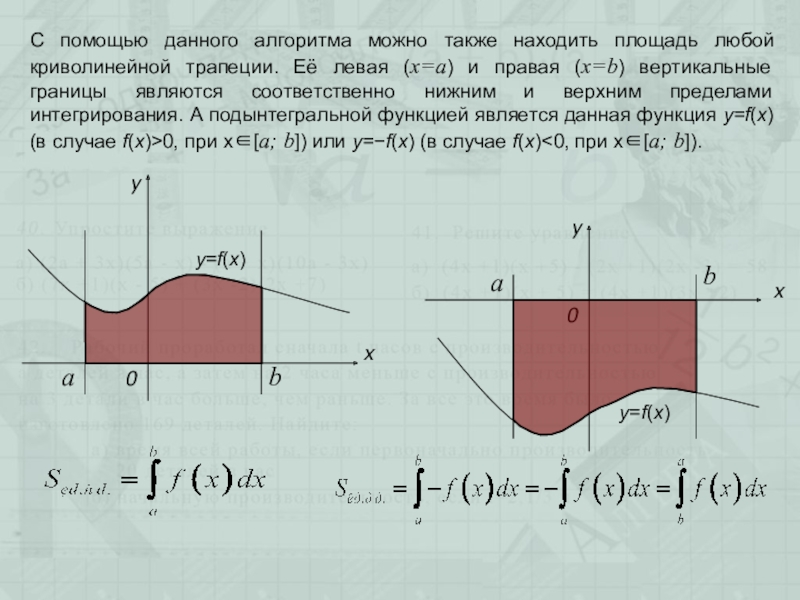
Слайд 7С помощью данного алгоритма можно также находить площадь любой криволинейной трапеции.
y=f(x)
x
y
x
y
0
0
y=f(x)
a
b
a
b

![Презентация к уроку алгебры в 11 классе на тему Применение производной Найти пределы интегрирования (решить уравнение h(x)=g(x));x0aby2) Составить подынтегральную положительную на промежутке Найти пределы интегрирования (решить уравнение h(x)=g(x));x0aby2) Составить подынтегральную положительную на промежутке [a; b] функцию f(x)= g(x)−h(x);3) Вычислить](/img/thumbs/70f6fd03c92a33df99b5d90f55f0e7c6-800x.jpg)