- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад :Экономические задачи егэ по математике
Содержание
- 1. Презентация :Экономические задачи егэ по математике
- 2. Задача.
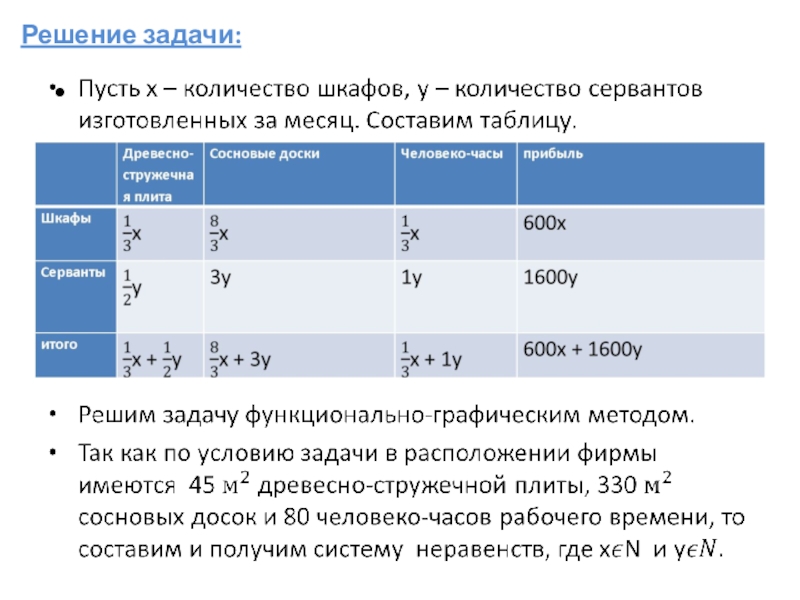
- 3. Решение задачи:
- 4. (продолжения решения задачи)
- 5. Задача на дом.Совхозу требуется не более 10
- 6. Вариант 6.31 декабря 2014 года Алексей взял
- 7. Решение варианта 6:
- 8. Вариант 11.31 декабря 2014 года Арсений взял
- 9. Решение варианта 11:
- 10. (продолжение решения варианта 11)
- 11. Вариант 17.31 декабря 2014 года Михаил взял
- 12. Решение варианта 17:Михаил взял в кредит х
- 13. Вариант 26Матвей хочет взять в кредит 1,4
- 14. Решение варианта 26:Матвей взял в кредит 1,4
- 15. Вариант 4.В июле планируется взять кредит в
- 16. Решение варианта 4:
- 17. (продолжение решения варианта 4)
- 18. Вариант 14.15 января планируется взять кредит в
- 19. Решение варианта 14:
- 20. (продолжение решения варианта 14)
- 21. Вариант 7-15 января планируется взять кредит в
- 22. Решение варианта 7:
- 23. (продолжение решения варианта 7)
- 24. Вариант 32
- 25. Решение варианта 32:
- 26. (продолжение решения варианта 32)
- 27. Вариант 10.У фермера есть два поля, каждое
- 28. Решение варианта 10:Вычислим доход фермера с первого
- 29. Вариант 24.Предприниматель купил здание и собирается в
- 30. Решение варианта 24:1.По максимуму разместим номера «люкс»
- 31. Вариант 33В двух шахтах добывают алюминий и
- 32. Решение варианта 33:Пусть х рабочих 1-ой шахты
- 33. (продолжение решения варианта 33)В промышленности для получения
- 34. Задача по ЕГЭ. Статград, от
- 35. Решение задачи по Стадград от 16.10.2015 года
- 36. Задача 2Иван Михайлович положил 9000 рублей в
- 37. Решение задачи 2:
- 38. Вариант 5В июле планируется взять кредит в
- 39. Решение варианта 5:
- 40. Вариант 815 января планируется взять кредит в
- 41. Решение варианта 8:
- 42. (продолжение решения варианта 8)
- 43. Задача. В банк помещена сумма 3900 тысяч
- 44. Решение задачи:50% годовых означает, что каждый год
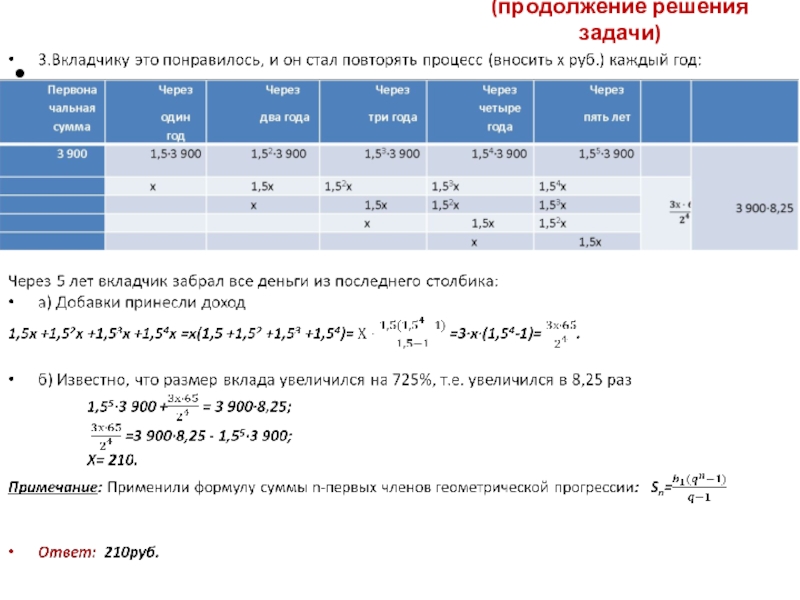
- 45. (продолжение решения задачи)
- 46. Задача 2.15-го января был выдан полугодовой кредит
- 47. Решение задачи 2:Представим таблицей реальную ситуацию, описанную в условии задачи:15%+14,5%+14%+13,5%+13%+52,5% =122,5%122,5% - 100% = 22,5%Ответ: 22,5.
- 48. Спасибо за внимание!
Задача.
Слайд 5Задача на дом.
Совхозу требуется не более 10 трехтонных автомашин и не
более 8 пятитонных. Отпускная цена на машины первой марки 200 тыс.рублей, второй марки 400 тыс.рублей.
Совхоз может выделить для приобретения автомашин 4 млн.рублей.
Сколько следует приобрести автомашин каждой марки в отдельности, чтобы их общая (суммарная) грузоподъемность была максимальной.
Совхоз может выделить для приобретения автомашин 4 млн.рублей.
Сколько следует приобрести автомашин каждой марки в отдельности, чтобы их общая (суммарная) грузоподъемность была максимальной.
Слайд 6Вариант 6.
31 декабря 2014 года Алексей взял в банке 9 282 000 рублей
в кредит под 10 % годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Алексей переводит в банк X рублей.
Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Какой должна быть сумма X, чтобы Алексей выплатил долг четырьмя равными платежами (то есть за четыре года)?
Слайд 8Вариант 11.
31 декабря 2014 года Арсений взял в банке 1 000 000 рублей
в кредит. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определенное количество процентов), затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй 638,4 тыс. рублей.
Под какой процент банк выдал кредит Арсению?
Под какой процент банк выдал кредит Арсению?
Слайд 11Вариант 17.
31 декабря 2014 года Михаил взял в банке некоторую сумму
в кредит под 10% годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Михаил переводит в банк 2 928 200 рублей.
Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Какую сумму взял Михаил в банке, если он выплатил долг четырьмя равными платежами (то есть за четыре года)?
Слайд 12Решение варианта 17:
Михаил взял в кредит х рублей под 10%
1 год:
х * 1,1 – 2 928 200 (осталось платить)
2 год: (1,1х – 2 928 200) * 1,1 – 2 928 200 = 1,12х – 2 928 200(1,1 + 1) =
=1,12х – 2,1 * 2 928 200 (осталось)
3 год: (1,12х – 2,1 * 2 928 200) * 1,1 – 2 928 200 =
=1,13х – 2 928 200(2,1 * 1,1 +1) = 1,13х – 3,31 * 2 928 200 (осталось)
4 год: (1,13х – 3,31 * 2 928 200)* 1,1 – 2 928 200 =
=1,14х – 2 928 200(3,31 * 1,1 +1) = 1,14х – 2 928 200 * 4,641 = 0 (кредит погашен)
Решим уравнение:
1,14х – 2 928 200 * 4,641 = 0
1,14х = 2 928 200 * 4,641
1,4641х=13 589 776
х = 13 589 776 : 1, 4641
х = 9 282 000
Ответ: 9 282 000 рублей взял Михаил в банке
2 год: (1,1х – 2 928 200) * 1,1 – 2 928 200 = 1,12х – 2 928 200(1,1 + 1) =
=1,12х – 2,1 * 2 928 200 (осталось)
3 год: (1,12х – 2,1 * 2 928 200) * 1,1 – 2 928 200 =
=1,13х – 2 928 200(2,1 * 1,1 +1) = 1,13х – 3,31 * 2 928 200 (осталось)
4 год: (1,13х – 3,31 * 2 928 200)* 1,1 – 2 928 200 =
=1,14х – 2 928 200(3,31 * 1,1 +1) = 1,14х – 2 928 200 * 4,641 = 0 (кредит погашен)
Решим уравнение:
1,14х – 2 928 200 * 4,641 = 0
1,14х = 2 928 200 * 4,641
1,4641х=13 589 776
х = 13 589 776 : 1, 4641
х = 9 282 000
Ответ: 9 282 000 рублей взял Михаил в банке
Слайд 13Вариант 26
Матвей хочет взять в кредит 1,4 млн рублей. Погашение кредита
происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка процента 10% годовых.
На какое минимальное количество лет может Матвей взять кредит, чтобы ежегодные выплаты были не более 320 тысяч рублей?
На какое минимальное количество лет может Матвей взять кредит, чтобы ежегодные выплаты были не более 320 тысяч рублей?
Слайд 14Решение варианта 26:
Матвей взял в кредит 1,4 млн рублей под 10%
0
год: 1 400 000 рублей
1 год: 1 400 000 ∙1,1 – 320 000=1 220 000
2 год: 1 220 000 ∙ 1,1 – 320 000 = 1 022 000
3 год: 1 022 000 ∙ 1,1 – 320 000 = 804 200
4 год: 804 200 ∙ 1,1 – 320 000 = 564 200
5 год: 564 200 ∙ 1,1 – 320 000 = 301 082
6 год: 301 082 ∙ 1,1 – 320 000 = 11 190,2
7 год: 11 190,2 ∙ 1,1 – 320 000 = 0
Значит, Матвей погасит кредит за 7 лет
Ответ: 7 лет
1 год: 1 400 000 ∙1,1 – 320 000=1 220 000
2 год: 1 220 000 ∙ 1,1 – 320 000 = 1 022 000
3 год: 1 022 000 ∙ 1,1 – 320 000 = 804 200
4 год: 804 200 ∙ 1,1 – 320 000 = 564 200
5 год: 564 200 ∙ 1,1 – 320 000 = 301 082
6 год: 301 082 ∙ 1,1 – 320 000 = 11 190,2
7 год: 11 190,2 ∙ 1,1 – 320 000 = 0
Значит, Матвей погасит кредит за 7 лет
Ответ: 7 лет
Слайд 15Вариант 4.
В июле планируется взять кредит в банке на сумму 16
млн рублей на некоторый срок ( целое число лет). Условия его возврата таковы:
каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
с февраля по июнь каждого года необходимо выплатить часть долга;
в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
с февраля по июнь каждого года необходимо выплатить часть долга;
в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Слайд 18Вариант 14.
15 января планируется взять кредит в банке на 24 месяца.
Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего года;
-со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е числа предыдущего месяца.
Известно, что в течении второго года кредитования нужно вернуть банку 339.тыс рублей.
Какую сумму нужно вернуть банку в течении первого года кредитования?
-1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего года;
-со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е числа предыдущего месяца.
Известно, что в течении второго года кредитования нужно вернуть банку 339.тыс рублей.
Какую сумму нужно вернуть банку в течении первого года кредитования?
Слайд 21Вариант 7
-15 января планируется взять кредит в банке на 21 месяц.
Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей.
Какую сумму нужно вернуть банку в течение всего срока кредитования?
-1-го числа каждого месяца долг возрастает на 1% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей.
Какую сумму нужно вернуть банку в течение всего срока кредитования?
Слайд 27Вариант 10.
У фермера есть два поля, каждое площадью 10 гектаров. На
каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором – 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га.
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу – по цене 8000 руб. за центнер.
Какой наибольший доход может получить фермер?
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу – по цене 8000 руб. за центнер.
Какой наибольший доход может получить фермер?
Слайд 28Решение варианта 10:
Вычислим доход фермера с первого поля, если он засеет
на нем картофель.
Урожайность картофеля на нем 500 ц/га, цена картофеля 5000 за центнер, размер поля 10 гектар, получаем размер дохода
5000∙500∙10=25 000 000 руб.
Теперь сравним доход, если на первом поле будет засеяна свекла, получим
8000∙300∙10=24 000 000 руб.
Отсюда видно, что на первом поле выгоднее сажать картофель.
Аналогично сравним доход, приносимый вторым полем:
- для картофеля:
5000∙300∙10=15 000 000 руб;
- для свёклы:
8000∙500∙10=40 000 000 руб.
Следовательно, на втором поле выгоднее сажать свёклу.
Таким образом, максимально возможный доход фермер может получить в сумме
25 000 000+40 000 000=65 000 000 руб.
Ответ: 65 000 000 руб.
Урожайность картофеля на нем 500 ц/га, цена картофеля 5000 за центнер, размер поля 10 гектар, получаем размер дохода
5000∙500∙10=25 000 000 руб.
Теперь сравним доход, если на первом поле будет засеяна свекла, получим
8000∙300∙10=24 000 000 руб.
Отсюда видно, что на первом поле выгоднее сажать картофель.
Аналогично сравним доход, приносимый вторым полем:
- для картофеля:
5000∙300∙10=15 000 000 руб;
- для свёклы:
8000∙500∙10=40 000 000 руб.
Следовательно, на втором поле выгоднее сажать свёклу.
Таким образом, максимально возможный доход фермер может получить в сумме
25 000 000+40 000 000=65 000 000 руб.
Ответ: 65 000 000 руб.
Слайд 29Вариант 24.
Предприниматель купил здание и собирается в нем открыть отель. В
отеле могут быть стандартные номера площадью 30 квадратных метров и номера "люкс" площадью 40 квадратных метров.Общая площадь. которую можно отвести под номера , составляет 940 квадратных метров.
Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер "люкс" - 5000 рублей в сутки.
Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в сутки, а номер "люкс" - 5000 рублей в сутки.
Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Слайд 30Решение варианта 24:
1.По максимуму разместим номера «люкс» в отеле.
940 = 22∙40
+ 2∙30.
Имеем 22 номера «люкс» и 2 стандартных номера.
Их общая стоимость составит
22∙5000 + 2∙4000 = 118 000 рублей.
2.По максимуму разместим стандартные номера в отеле.
940 = 30∙30 + 1∙40.
Имеем 30 стандартных номеров и 1 номер «люкс».
Их общая стоимость составит
30∙4000 + 1∙5000 = 125 000 рублей.
Ответ: 125 000 рублей.
Имеем 22 номера «люкс» и 2 стандартных номера.
Их общая стоимость составит
22∙5000 + 2∙4000 = 118 000 рублей.
2.По максимуму разместим стандартные номера в отеле.
940 = 30∙30 + 1∙40.
Имеем 30 стандартных номеров и 1 номер «люкс».
Их общая стоимость составит
30∙4000 + 1∙5000 = 125 000 рублей.
Ответ: 125 000 рублей.
Слайд 31Вариант 33
В двух шахтах добывают алюминий и никель. В первой шахте
имеется 20 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 2 кг никеля. Во второй шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 1 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплавов.
Сколько кг сплава при таких условиях ежедневно сможет произвести завод?
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплавов.
Сколько кг сплава при таких условиях ежедневно сможет произвести завод?
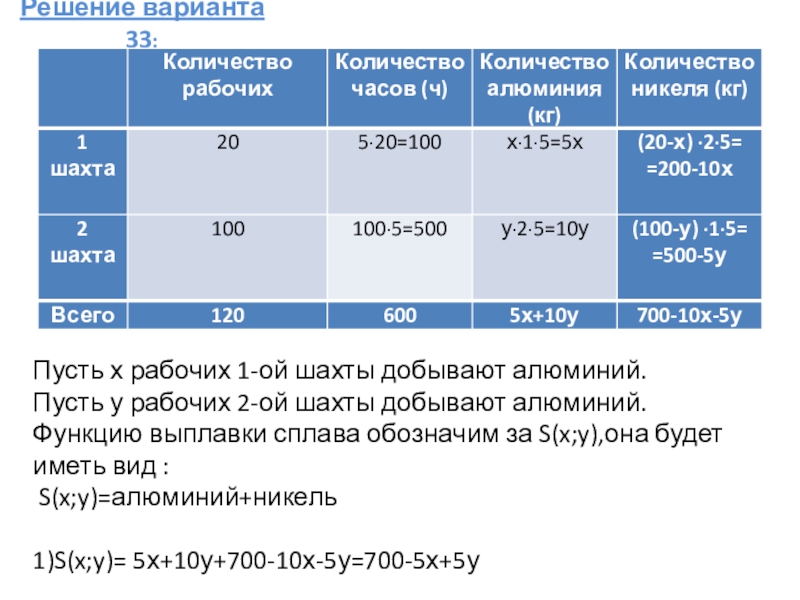
Слайд 32Решение варианта 33:
Пусть х рабочих 1-ой шахты добывают алюминий.
Пусть у рабочих
2-ой шахты добывают алюминий.
Функцию выплавки сплава обозначим за S(x;y),она будет иметь вид :
S(x;y)=алюминий+никель
1)S(x;y)= 5х+10у+700-10х-5у=700-5х+5у
Функцию выплавки сплава обозначим за S(x;y),она будет иметь вид :
S(x;y)=алюминий+никель
1)S(x;y)= 5х+10у+700-10х-5у=700-5х+5у
Слайд 33(продолжение решения варианта 33)
В промышленности для получения сплава нужно в 2
раза больше алюминия, чем никеля, тогда составим уравнение:
2)5х+10у=2(700-10х-5у)
5х+10у=1400-20х-10у
25х+20у-1400=0
20у=1400-25х
у=(1400-25х):20
у=70-1,25х
3) S(x)=700-5x+5(70-1,25x)=1050-5x-6,25x=1050-11,25x
Получим: 1050-11,25x – убывающая функция, отсюда х=0 max S(x)=S(0)=1050. Значит 1050 кг сплава ежедневно будет выпускать промышленность.
Ответ:1 050
2)5х+10у=2(700-10х-5у)
5х+10у=1400-20х-10у
25х+20у-1400=0
20у=1400-25х
у=(1400-25х):20
у=70-1,25х
3) S(x)=700-5x+5(70-1,25x)=1050-5x-6,25x=1050-11,25x
Получим: 1050-11,25x – убывающая функция, отсюда х=0 max S(x)=S(0)=1050. Значит 1050 кг сплава ежедневно будет выпускать промышленность.
Ответ:1 050
Слайд 34
Задача по ЕГЭ. Статград,
от 16.10.2015 года.
15 января был выдан кредит
на приобретение легкового автомобиля. В таблице указан график его погашения. Текущий долг указан в процентах от кредита.
В конце каждого месяца, начиная с января, долг увеличивается на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля.
На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
В конце каждого месяца, начиная с января, долг увеличивается на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля.
На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Слайд 36Задача 2
Иван Михайлович положил 9000 рублей в банк «Достояние» с хорошей
процентной ставкой. По истечении года к его вкладу были причислены процентные деньги, и в то же время он увеличил свой вклад на 1280 рублей. Еще через год после начисления процентов по вкладу он решил снять 1600 рублей, а остальные 10280 рублей положил на новый срок.
Чему равна процентная ставка в этом банке?
Чему равна процентная ставка в этом банке?
Слайд 38Вариант 5
В июле планируется взять кредит в банке на сумму 4,5
млн рублей на срок 9 лет.
Условия его возврата таковы:
-каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо выплатить часть долга;
-в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платеж по кредиту составит не более 1,4 млн рублей, а наименьший-не менее 0,6 млн рублей.
Условия его возврата таковы:
-каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
-с февраля по июнь каждого года необходимо выплатить часть долга;
-в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платеж по кредиту составит не более 1,4 млн рублей, а наименьший-не менее 0,6 млн рублей.
Слайд 40Вариант 8
15 января планируется взять кредит в банке на 24 месяца.
Условия его возврата таковы:
-первого числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
-со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
-15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течении первого года кредитования нужно вернуть банку 466,5 тыс. рублей.
Какую сумму планируется взять в кредит?
-первого числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
-со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
-15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что в течении первого года кредитования нужно вернуть банку 466,5 тыс. рублей.
Какую сумму планируется взять в кредит?
Слайд 43Задача.
В банк помещена сумма 3900 тысяч рублей под 50% годовых.
В конце каждого из первых четырех лет хранения после вычисления процентов вкладчик дополнительно вносил на счет одну и ту же фиксированную сумму. К концу пятого года, после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 725%.
Какую сумму вкладчик ежегодно добавлял к вкладу?
Какую сумму вкладчик ежегодно добавлял к вкладу?
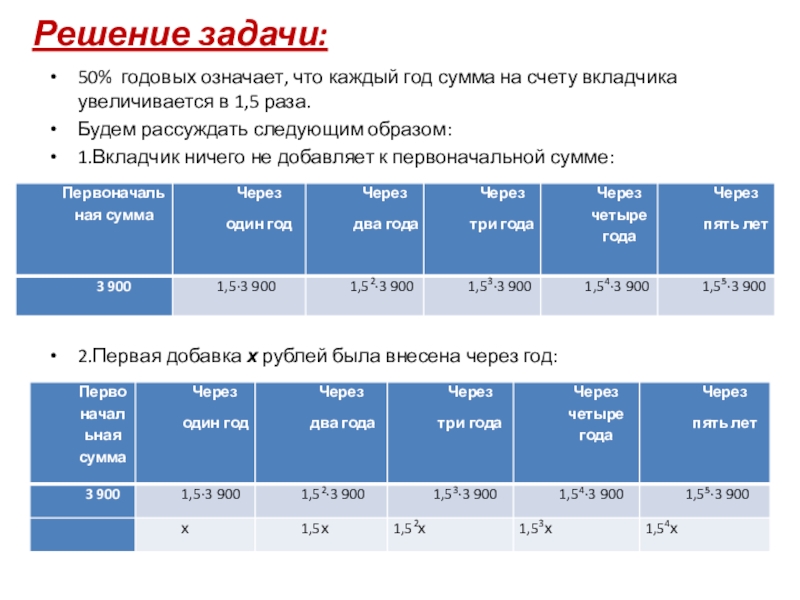
Слайд 44Решение задачи:
50% годовых означает, что каждый год сумма на счету вкладчика
увеличивается в 1,5 раза.
Будем рассуждать следующим образом:
1.Вкладчик ничего не добавляет к первоначальной сумме:
2.Первая добавка х рублей была внесена через год:
Будем рассуждать следующим образом:
1.Вкладчик ничего не добавляет к первоначальной сумме:
2.Первая добавка х рублей была внесена через год:
Слайд 46Задача 2.
15-го января был выдан полугодовой кредит на развитие бизнеса. В
таблице представлен график его погашения:
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
В конце каждого месяца, начиная с января, текущий долг увеличивался на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
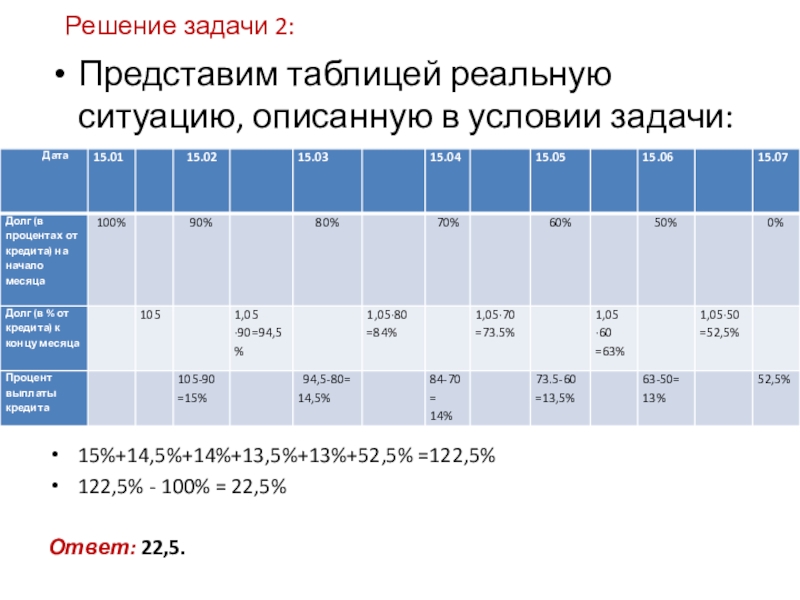
Слайд 47Решение задачи 2:
Представим таблицей реальную ситуацию, описанную в условии задачи:
15%+14,5%+14%+13,5%+13%+52,5% =122,5%
122,5%
- 100% = 22,5%
Ответ: 22,5.
Ответ: 22,5.