- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по высшей математике на тему Дифференциал функций
Содержание
- 1. Презентация по высшей математике на тему Дифференциал функций
- 2. План лекцииДифференциал функции. Геометрический смысл дифференциала.Частные производные. Полный дифференциал. Применение дифференциала в приближенных вычислениях. Исследование функций.
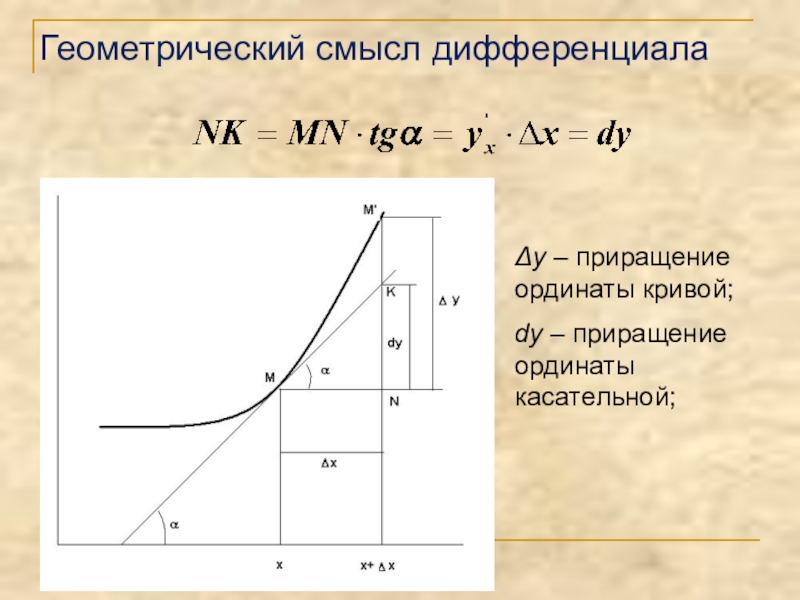
- 3. Δy – приращение ординаты кривой; dy – приращение ординаты касательной; Геометрический смысл дифференциала
- 4. ДифференциалДифференциал dy - главная часть бесконечно малого
- 5. Вычисление дифференциалов
- 6. Дифференциалы сложных функций
- 7. Приближенные вычисления с помощью дифференциалаЗначение функции в
- 8. Функции нескольких переменных. Частная производнаяОбъем кругового цилиндраФункция n переменныхЧастная производная по х
- 9. Исследование функций
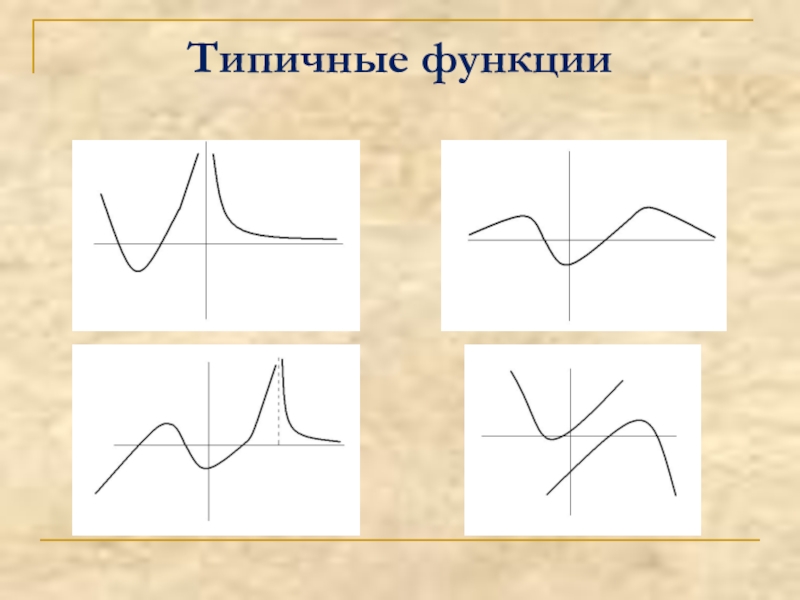
- 10. Типичные функции
- 11. Основные характеристики и свойства функции Y=f(X) Область
- 12. Постоянство и монотонность функцииДля того чтобы функция
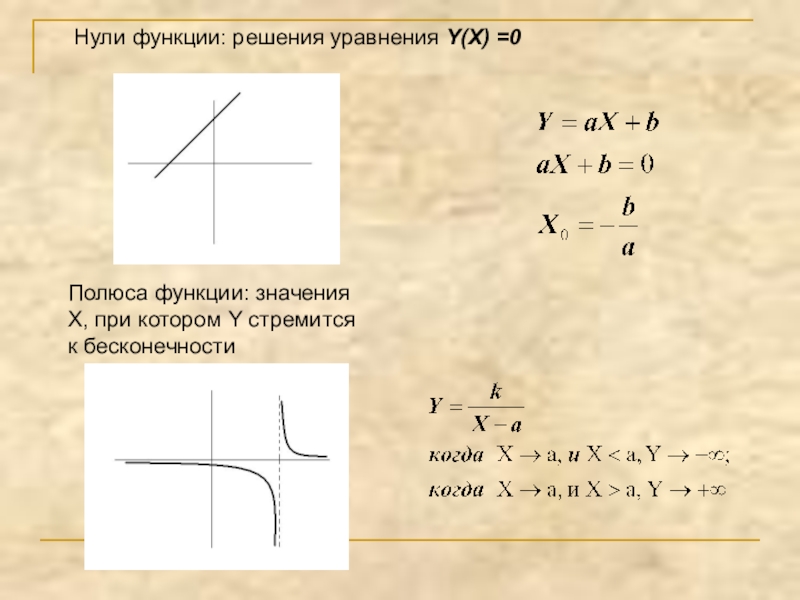
- 13. Нули функции: решения уравнения Y(X) =0Полюса функции: значения Х, при котором Y стремится к бесконечности
- 14. Минимумы и максимумы функцииФункция f(x) имеет в
- 15. Правило нахождения экстремума
- 16. Перегибы, выпуклость и вогнутость функцииЕсли вторая производная
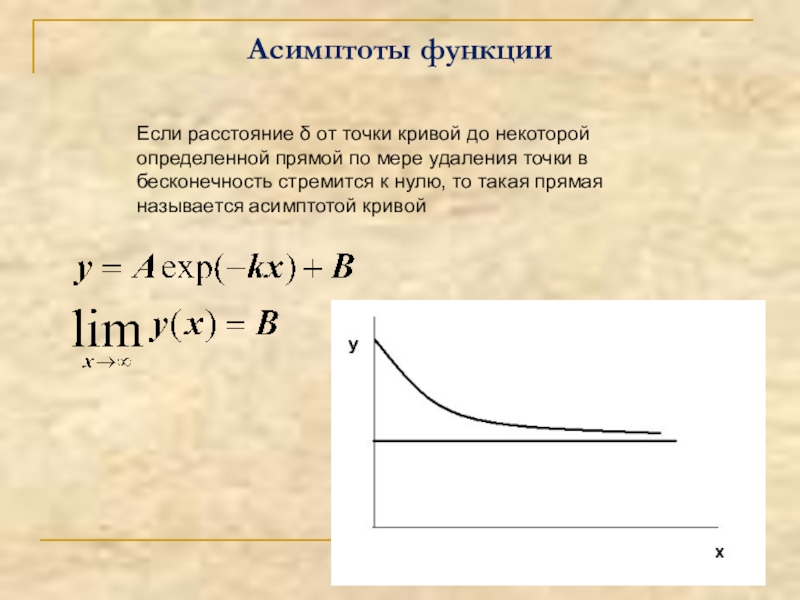
- 17. Асимптоты функцииЕсли расстояние δ от точки кривой
- 18. Основная литература:Ганичева А.В., Козлов В.П. Математика для
Слайд 2План лекции
Дифференциал функции. Геометрический смысл дифференциала.
Частные производные. Полный дифференциал.
Применение дифференциала
Исследование функций.
Слайд 3Δy – приращение ординаты кривой;
dy – приращение ординаты касательной;
Геометрический
Слайд 4Дифференциал
Дифференциал dy - главная часть бесконечно малого приращения функции Δy
Дифференциалом dx
Слайд 7Приближенные вычисления с помощью дифференциала
Значение функции в точке Δх, близкой к
Положим х0=2.3 и Δх=0.1. Тогда Δy=2.42 – 2.32=1.657
dy=3·2.32·0.1=1.587
Слайд 8Функции нескольких переменных. Частная производная
Объем кругового цилиндра
Функция n переменных
Частная производная по
Слайд 11Основные характеристики и свойства функции Y=f(X)
Область значений y и х
Постоянство или монотонность функции на отрезке - Нули функций
Разрывы и полюса функции
Экстремумы, минимумы и максимумы функции
Перегибы функции
Асимптоты функции
Вогнутость и выпуклость функции
Слайд 12Постоянство и монотонность функции
Для того чтобы функция f(x) была постоянной на
Для того, чтобы функция f(x) была монотонной на отрезке [a,b], нужно чтобы производная не меняла своего знака на этом отрезке и не обращалась тождественно в нуль ни в какой точке или промежутке, составляющем часть отрезка.
Слайд 13Нули функции: решения уравнения Y(X) =0
Полюса функции: значения Х, при котором
Слайд 14Минимумы и максимумы функции
Функция f(x) имеет в точке х0 минимум (максимум),
Экстремум = минимум или максимум
Необходимое, но недостаточное условие существования экстремума: экстремум функции достигается в точках, где значение производной равно нулю.
Контр-пример:
Достаточное условие:
Если первая производная в точке х0 равна нулю, а вторая производная - больше нуля, то функция имеет минимум;
Если первая производная в точке х0 равна нулю, а вторая производная меньше нуля, то функция имеет максимум
Слайд 16Перегибы, выпуклость и вогнутость функции
Если вторая производная в точке М больше
Если вторая производная в точке М меньше нуля, то кривая в той точке вогнутостью направлена вниз.
Если вторая производная в точке М равна нулю, то М – точка перегиба
Слайд 17Асимптоты функции
Если расстояние δ от точки кривой до некоторой определенной прямой
Слайд 18
Основная литература:
Ганичева А.В., Козлов В.П. Математика для психологов. М.: Аспект-пресс, 2005,
Павлушков И.В. Основы высшей математики и математической статистики. М., ГЭОТАР-Медиа, 2007.
Журбенко Л. Математика в примерах и задачах. М.: Инфра-М, 2009.









![Презентация по высшей математике на тему Дифференциал функций Постоянство и монотонность функцииДля того чтобы функция f(x) была постоянной на Постоянство и монотонность функцииДля того чтобы функция f(x) была постоянной на отрезке [a,b], нужно, чтобы производная этой](/img/thumbs/d93138646c040a04e79c0c1205c96e36-800x.jpg)