- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине Основы теории информации для специальности Прикладная информатика (по отраслям) на тему Системы счисления
Содержание
- 1. Презентация по дисциплине Основы теории информации для специальности Прикладная информатика (по отраслям) на тему Системы счисления
- 2. Слайд 2
- 3. Непозиционные системы счисления
- 4. Период палеолита. 10-11 тысяч лет до н.э.
- 5. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯДревнеегипетская десятичная непозиционная СС- единицы-
- 6. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯВавилонская СС – шестидесятеричная (2000
- 7. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ= 33 2-ойразряд1-ыйразряд=
- 8. Запишите в Вавилонской системе счисления следующие числа: 47491203
- 9. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ До наших дней сохранились следы
- 10. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯАлфавитные системы счисленияВ древнейшее время
- 11. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯРимская (500 лет до
- 12. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯПредставить число 444 в римской
- 13. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯКакое число спрятали римляне?MCMLXXIV =
- 14. Запишите в Римской системе счисления следующие числа:2000201719991537945950
- 15. Какие числа записаны в Римской системе счисления?CXIXMLMCCMXCVIIMCDIV
- 16. До XVII века эта форма записи чисел
- 17. Коротко о главном К НЕПОЗИЦИОННЫМ системам
- 18. Позиционные системы счисления
- 19. Позиционной называют систему счисления, в которой число
- 20. Позиционные системы счисленияСмешанные: p-q-ичныеКаждая цифра числа, заданного
- 21. Позиционные системы счисленияРазвернутая форма записи числаСвернутая форма
- 22. Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716) немецкий философ,
Слайд 4Период палеолита. 10-11 тысяч лет до н.э.
Единичная система счисления
Единичная
Появились специальные обозначения для «пятерок», «десяток», «сотен» и т.д.
Слайд 5НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Древнеегипетская десятичная непозиционная СС
- единицы
- десятки
- сотни
= 3
Возникла во второй половине
третьего тысячелетия до н.э.
Слайд 6НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Вавилонская СС – шестидесятеричная (2000 лет до н.э.)
Прямой клин
Лежачий клин (десятки)
60; 602; 603; …; 60n
Для определения значения числа
нужно его изображение разбить на разряды слева направо. Значение числа определяли по значениям составляющих его «цифр», но с учетом того, что «цифры» в каждом последующем разряде значили в 60 раз больше тех же «цифр» в предыдущем разряде.
Слайд 7НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
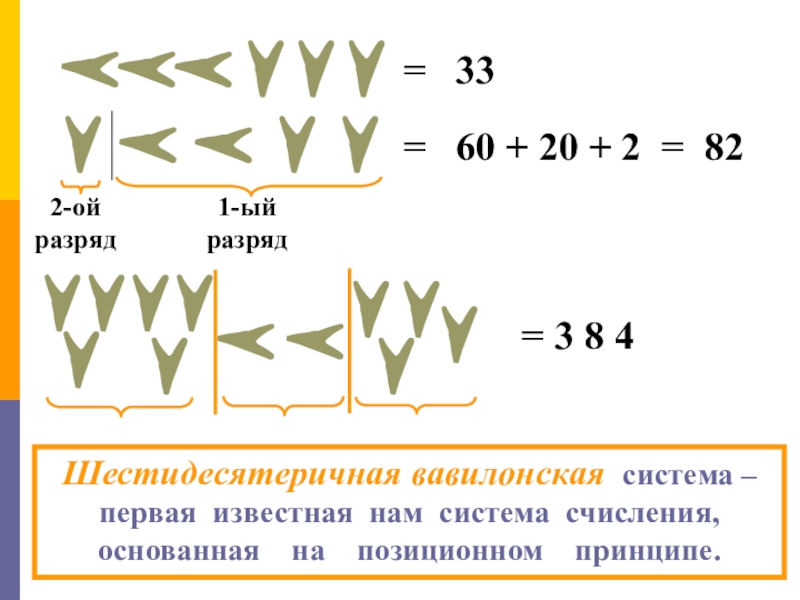
= 33
2-ой
разряд
1-ый
разряд
= 60 + 20 +
3 8 4
=
Шестидесятеричная вавилонская система – первая известная нам система счисления,
основанная на позиционном принципе.
Слайд 9НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
До наших дней сохранились следы счета шестидесятками.
час -
минута - 60 секунд.
Окружность -360, то есть 6*60 градусов,
градус - 60 минут
минута - шестьдесят секунд.
Слайд 10НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
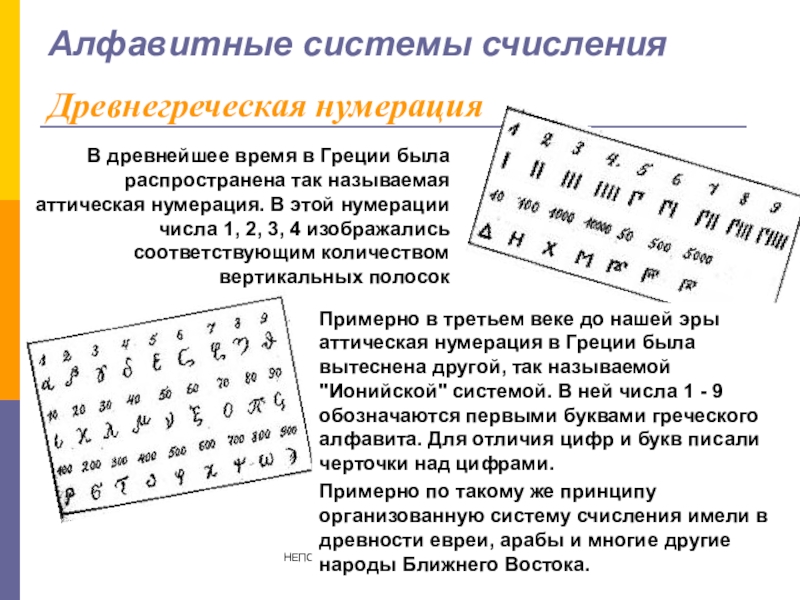
Алфавитные системы счисления
В древнейшее время в Греции была распространена
Древнегреческая нумерация
Примерно в третьем веке до нашей эры аттическая нумерация в Греции была вытеснена другой, так называемой "Ионийской" системой. В ней числа 1 - 9 обозначаются первыми буквами греческого алфавита. Для отличия цифр и букв писали черточки над цифрами.
Примерно по такому же принципу организованную систему счисления имели в древности евреи, арабы и многие другие народы Ближнего Востока.
Слайд 11НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Римская
(500 лет до н.э.)
Цифры:
Эта римская
древняя табличка
написана 2000
Число обозначается набором подряд стоящих «цифр»
Значение числа равно:
1). Сумме значений идущих подряд нескольких
одинаковых «цифр»: ХХ=20
2). Разности значений двух «цифр», если слева от
большей «цифры» стоит меньшая:
СМ = 1000 – 100 = 900
Слайд 12НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Представить число 444 в римской СС.
4 4 4 =
(D-C)
+
+ (V-I)
= 400 + 40 + 4
400
CD
40
XL
4
IV
444=CDXLIV
Слайд 13НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Какое число спрятали римляне?
MCMLXXIV = ?
M C M L
1000 +
(M-C) = 1000 - 100 = 900 +
50 +
20 +
4
1974
Слайд 16До XVII века эта форма записи чисел была официальной на территории
Славянская кириллическая нумерация
Для записи чисел от 1 до 10 использовались
первые буквы алфавита, над которыми ставился
специальный знак – титло
Аз - 1
Веди - 2
Глаголь - 3
Добро - 4
Есть - 5
Зело - 6
Земля - 7
Иже - 8
Фита - 9
И - 10
- тысячи
- тьма: х10 000
100 000 - легион
1000 000 - леодр
1050 - колода
. . .
= 10 000
"И более сего несть
человеческому уму разумевати".
Слайд 17 Коротко о главном
К НЕПОЗИЦИОННЫМ системам исчисления можно отнести системы
Римскую
Старославянскую
Вавилонскую
Древнеегипетскую
Китайскую
Ацтеков, майя …
НЕДОСТАТКИ:
Очень сложно выполнять математические расчеты
Необходимость большого числа различных знаков для записи чисел, особенно больших
Слайд 19Позиционной называют систему счисления, в которой число представляется в виде последовательности
3 3 3 3
1 позиция
* 1
2 позиция
* 10
3 позиция
* 100
4 позиция
* 1000
1000 100 10 1
(103) (102) (101) (100)
Базис позиционной системы счисления – это последовательность чисел, каждое из которых задает значение цифры «по месту» и «вес» каждого разряда.
Десятичная система: 1, 10, 102, 103, … , 10n
Двоичная система: 1, 2, 22, 23, … , 2n
P-ичная система: …, p-n, …, p-2, p-1, p0, p1 , … , pn
Слайд 20Позиционные системы счисления
Смешанные: p-q-ичные
Каждая цифра числа, заданного в p-ичной системе, заменяется
6548 10 = 0110 0101 0100 1000 2-10
1001 0010 0000 0111 2-10 = 9207 10
Слайд 21Позиционные системы счисления
Развернутая форма записи числа
Свернутая форма записи числа
А = anPn
Аp = an…a1a0, b-1…b-k...P
186,348
186,34810=1100+810+61+30,1+40,01+80,001=
=1102+8101+6100+310-1+410-2+810-3
Так можно представить любое число в 10-ичной СС…
231,445=252+351+150+45-1+45-2
…а также любое число в р-ичной системе счисления
Слайд 22Лейбниц (Leibniz) Готфрид Вильгельм
(1646-1716)
немецкий философ, математик, физик, языковед
Лейбниц, изрядное
Двоичная система счисления
С конца ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обрабатываемая ЭВМ, хранится в них в двоичном виде.
Лейбниц в 1697 г. разработал правила двоичной арифметики.
Он настолько был восхищен своим открытием, что в его честь
выпустил специальную медаль, на которой были даны двоичные
изображения начального ряда натуральных чисел — возможно,
это был тот редкий случай в истории математики, когда
математическое открытие было удостоено такой высокой почести.
Лейбниц, однако, не рекомендовал двоичную арифметику для
практических вычислений вместо десятичной системы, но
подчеркивал, что “вычисление с помощью двоек, то есть 0 и 1,
в вознаграждение его длиннот является для науки основным
и порождает новые открытия, которые оказываются полезными
впоследствии, даже в практике чисел, а особенно в геометрии:
причиной чего служит то обстоятельство, что при сведении чисел
к простейшим началам, каковы 0 и 1,
всюду выявляется чудесный порядок”.
Блестящие предсказания Лейбница сбылись только через два
с половиной столетия, когда выдающийся американский ученый,
физик и математик Джон фон Нейман предложил использовать
именно двоичную систему счисления в качестве универсального
способа кодирования информации в электронных компьютерах.