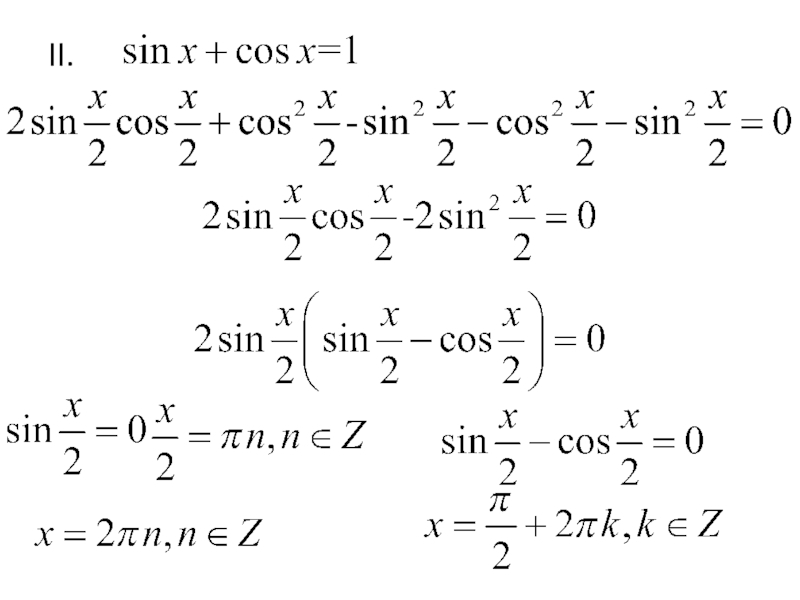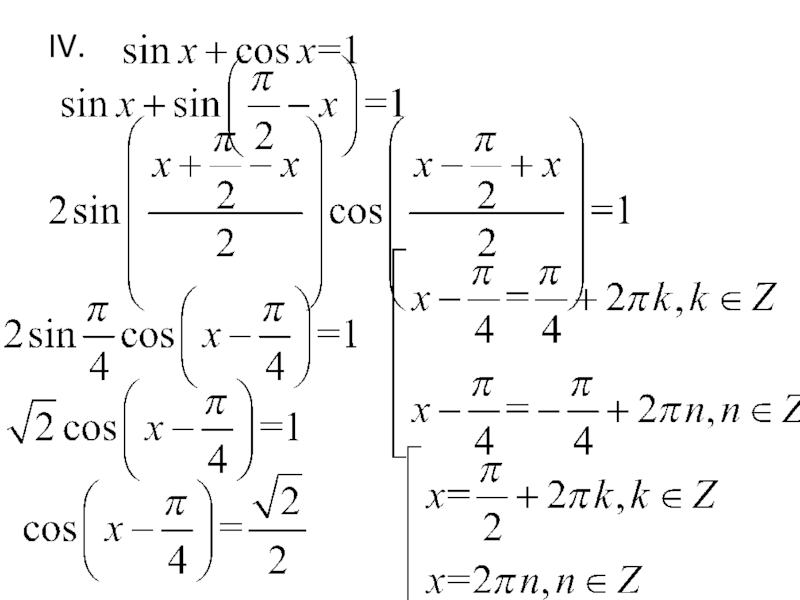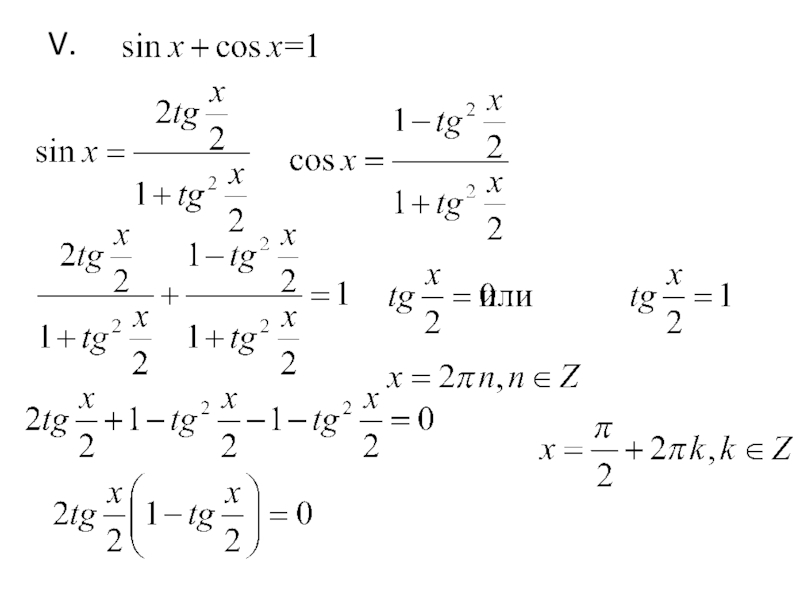- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад об учебно-исследовательской и проектной деятельности учащихся
Содержание
- 1. Презентация об учебно-исследовательской и проектной деятельности учащихся
- 2. ПО ЗАДАЧАМ
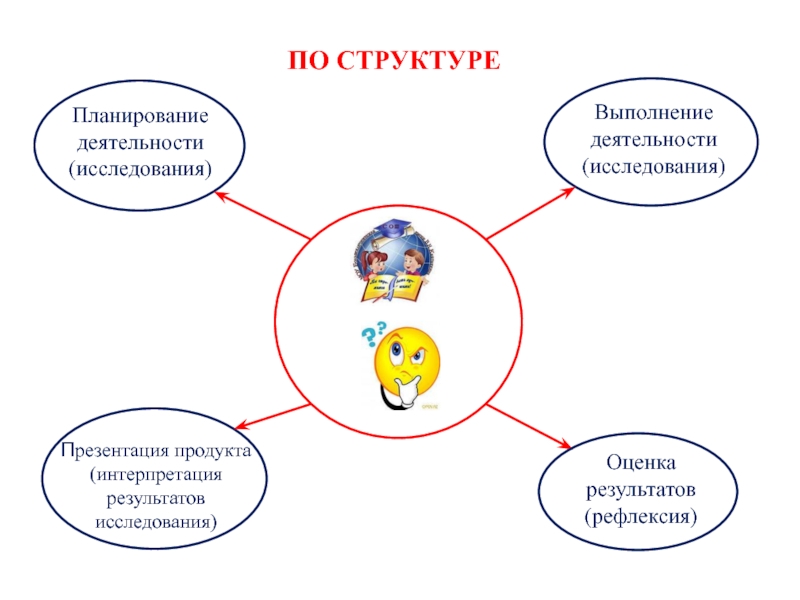
- 3. Планирование деятельности(исследования)Выполнение деятельности(исследования)Презентация продукта(интерпретация результатов исследования)Оценка результатов(рефлексия)ПО СТРУКТУРЕ
- 4. ПО РЕЗУЛЬТАТАМУчительученикиИнтеллектуальное, личностное RРост компетентности в выбранной
- 5. ПО ЗАДАЧАМ
- 6. ПО СТРУКТУРЕ
- 7. ПО РЕЗУЛЬТАТАМ
- 8. СТРУКТУРА ПРОЕКТНОЙ И УЧЕБНО-ИССЛЕДОВАТЕЛЬСКОЙ ДЕЯТЕЛЬНОСТИ
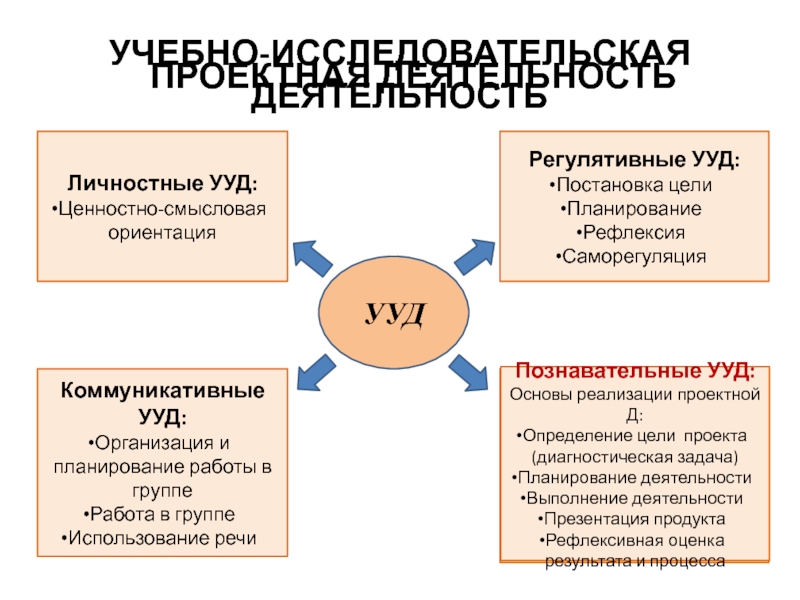
- 9. УЧЕБНО-ИССЛЕДОВАТЕЛЬСКАЯ ДЕЯТЕЛЬНОСТЬУУДЛичностные УУД:Ценностно-смысловая ориентацияРегулятивные УУД:Постановка целиПланированиеРефлексияСаморегуляцияКоммуникативные УУД:Организация
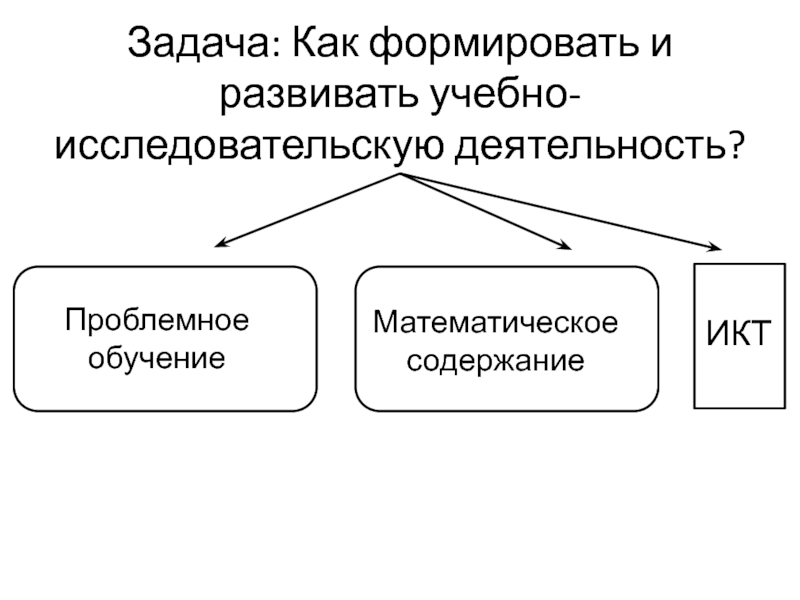
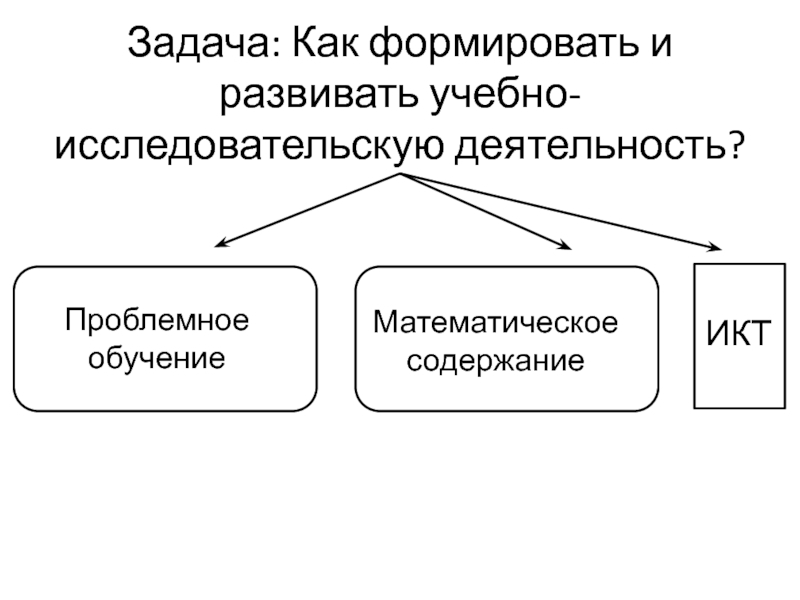
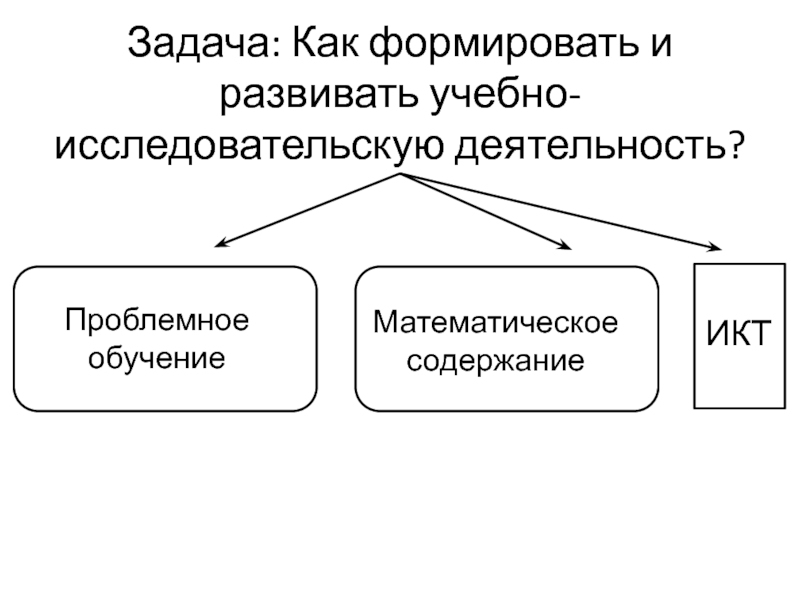
- 10. Задача: Как формировать и развивать учебно-исследовательскую деятельность?Проблемное обучениеМатематическоесодержаниеИКТ
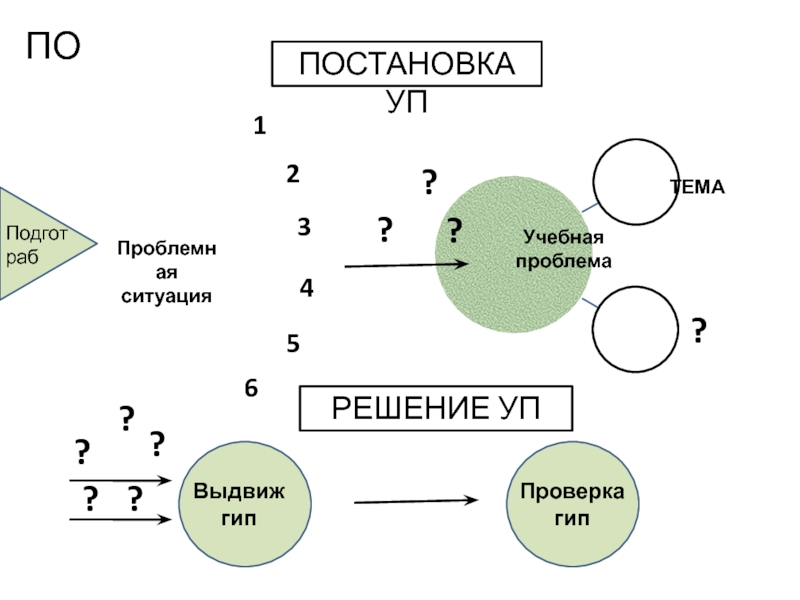
- 11. ПОСТАНОВКА УППроблемнаяситуация 123456Учебная проблемаТЕМА ?
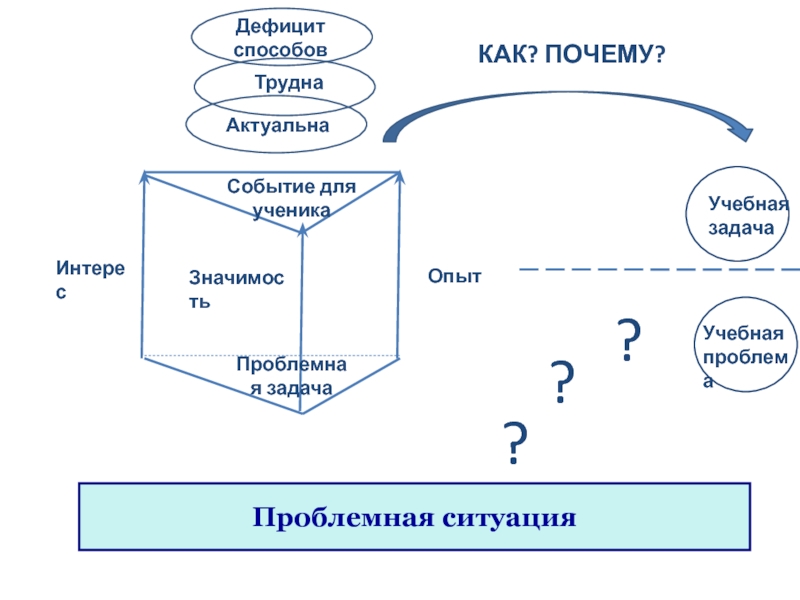
- 12. Проблемная ситуацияПроблемная задачаИнтересЗначимостьОпытСобытие для ученикаКАК? ПОЧЕМУ?АктуальнаТруднаДефицит способовУчебная задачаУчебная проблема???
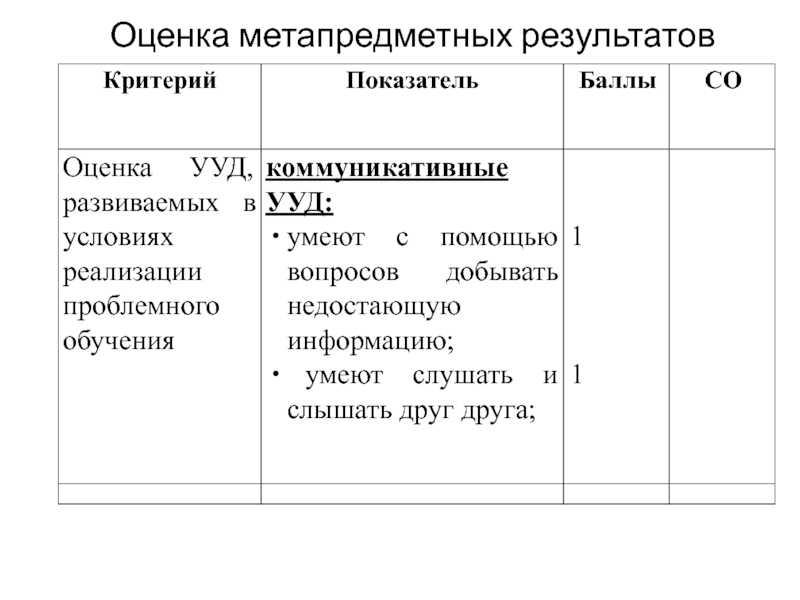
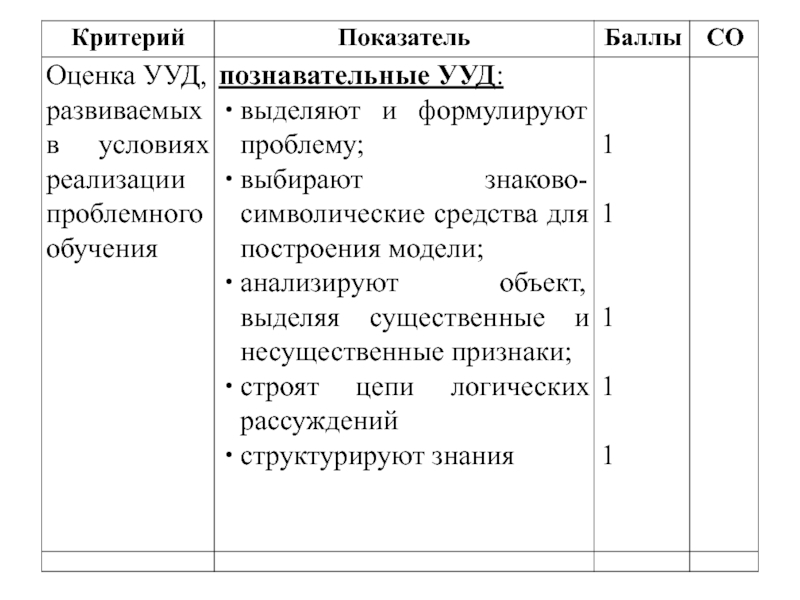
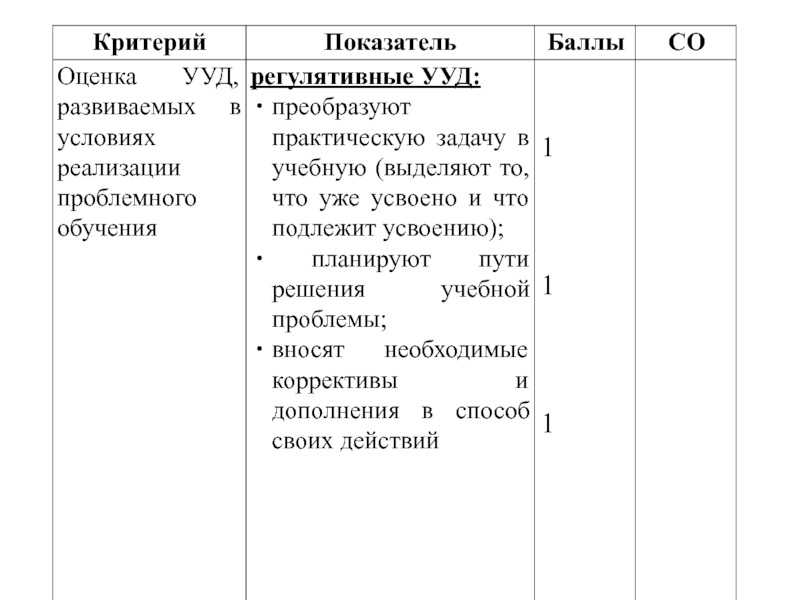
- 13. Оценка метапредметных результатов
- 14. Слайд 14
- 15. Слайд 15
- 16. Задача: Как формировать и развивать учебно-исследовательскую деятельность?Проблемное обучениеМатематическоесодержаниеИКТ
- 17. Учебно-исследовательская деятельность - специально-организованная познавательная творческая
- 18. Исследоват. умения
- 19. Учебно-исследовательскую деятельность учащихся целесообразно организовыватьпри:а) выявлении существенных
- 20. г) обобщении теоремы;д) составлении обратной теоремы и
- 21. з) классификации математических объектов, отношений между ними,
- 22. Задание 1. Решить уравнение различными способами:Познавательные УУД:Осуществлять
- 23. II.
- 24. III. Проверка
- 25. IV.
- 26. V.
- 27. ПроверимОтвет:Объяснять явления, процессы, связи и отношения, выявляемые в ходе исследования
- 28. !!!Проверим:Познавательные УУД:Осуществлять выбор наиболее рациональных способов решения задач в зависимости от конкретных условий
- 29. Задание 2: Построение котрпримеровКонтрпример – пример, опровергающий
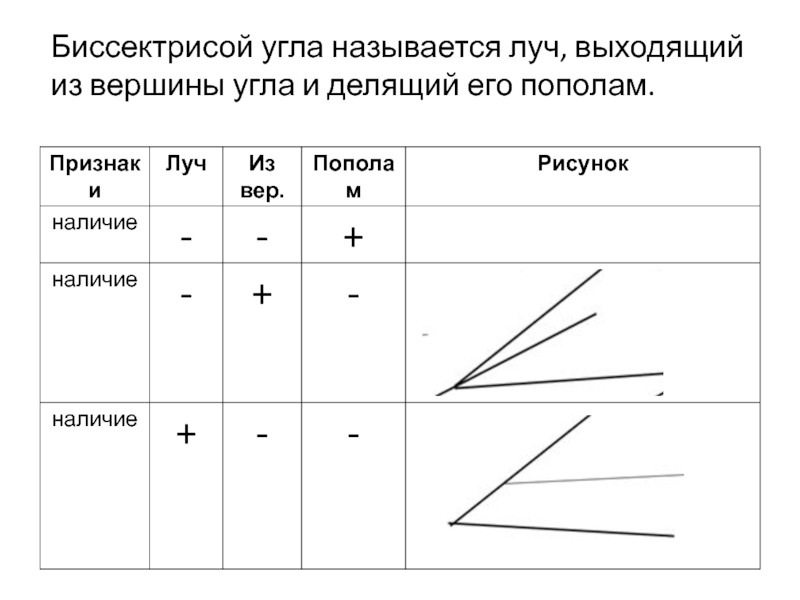
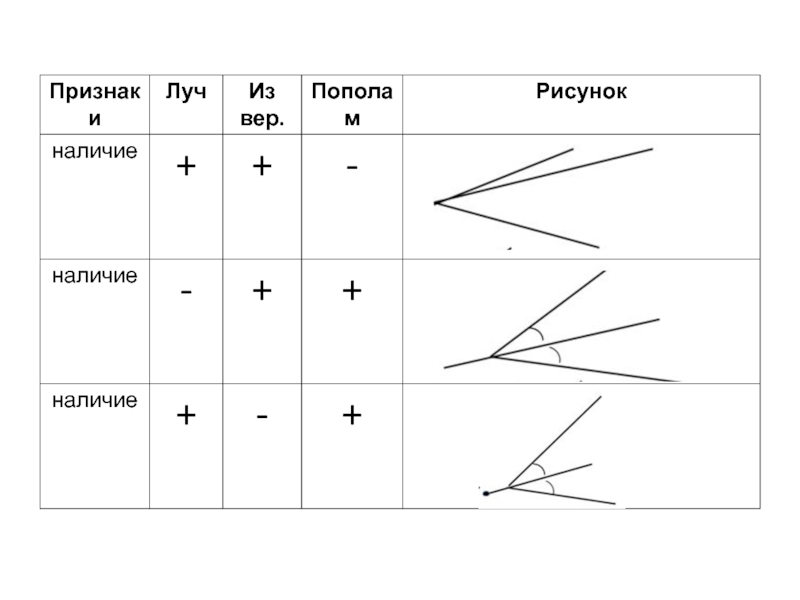
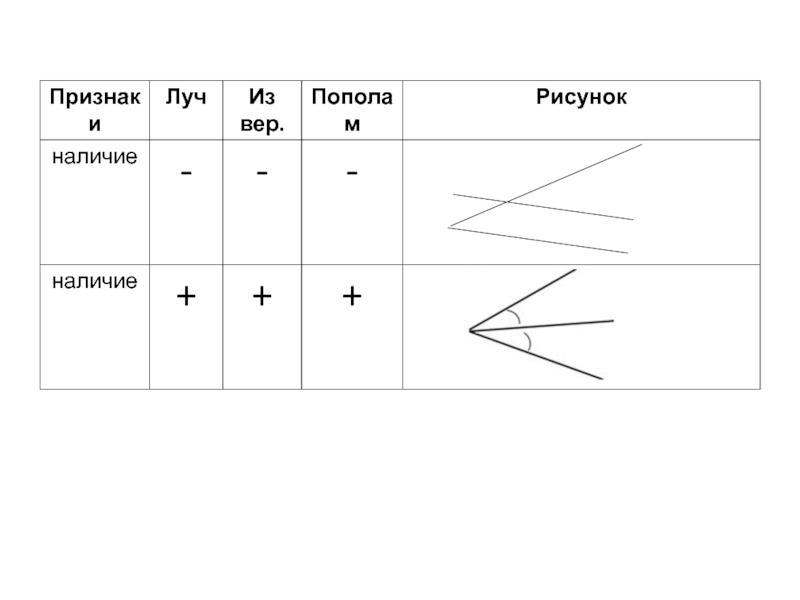
- 30. Биссектрисой угла называется луч, выходящий из вершины угла и делящий его пополам.
- 31. Слайд 31
- 32. Слайд 32
- 33. Задание 3. Выделение частных случаев некоторого факта в математике
- 34. Слайд 34
- 35. Нам надо решить задачу: при каких значениях
- 36. При каких значениях а уравнение имеет хотя
- 37. При каких значениях а уравнение имеет хотя
- 38. При каких значениях а уравнение имеет хотя
- 39. При каких значениях а уравнение имеет хотя
- 40. Задача: Как формировать и развивать учебно-исследовательскую деятельность?Проблемное обучениеМатематическоесодержаниеИКТ
- 41. Выполнение заданий в программе «Живая геометрия».Задание 1
- 42. Выполнение заданий в программе «Живая геометрия».Задание 2
ПО ЗАДАЧАМ
Слайд 3Планирование деятельности
(исследования)
Выполнение деятельности
(исследования)
Презентация продукта
(интерпретация результатов исследования)
Оценка результатов
(рефлексия)
ПО СТРУКТУРЕ
Слайд 4ПО РЕЗУЛЬТАТАМ
Учитель
ученики
Интеллектуальное, личностное R
Рост компетентности в выбранной сфере
Формирование умения сотрудничать
Работать самостоятельно
Освоение
основ исследовательской и проектной работы
Слайд 9УЧЕБНО-ИССЛЕДОВАТЕЛЬСКАЯ ДЕЯТЕЛЬНОСТЬ
УУД
Личностные УУД:
Ценностно-смысловая ориентация
Регулятивные УУД:
Постановка цели
Планирование
Рефлексия
Саморегуляция
Коммуникативные УУД:
Организация и планирование работы в
группе
Работа в группе
Использование речи
Работа в группе
Использование речи
Познавательные УУД:
Основы реализации У-И Д:
Осознание проблемы
Выдвижение гипотез
Планирование
Осуществление исследования
Получение результатов
Оценка и интерпретация результатов
ПРОЕКТНАЯ ДЕЯТЕЛЬНОСТЬ
Познавательные УУД:
Основы реализации проектной Д:
Определение цели проекта (диагностическая задача)
Планирование деятельности
Выполнение деятельности
Презентация продукта
Рефлексивная оценка результата и процесса
Слайд 10Задача: Как формировать и развивать учебно-исследовательскую деятельность?
Проблемное обучение
Математическое
содержание
ИКТ
Слайд 11ПОСТАНОВКА УП
Проблемная
ситуация
1
2
3
4
5
6
Учебная проблема
ТЕМА
?
?
?
?
ПО
РЕШЕНИЕ УП
Выдвиж
гип
?
?
?
?
?
Проверка
гип
Подгот раб
Слайд 12Проблемная ситуация
Проблемная задача
Интерес
Значимость
Опыт
Событие для ученика
КАК? ПОЧЕМУ?
Актуальна
Трудна
Дефицит способов
Учебная задача
Учебная проблема
?
?
?
Слайд 16Задача: Как формировать и развивать учебно-исследовательскую деятельность?
Проблемное обучение
Математическое
содержание
ИКТ
Слайд 17Учебно-исследовательская деятельность -
специально-организованная познавательная творческая деятельность учащихся, в
процессе осуществления которой происходит поиск и открытие знаний.
Слайд 19Учебно-исследовательскую деятельность учащихся целесообразно организовывать
при:
а) выявлении существенных свойств понятий или отношений
между ними;
б) установлении связей данного понятия с другими;
в) ознакомлении с фактом, отраженном в формулировке теоремы, в доказательстве
теоремы;
б) установлении связей данного понятия с другими;
в) ознакомлении с фактом, отраженном в формулировке теоремы, в доказательстве
теоремы;
Слайд 20г) обобщении теоремы;
д) составлении обратной теоремы и проверке ее истинности;
е) выделении
частных случаев некоторого факта в математике;
ж) обобщении различных вопросов;
ж) обобщении различных вопросов;
Слайд 21з) классификации математических объектов, отношений между ними, основных фактов данного раздела
математики;
и) решении задач различными способами;
к) составлении новых задач, вытекающих из решения данных;
л) построении контрпримеров и т.д.
и) решении задач различными способами;
к) составлении новых задач, вытекающих из решения данных;
л) построении контрпримеров и т.д.
Слайд 22Задание 1. Решить уравнение различными способами:
Познавательные УУД:
Осуществлять выбор наиболее рациональных способов
решения задач в зависимости от конкретных условий
Слайд 27Проверим
Ответ:
Объяснять явления, процессы, связи и отношения, выявляемые в ходе исследования
Слайд 28!!!
Проверим:
Познавательные УУД:
Осуществлять выбор наиболее рациональных способов решения задач в зависимости от
конкретных условий
Слайд 29Задание 2: Построение котрпримеров
Контрпример – пример, опровергающий верность некоторого утверждения.
Построение контрпримера
– классический способ опровержения гипотез.
Приводить контпримеры – строить отрицание определений различных конструкций.
Приводить контпримеры – строить отрицание определений различных конструкций.
Слайд 35Нам надо решить задачу: при каких значениях а квадратное уравнение имеет
хотя бы один положительный корень?
Для того, чтобы квадратное уравнение имело хотя бы один корень, необходимо D≥0:
при любых а.
Познавательные УУД:
преобразование модели для решения задачи
Слайд 36При каких значениях а уравнение
имеет хотя бы один положительный корень?
Возможны
три случая:
1) равные и положительные;
2) неравные и положительные;
3) неравные, один из которых положительный.
Познавательные УУД:
создание схемы для решения задачи
Слайд 37При каких значениях а уравнение
имеет хотя бы один положительный корень?
Случай
1: равные и положительные корни.
нет решений.
Познавательные УУД:
создание модели
Слайд 38При каких значениях а уравнение
имеет хотя бы один положительный корень?
Случай
2: неравные и положительные корни (по теореме Виета).
нет решений.
Познавательные УУД:
создание модели
Слайд 39При каких значениях а уравнение
имеет хотя бы один положительный корень?
Случай
3: неравные корни, один из которых положительный (по теореме Виета).
a < 0
Ответ: a < 0
Познавательные УУД:
создание модели
Слайд 40Задача: Как формировать и развивать учебно-исследовательскую деятельность?
Проблемное обучение
Математическое
содержание
ИКТ
Слайд 41Выполнение заданий в программе «Живая геометрия».
Задание 1 (тема: «Четыре замечательные точки
треугольника»)
Постройте серединные перпендикуляры к сторонам треугольника. Ответьте на вопрос: что можно сказать о пересечении серединных перпендикуляров?
Постройте серединные перпендикуляры к сторонам треугольника. Ответьте на вопрос: что можно сказать о пересечении серединных перпендикуляров?
Познавательные УУД:
объяснять связи и отношения, выявляемые в ходе исследования;
Слайд 42Выполнение заданий в программе «Живая геометрия».
Задание 2 (тема: «Вписанная и описанная
окружности»)
Провести исследовательскую работу относительно центра описанной окружности около треугольников разных видов.
Провести исследовательскую работу относительно центра описанной окружности около треугольников разных видов.
Познавательные УУД:
осуществлять сравнение, выбирая основания
