- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Преобразование фигур на плоскости
Содержание
- 1. Презентация по математике на тему Преобразование фигур на плоскости
- 2. Преобразование фигур на плоскости
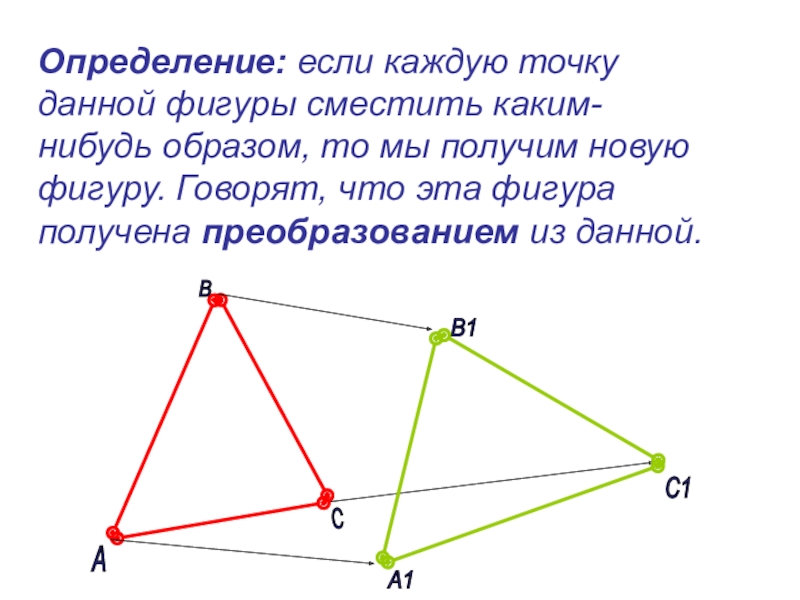
- 3. Определение: если каждую точку данной
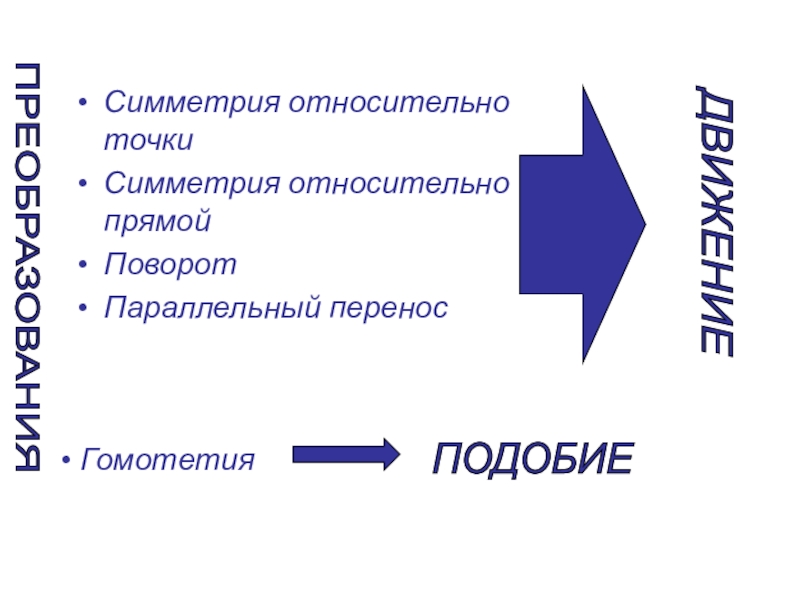
- 4. Симметрия относительно точкиСимметрия относительно прямойПоворотПараллельный перенос ПРЕОБРАЗОВАНИЯ ДВИЖЕНИЕ ПОДОБИЕ Гомотетия
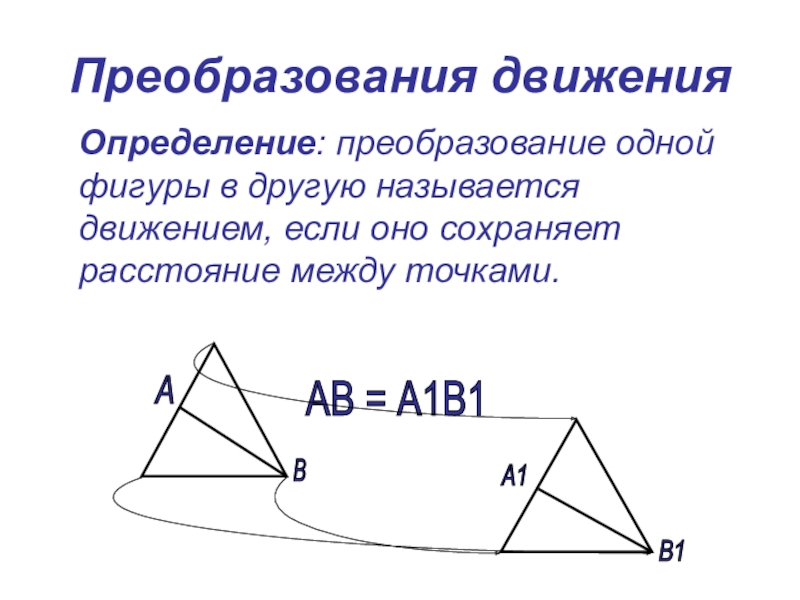
- 5. Преобразования движения Определение: преобразование одной фигуры
- 6. Свойства движенияДва движения, выполненные последовательно, дают снова
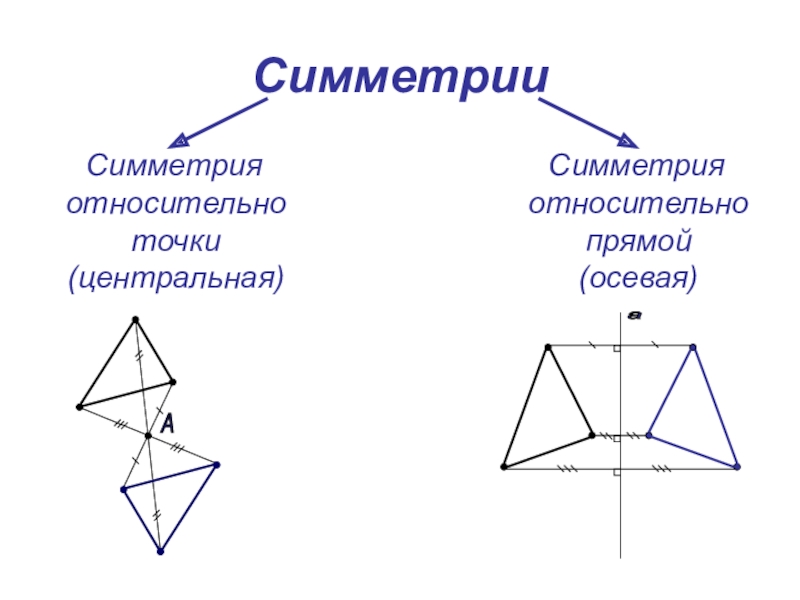
- 7. Симметрии Симметрия относительно точки (центральная) Симметрия относительно прямой (осевая)А а
- 8. Симметрия относительно точкиЦентральная симметрия является движениемДоказательство: Рассмотрим
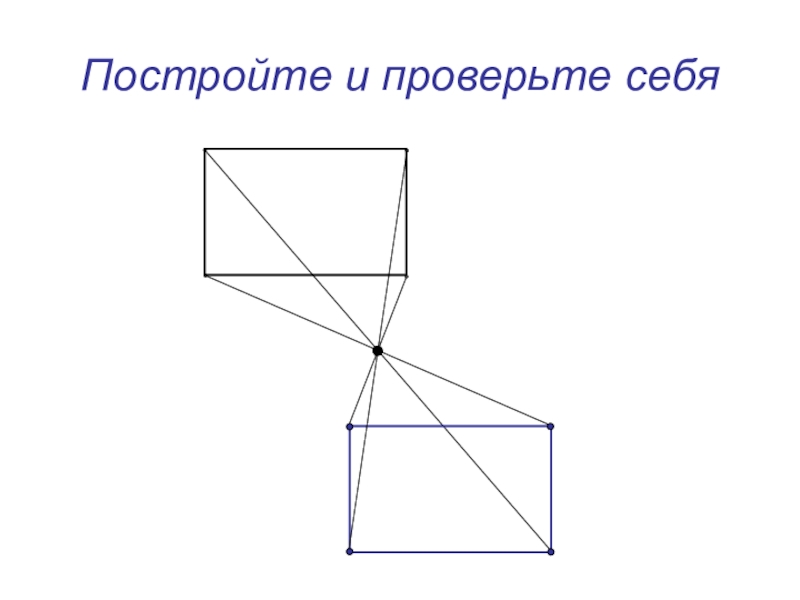
- 9. Постройте и проверьте себя
- 10. Центрально-симметричные фигуры Определение: фигура называется
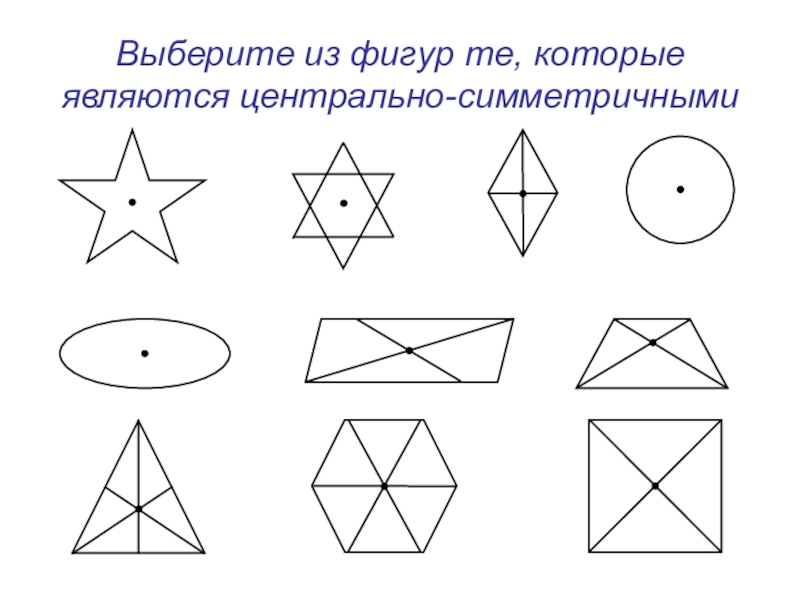
- 11. Выберите из фигур те, которые являются центрально-симметричными
- 12. 1. Укажите координаты точки,
- 13. 2. В координатной плоскости даны
- 14. 3. Начертите треугольник АВС. Постройте
- 15. 4. Даны угол АВС и
- 16. 5. Даны пересекающиеся прямые и
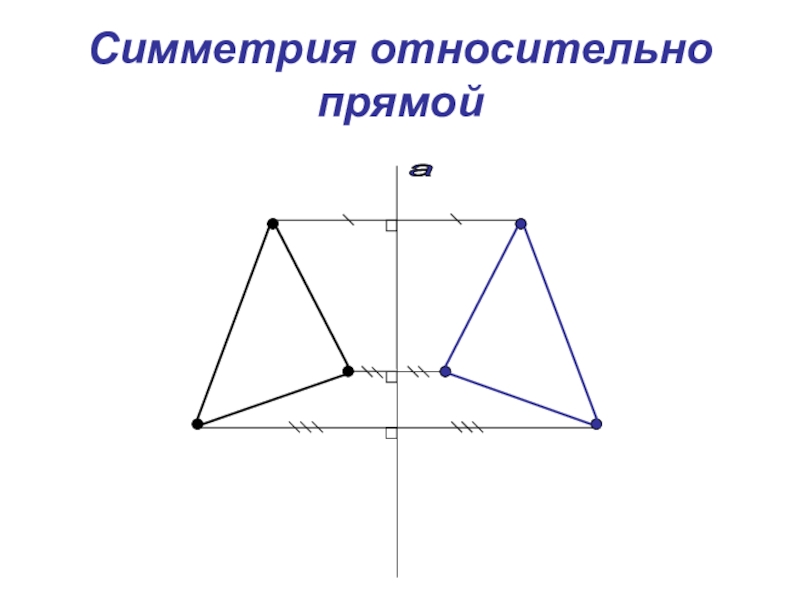
- 17. Симметрия относительно прямойа
- 18. Симметрия относительно прямой является движением Доказательство:
- 19. Определение: если преобразование симметрии относительно
- 20. Какие из этих фигур имеют ось симметрии?
- 21. Решите задачи 1.В координатной плоскости даны
- 22. 2.В координатной плоскости даны точки
- 23. 3. Начертите треугольник АВС. Постройте
- 24. Симметрия в природе
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
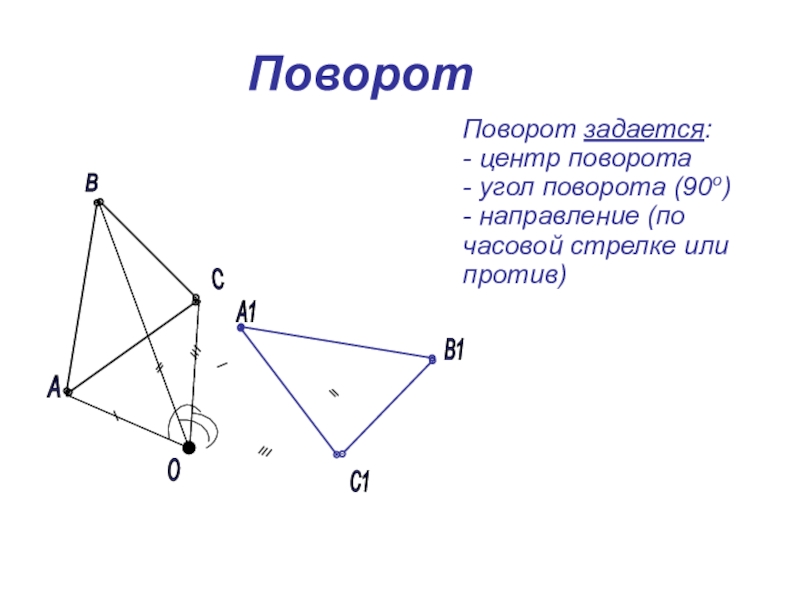
- 29. Поворот Поворот задается: - центр поворота
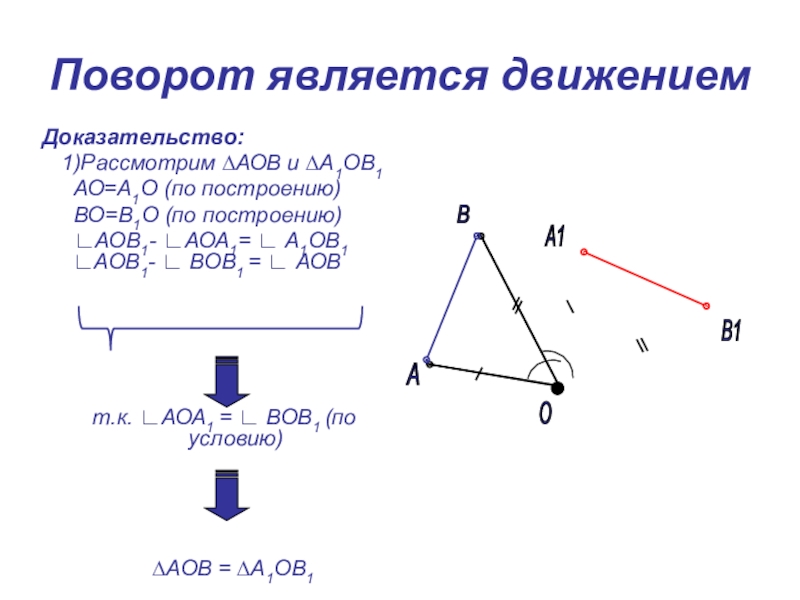
- 30. Поворот является движениемДоказательство: 1)Рассмотрим ∆АОВ и
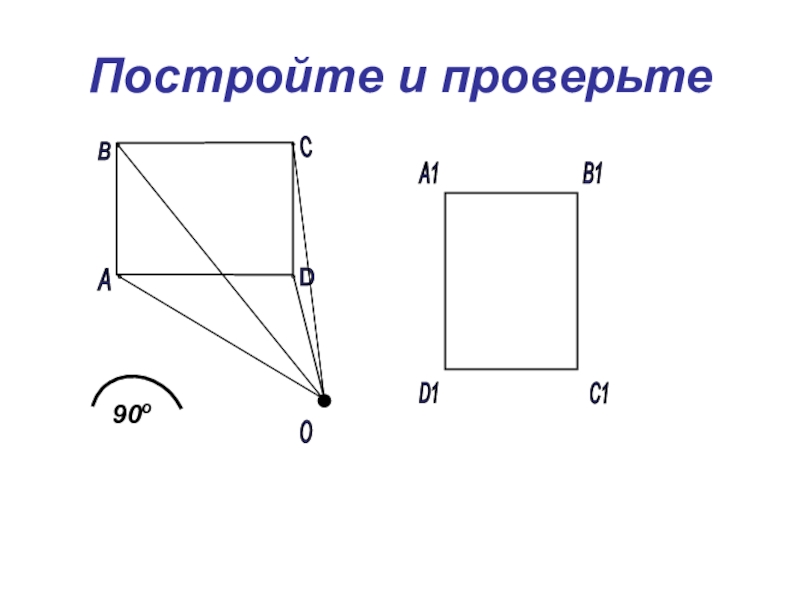
- 31. В1 С1 D1 А1 D Постройте и проверьте А В С О 90о
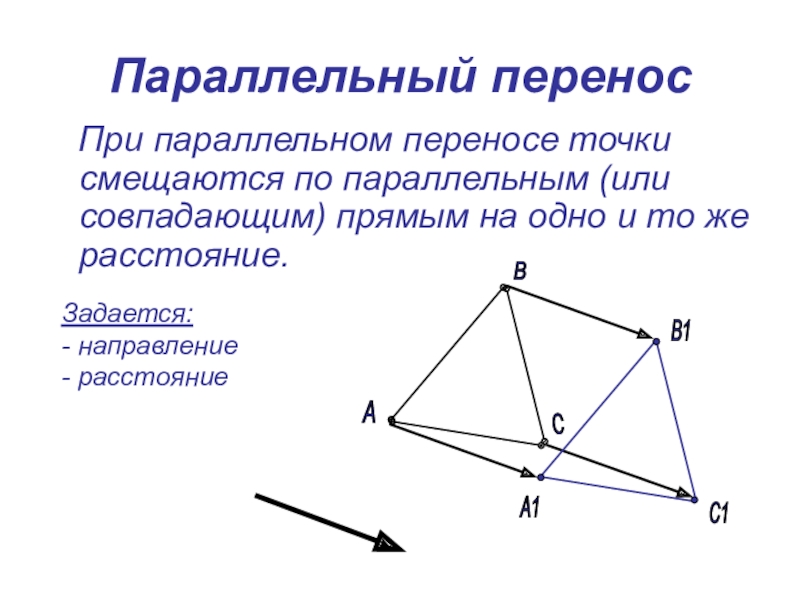
- 32. Параллельный перенос При параллельном переносе точки
- 33. Параллельный перенос является движениемДоказательство: Рассмотрим
- 34. Свойства параллельного переносаПри параллельном переносе прямая переходит
- 35. Параллельный перенос в координатах Введем на
- 36. Формулы параллельного переносаПример: А(3;-2) переходит в точку
- 37. Дано: параллельный перенос С С` В
- 38. 2. Точка А(7;9) при параллельном переносе переходит
- 39. 3. При параллельном переносе точка А(1;-6)
- 40. Успешного вам выполнения контрольной работы по теме: «Преобразования фигур на плоскости»
Преобразование фигур на плоскости
Слайд 3 Определение: если каждую точку данной фигуры сместить каким-нибудь образом,
то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.
А
В
С
А1
В1
С1
Слайд 4Симметрия относительно
точки
Симметрия относительно
прямой
Поворот
Параллельный перенос
ПРЕОБРАЗОВАНИЯ
ДВИЖЕНИЕ
ПОДОБИЕ
Гомотетия
Слайд 5Преобразования движения
Определение: преобразование одной фигуры в другую называется движением,
если оно сохраняет расстояние между точками.
А
А1
В
В1
АВ = А1В1
Слайд 6Свойства движения
Два движения, выполненные последовательно, дают снова движение.
Преобразование, обратное движению, также
является движением.
Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
При движении прямые переходят в прямые, полупрямые - в полупрямые, отрезки - в отрезки.
При движении сохраняются углы.
Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.
При движении прямые переходят в прямые, полупрямые - в полупрямые, отрезки - в отрезки.
При движении сохраняются углы.
Слайд 7Симметрии
Симметрия относительно точки
(центральная)
Симметрия относительно прямой
(осевая)
А
а
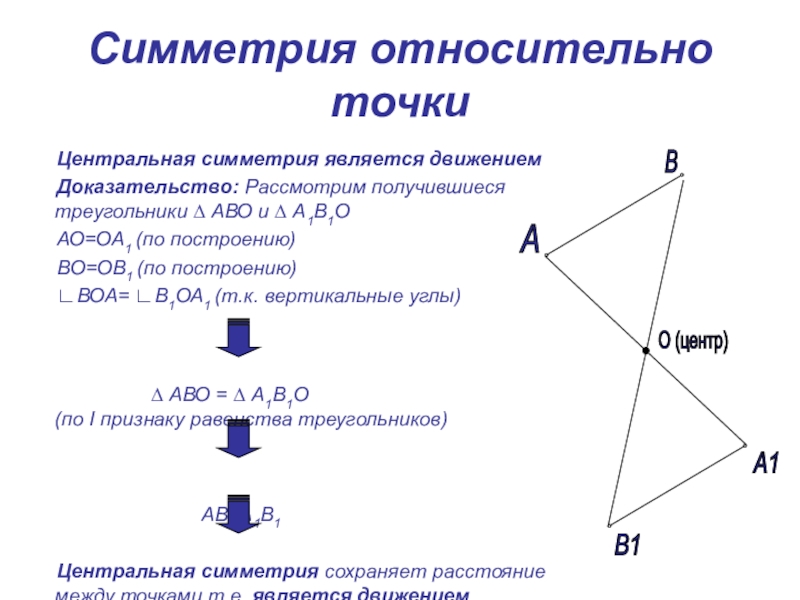
Слайд 8Симметрия относительно точки
Центральная симметрия является движением
Доказательство: Рассмотрим получившиеся треугольники ∆
АВО и ∆ А1В1О
АО=ОА1 (по построению)
ВО=ОВ1 (по построению)
∟ВОА= ∟В1ОА1 (т.к. вертикальные углы)
∆ АВО = ∆ А1В1О (по Ι признаку равенства треугольников)
АВ=А1В1
Центральная симметрия сохраняет расстояние между точками т.е. является движением
АО=ОА1 (по построению)
ВО=ОВ1 (по построению)
∟ВОА= ∟В1ОА1 (т.к. вертикальные углы)
∆ АВО = ∆ А1В1О (по Ι признаку равенства треугольников)
АВ=А1В1
Центральная симметрия сохраняет расстояние между точками т.е. является движением
А
В
А1
В1
О (центр)
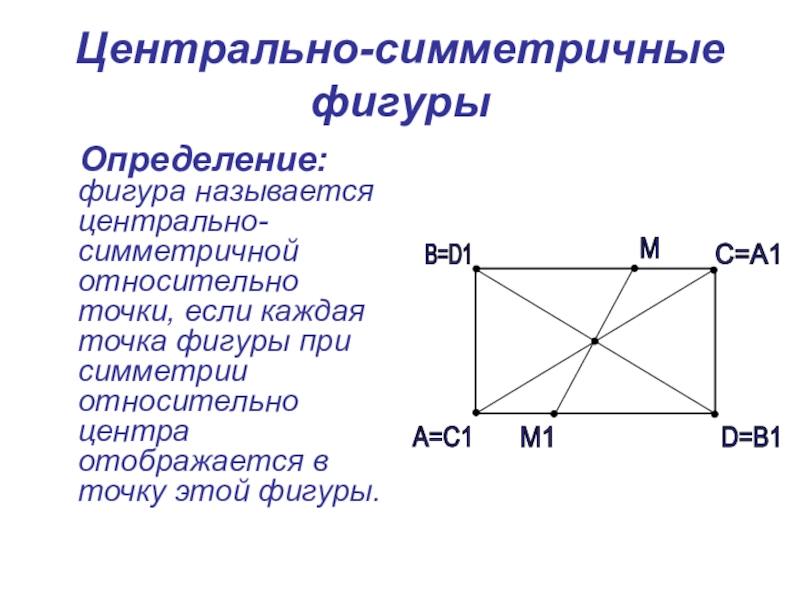
Слайд 10Центрально-симметричные фигуры
Определение: фигура называется центрально-симметричной относительно точки, если
каждая точка фигуры при симметрии относительно центра отображается в точку этой фигуры.
В=D1
М
М1
А=С1
С=А1
D=В1
Слайд 12 1. Укажите координаты точки, симметричные точке А(-5;-3) относительно
начала координат.
Ответ: А1(5;3)
Ответ: А1(5;3)
Решите задачи
Слайд 13 2. В координатной плоскости даны точки А(0;6), В(2;3), С(-5;0),
D(-1;-5), F(4;-1). Укажите их координаты, симметричные данным точкам относительно начала координат.
Ответ: А1(о;-6), В1 (-2;-3), С1 (5;0), D1 (1;5), F1 (-4;1).
Ответ: А1(о;-6), В1 (-2;-3), С1 (5;0), D1 (1;5), F1 (-4;1).
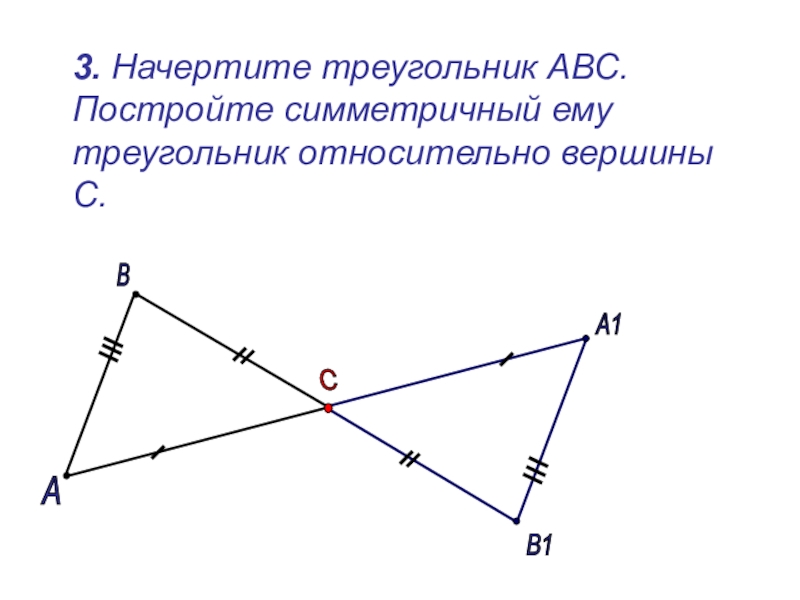
Слайд 14 3. Начертите треугольник АВС. Постройте симметричный ему треугольник относительно
вершины С.
А
В
С
А1
В1
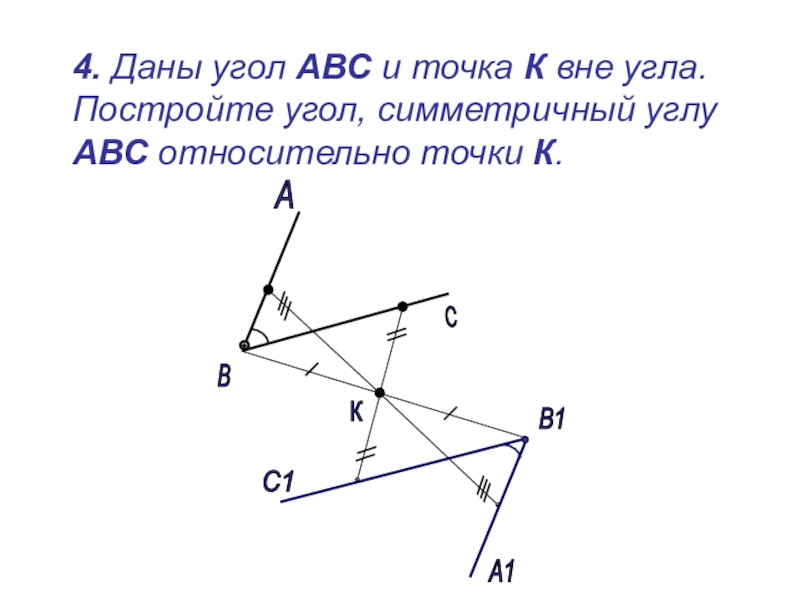
Слайд 15 4. Даны угол АВС и точка К вне угла.
Постройте угол, симметричный углу АВС относительно точки К.
А
В
С
К
В1
А1
С1
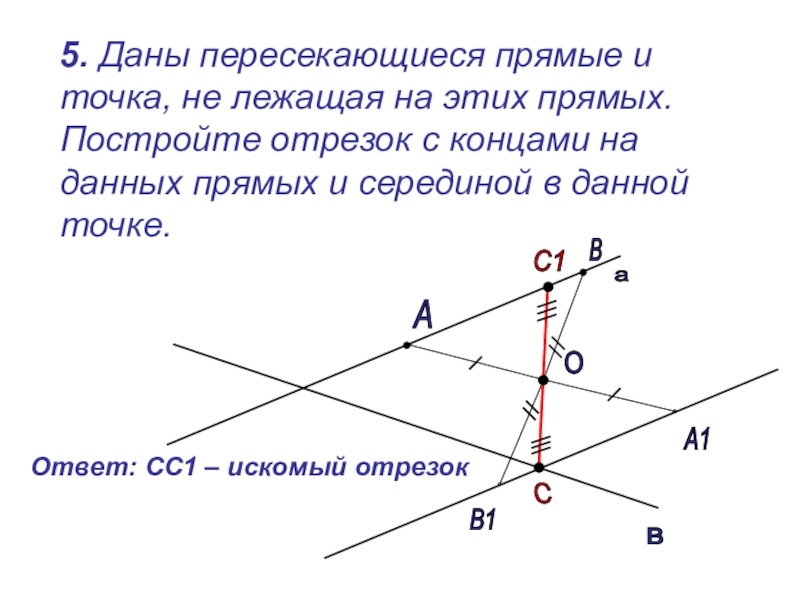
Слайд 16 5. Даны пересекающиеся прямые и точка, не лежащая на
этих прямых. Постройте отрезок с концами на данных прямых и серединой в данной точке.
Ответ: СС1 – искомый отрезок
Ответ: СС1 – искомый отрезок
В
а
в
О
А
В1
А1
С
С1
Слайд 18
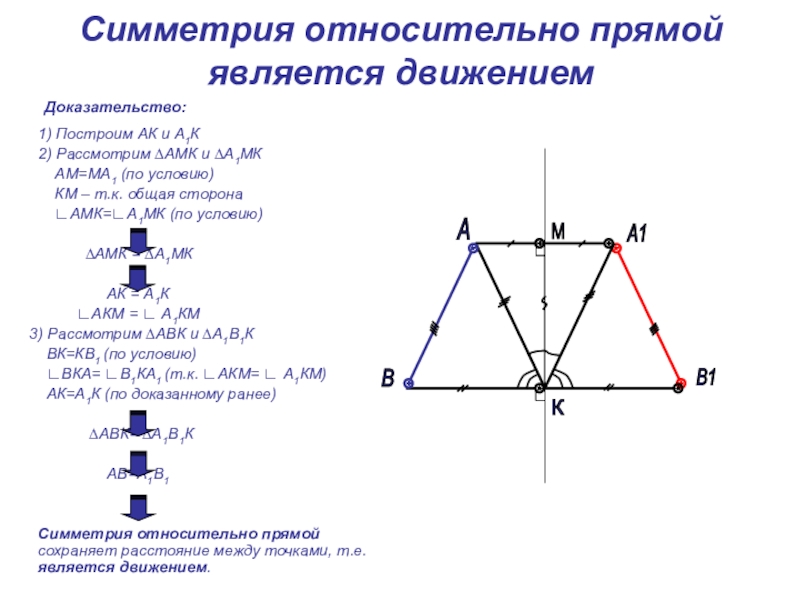
Симметрия относительно прямой является движением
Доказательство:
1) Построим АК и А1К
2) Рассмотрим ∆АМК и ∆А1МК
АМ=МА1 (по условию)
КМ – т.к. общая сторона
∟АМК=∟А1МК (по условию)
∆АМК = ∆А1МК
АК = А1К
∟АКМ = ∟ А1КМ
3) Рассмотрим ∆АВК и ∆А1В1К
ВК=КВ1 (по условию)
∟ВКА= ∟В1КА1 (т.к. ∟АКМ= ∟ А1КМ)
АК=А1К (по доказанному ранее)
∆АВК= ∆А1В1К
АВ=А1В1
Симметрия относительно прямой сохраняет расстояние между точками, т.е. является движением.
2) Рассмотрим ∆АМК и ∆А1МК
АМ=МА1 (по условию)
КМ – т.к. общая сторона
∟АМК=∟А1МК (по условию)
∆АМК = ∆А1МК
АК = А1К
∟АКМ = ∟ А1КМ
3) Рассмотрим ∆АВК и ∆А1В1К
ВК=КВ1 (по условию)
∟ВКА= ∟В1КА1 (т.к. ∟АКМ= ∟ А1КМ)
АК=А1К (по доказанному ранее)
∆АВК= ∆А1В1К
АВ=А1В1
Симметрия относительно прямой сохраняет расстояние между точками, т.е. является движением.
А
В
А1
В1
К
М
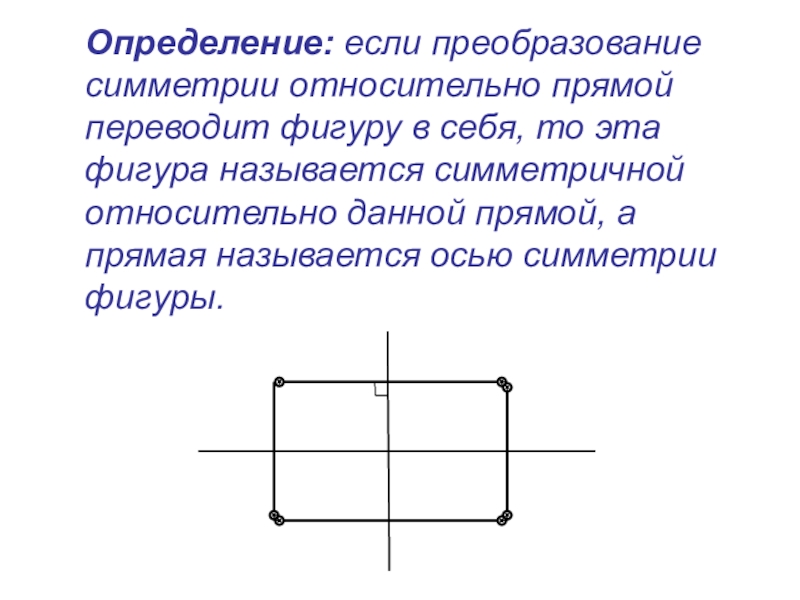
Слайд 19 Определение: если преобразование симметрии относительно прямой переводит фигуру в
себя, то эта фигура называется симметричной относительно данной прямой, а прямая называется осью симметрии фигуры.
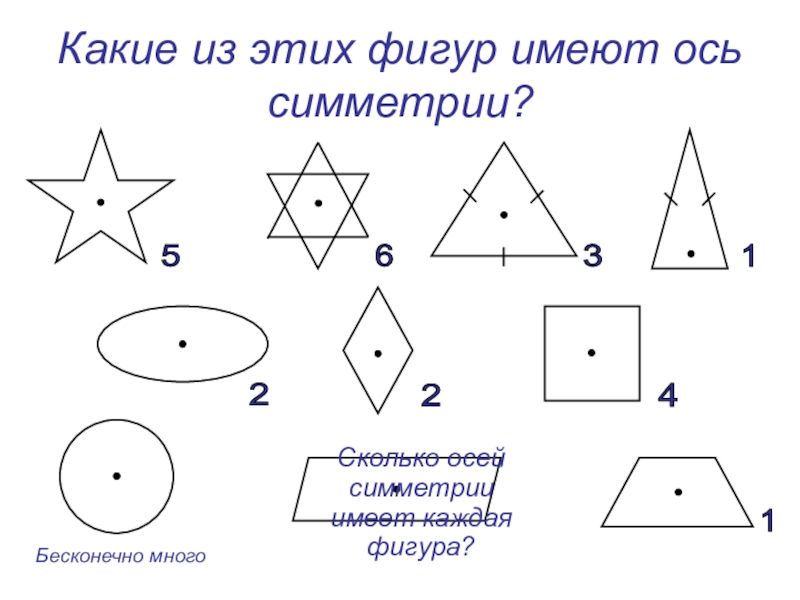
Слайд 20Какие из этих фигур имеют ось симметрии?
Сколько осей симметрии
имеет каждая фигура?
5
6
3
1
1
2
2
4
Бесконечно много
Слайд 21Решите задачи
1.В координатной плоскости даны точки А(0;6), В(2;3), С(-5;0),
D(-1;-5), F(4;-1). Укажите их координаты, симметричные данным точкам относительно оси Оx.
Ответ: А1 (0;-6), В1 (2;-3), С1 (-5;0), D1 (-1;5), F1 (4;1).
Ответ: А1 (0;-6), В1 (2;-3), С1 (-5;0), D1 (-1;5), F1 (4;1).
Слайд 22 2.В координатной плоскости даны точки А(0;6), В(2;3), С(-5;0), D(-1;-5),
F(4;-1). Укажите их координаты, симметричные данным точкам относительно оси Оy.
Ответ: А1 (0;6) , В1 (-2;3) , С1 (5;0) , D1 (1;-5) , F1 (-4;1) .
Ответ: А1 (0;6) , В1 (-2;3) , С1 (5;0) , D1 (1;-5) , F1 (-4;1) .
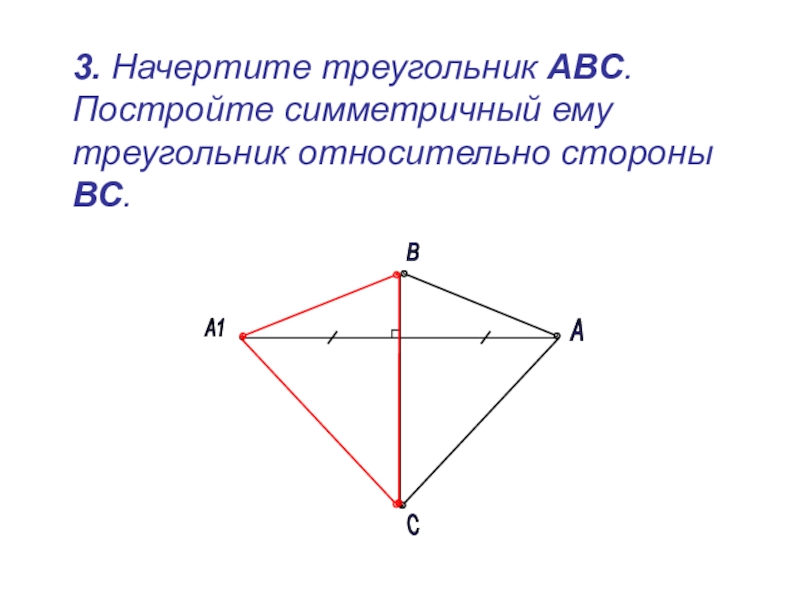
Слайд 23 3. Начертите треугольник АВС. Постройте симметричный ему треугольник относительно
стороны ВС.
А
В
А1
С
Слайд 29Поворот
Поворот задается:
- центр поворота
- угол поворота (90о)
- направление
(по часовой стрелке или против)
А
В
С
О
А1
В1
С1
Слайд 30Поворот является движением
Доказательство:
1)Рассмотрим ∆АОВ и ∆А1ОВ1
АО=А1О
(по построению)
ВО=В1О (по построению)
∟АОВ1- ∟АОА1= ∟ А1ОВ1 ∟АОВ1- ∟ ВОВ1 = ∟ АОВ
т.к. ∟АОА1 = ∟ ВОВ1 (по условию)
∆АОВ = ∆А1ОВ1
ВО=В1О (по построению)
∟АОВ1- ∟АОА1= ∟ А1ОВ1 ∟АОВ1- ∟ ВОВ1 = ∟ АОВ
т.к. ∟АОА1 = ∟ ВОВ1 (по условию)
∆АОВ = ∆А1ОВ1
А
В
А1
В1
О
Слайд 32Параллельный перенос
При параллельном переносе точки смещаются по параллельным (или
совпадающим) прямым на одно и то же расстояние.
Задается:
- направление
- расстояние
А
В
С
А1
В1
С1
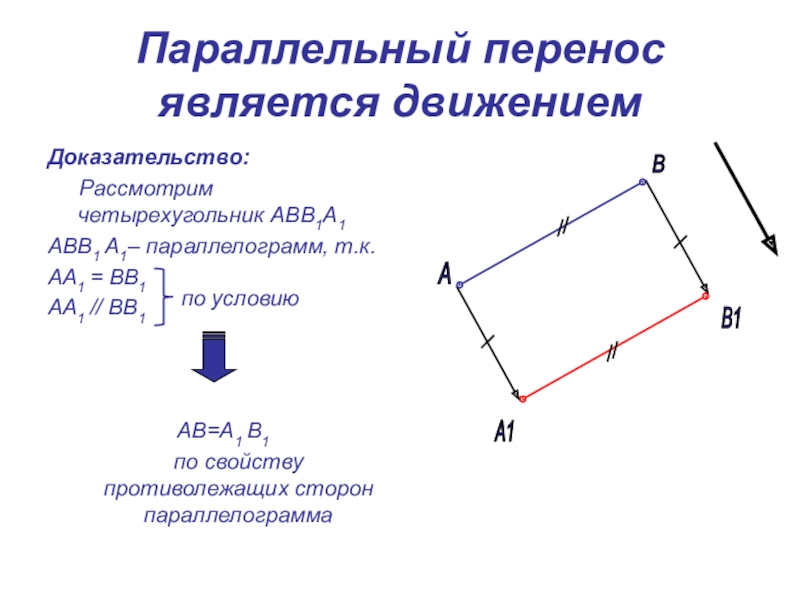
Слайд 33Параллельный перенос является движением
Доказательство:
Рассмотрим
четырехугольник АВВ1А1
АВВ1 А1– параллелограмм, т.к.
АА1 = ВВ1
АА1 // ВВ1
АВ=А1 В1
по свойству противолежащих сторон параллелограмма
по условию
А
В
А1
В1
Слайд 34Свойства параллельного переноса
При параллельном переносе прямая переходит в параллельную прямую (или
в себя).
2) Каковы бы ни были две точки А и А1 существует один и только один параллельный перенос, при котором точка А переходит в точку А1.
2) Каковы бы ни были две точки А и А1 существует один и только один параллельный перенос, при котором точка А переходит в точку А1.
Слайд 35Параллельный перенос в координатах
Введем на плоскости декартовы координаты x,
y. Преобразование фигуры F, при котором произвольная ее точка (x; y) переходит в точку
(x + a; y + b), где a и b – одни и те же для всех точек (x; y), называется параллельным переносом. Параллельный перенос задается формулами
x` = x + a, y` = y + b
Эти формулы выражают координаты x`, y` точки, в которую переходит точка (x; y) при параллельном переносе.
x` = x + a, y` = y + b
Эти формулы выражают координаты x`, y` точки, в которую переходит точка (x; y) при параллельном переносе.
Слайд 36Формулы параллельного переноса
Пример: А(3;-2) переходит в точку А` Найдите координаты точки
А`, если а=5, b=4.
Решение:
x` = 3+5, y` = -2+4
Ответ: А`(8;2)
Решение:
x` = 3+5, y` = -2+4
Ответ: А`(8;2)
x` = x + a, y` = y + b
Слайд 37Дано: параллельный перенос С С` В В`, а=3, b=1; С(-2;7),
В(6;4).
Найти: В`-? С`-?
Ответ: В`(9;5), С`(1;8)
Ответ: В`(9;5), С`(1;8)
Решение задач
Слайд 382. Точка А(7;9) при параллельном переносе переходит в точку А`(4;11). Найти:
а-?, b-?
Ответ: а=-3, b=2
Ответ: а=-3, b=2
Слайд 393. При параллельном переносе точка А(1;-6) переходит в точку А`(5;2). В
какую точку при этом же параллельном переносе перейдет точка В(-3;4)?
Ответ: В`(1;12)
Ответ: В`(1;12)
