- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Комбинаторика
Содержание
- 1. Презентация по математике Комбинаторика
- 2. ОпределениеКомбинаторика - это раздел математики, в котором
- 3. Из истории комбинаторикиКомбинаторика занимается различного вида соединениями,
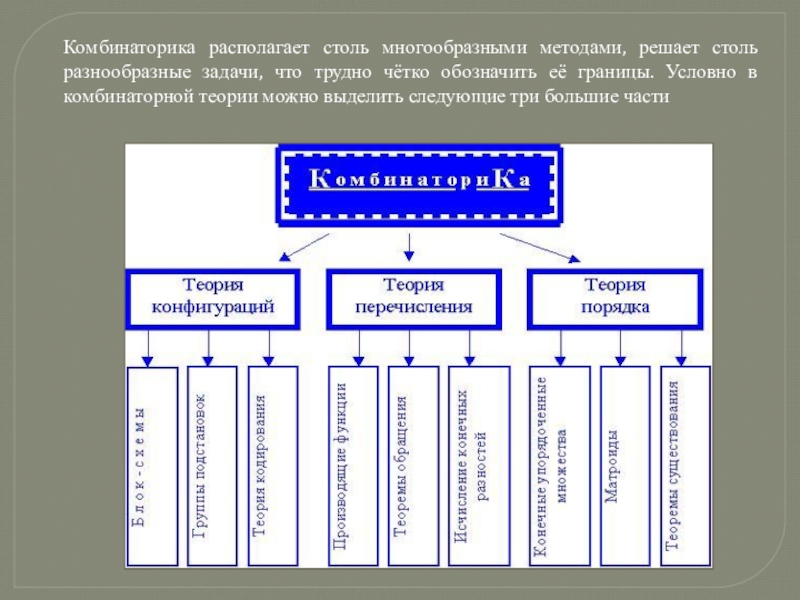
- 4. Комбинаторика располагает столь многообразными методами, решает столь
- 5. Комбинаторика — важный раздел математики, знание которого
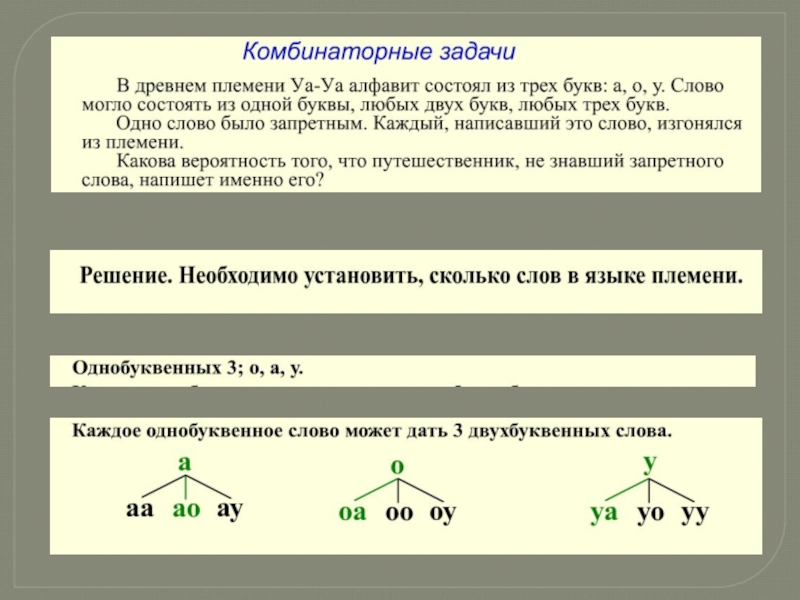
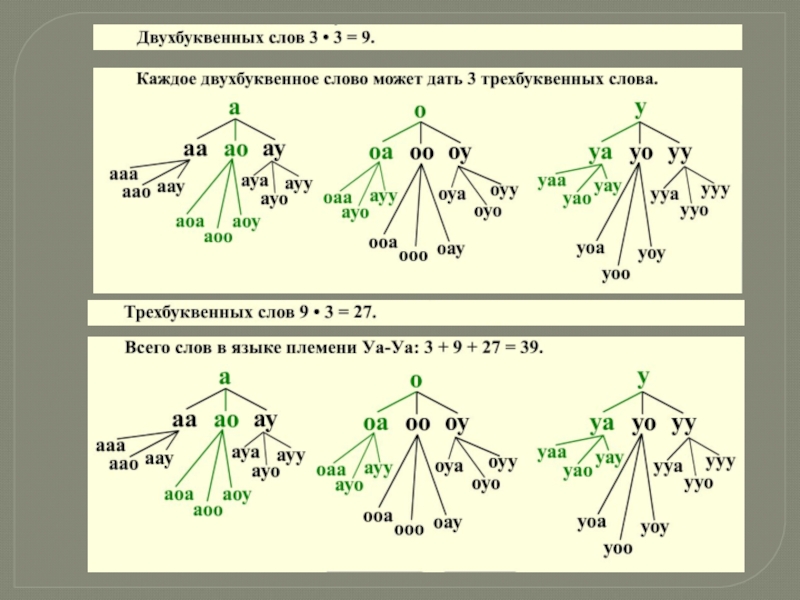
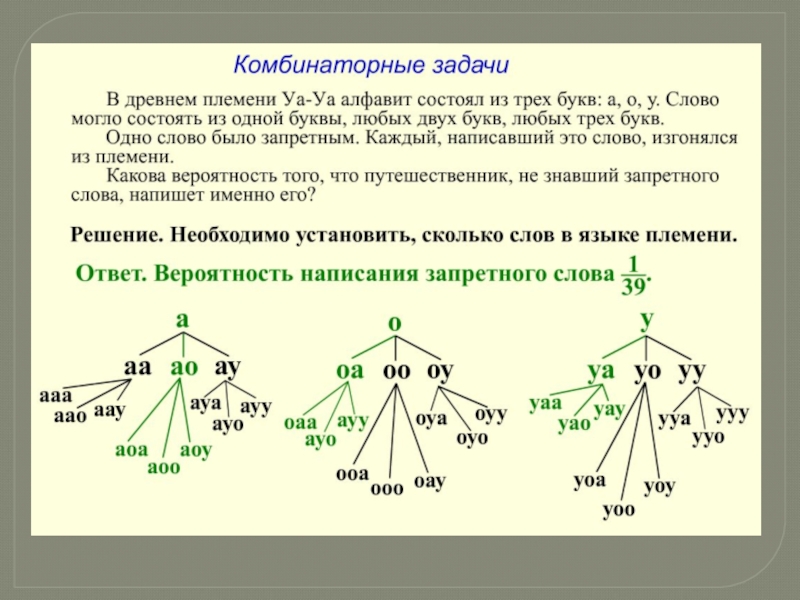
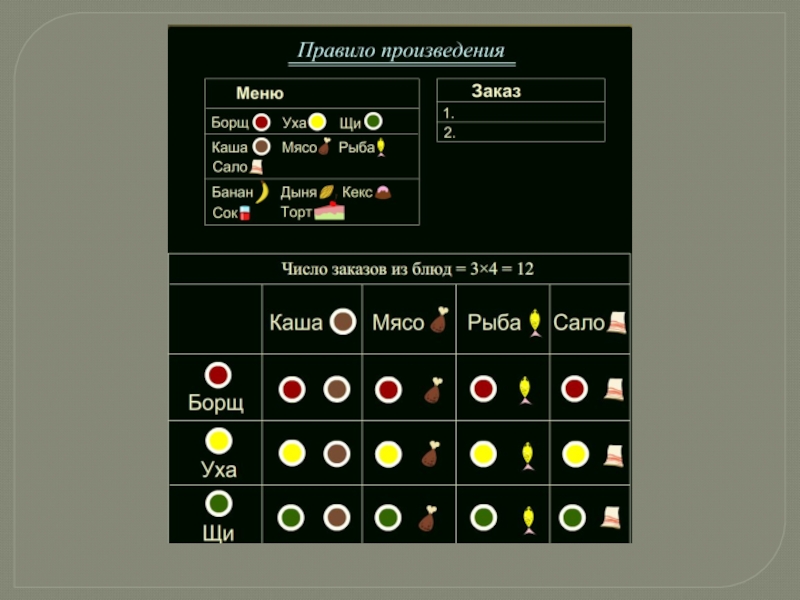
- 6. Комбинаторные задачиПростейшие комбинаторные задачи несколько напоминают игру
- 7. Слайд 7
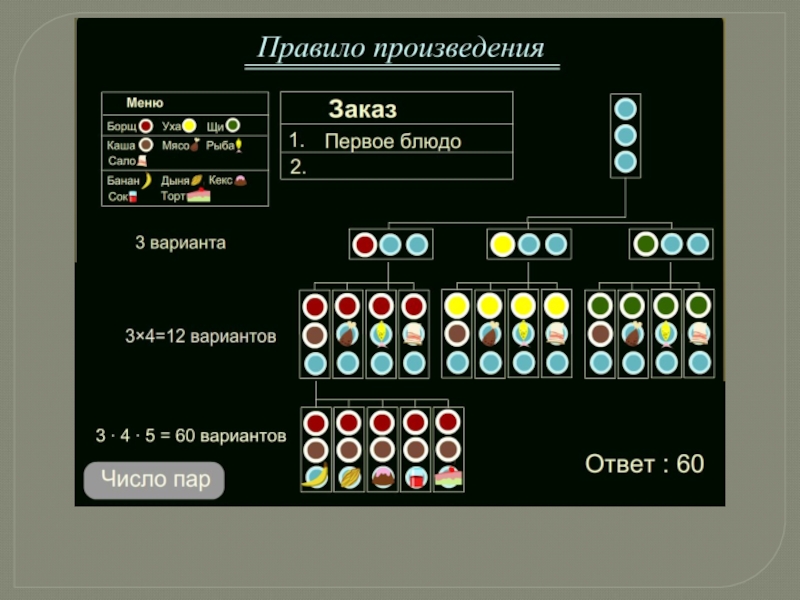
- 8. Слайд 8
- 9. Слайд 9
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
Слайд 1Комбинаторика
"Число, положение и комбинация - три взаимно пересекающиеся, но различные сферы
Иордан Ирина Ивановна
МБОУ СОШ №50
Новосибирск-2015
Слайд 2Определение
Комбинаторика - это раздел математики, в котором изучаются вопросы о том,
Слайд 3Из истории комбинаторики
Комбинаторика занимается различного вида соединениями, которые можно образовать из
Как научная дисциплина комбинаторика сформировалась в XVII в. В книге «Теория и практика арифметики» (1656 г.) французский автор А. Также посвящает сочетаниям и перестановкам целую главу.
Б. Паскаль в «Трактате об арифметическом треугольнике» и в «Трактате о числовых порядках» (1665 г.) изложил учение о биномиальных коэффициентах. П. Ферма знал о связях математических квадратов и фигурных чисел с теорией соединений. Термин «комбинаторика» стал употребляться после опубликования Лейбницем в 1665 г. работы «Рассуждение о комбинаторном искусстве», в которой впервые дано научное обоснование теории сочетаний и перестановок. Изучением размещений впервые занимался Я. Бернулли во второй части своей книги «Ars conjectandi» (искусство предугадывания) в 1713 г. современная символика сочетаний была предложена разными авторами ученых руководств только в XIX в.
Слайд 4Комбинаторика располагает столь многообразными методами, решает столь разнообразные задачи, что трудно
Слайд 5Комбинаторика — важный раздел математики, знание которого необходимо представителям самых разных
Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, и имеет широкий спектр применения, например в информатике и статистической физике.
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1665 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».