- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Квадратные уравнения
Содержание
- 1. Презентация по математике на тему Квадратные уравнения
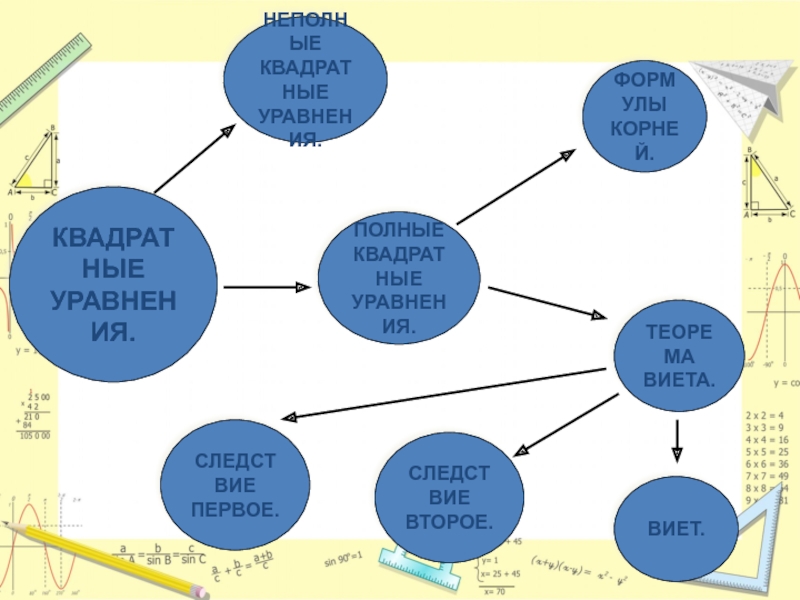
- 2. КВАДРАТНЫЕУРАВНЕНИЯ.НЕПОЛНЫЕКВАДРАТНЫЕУРАВНЕНИЯ.ПОЛНЫЕКВАДРАТНЫЕУРАВНЕНИЯ.СЛЕДСТВИЕПЕРВОЕ.СЛЕДСТВИЕВТОРОЕ.ТЕОРЕМАВИЕТА.ФОРМУЛЫКОРНЕЙ.ВИЕТ.
- 3. НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ.
- 4. ax2 + bx =
- 5. Решить уравнение 3х2 + 18х =
- 6. ax2
- 7. Решить уравнения
- 8. x2
- 9. Решите уравнение
- 10. Решите уравнение
- 11. Слайд 11
- 12. ax2 + bx + c = 0D
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Решите уравнение
- 18. Решите уравнение
- 19. следствие 1 ax2 +
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Решите уравнение –17х2 +22х+39=0.
- 24. Решите уравнение
- 25. Франсуа Виет Выполнила:Котенёва Анна Ученица 81 группы РКЛ
- 26. Франсуа Виет –выдающийся французский математик
- 27. Франсуа Виет родился
- 28. Благодаря связям матери и браку
- 29. Виет чётко представлял себе конечную цель
- 30. знаменитые «формулы Виета» для коэффициентов многочлена как
- 31. полное аналитическое изложение теории уравнений первых четырёх
- 32. Новая система мате- матического языка позволила
Слайд 2КВАДРАТНЫЕ
УРАВНЕНИЯ.
НЕПОЛНЫЕ
КВАДРАТНЫЕ
УРАВНЕНИЯ.
ПОЛНЫЕ
КВАДРАТНЫЕ
УРАВНЕНИЯ.
СЛЕДСТВИЕ
ПЕРВОЕ.
СЛЕДСТВИЕ
ВТОРОЕ.
ТЕОРЕМА
ВИЕТА.
ФОРМУЛЫ
КОРНЕЙ.
ВИЕТ.
Слайд 5Решить уравнение 3х2 + 18х = 0. Решение. 3х2 + 18х =
Слайд 7 Решить уравнения а) 2х2 – 10 =
На главную
Слайд 10 Решите уравнение
х2
Решение.
x1 + x2 = – (–4), 7 + ( – 3) = 4
x1x2 = –21, 7·( – 3) = –21
Ответ: –3; 7.
На главную
Слайд 14 Решите уравнение
Решение.
a = 3, b = 7, c = 15.
D = 72 – = –131,
Т. к. D < 0, то корней нет.
Ответ: корней нет.
Слайд 16 Решите уравнение
Решение.
a = 4, b = – 12, c = 9.
D = (– 12)2 – = 0,
Т.к. D = 0, то х = = 1,5
Ответ: 1,5.
Слайд 18 Решите уравнение
Решение.
a = 12, b = 7, c = 1.
D = 72 – = 1,
Т. к. D > 0, то х = ,
х1 = – , х2 = – .
Ответ: – ; – .
На главную
Слайд 21 Решите уравнение
Решение.
Т.к. 53 + 16 + (–69) = 0, то
по следствию 1 х1 = 1, х2= – .
Ответ: 1; – .
На главную
Слайд 24 Решите уравнение
–17х2 +22х+39=0.
Т. к. –17+39=22,
то по следствию 2 х1= –1, х2= .
Ответ: –1; .
На главную
Слайд 26 Франсуа Виет –выдающийся французский математик XVI века, положивший начало
Ф р а н с у а В и е т
Слайд 27
Франсуа Виет родился в 1540 году
Отец Виета был юристом, а мать (Маргарита Дюпон) происходила из знатной семьи, что облегчило дальнейшую карьеру её сына. Учился сначала в местном францисканском монастыре, а затем — в университете Пуатье, где получил степень бакалавра. С 19 лет занимался адвокатской практикой в родном городе.
Около 1570 года подготовил «Математический Канон» — труд по тригонометрии, — который издал в Париже в 1579 году.
В 1571 году переехал в Париж и вскоре перешёл на государственную службу, но увлечение его математикой продолжало расти.
Биография
Слайд 28 Благодаря связям матери и браку своей ученицы с принцем
Когда в результате придворных интриг Виет был на несколько лет устранён от дел, он полностью посвятил себя математике. Изучил труды классиков. Итогом его размышлений стали несколько трудов, в которых Виет предложил новый язык «общей арифметики» — символический язык алгебры.
Слайд 29 Виет чётко представлял
себе конечную цель —
разработку нового языка,
своего рода обобщённой
арифметики, которая даст
возможность проводить
математические
исследования с
недостижимыми ранее
глубиной и общностью.
Научная деятельность
Слайд 30знаменитые «формулы Виета» для коэффициентов многочлена как функций его корней;
новый тригонометрический
первый пример бесконечного произведения.
Другие заслуги Виета
Слайд 31полное аналитическое изложение теории уравнений первых четырёх степеней;
идея применения трансцендентных функций
оригинальный метод приближённого решения алгебраических уравнений с числовыми коэффициентами.
Слайд 32 Новая система мате-
матического языка
позволила просто,
ясно
описать общие законы
арифметики и алгоритмы.
Символика Виета
была сразу же оценена
учёными разных стран,
которые приступили к
её совершенствованию.
На главную