- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Динамические модели на уроках математики
Содержание
- 1. Презентация по математике Динамические модели на уроках математики
- 2. СодержаниеАктуальность вопросаИсследования ученыхПримеры динамических моделейЗначение методаЛитература по данному вопросуПриложение
- 3. Актуальность вопросаВажнейшими проблемами образования, в частности –
- 4. Л.М. Фридман о моделировании как о содержательном
- 5. Примеры динамических моделейПод динамизацией понимается, прежде всего,
- 6. При решении задач на
- 7. Значение методаДинамическое моделирование выводит учебный процесс за
- 8. ЛитератураШтоф В.А. «Моделирование и философия», Наука, 1966Фридман
- 9. 5 класс. Тема «Формулы. Площадь фигур»Карточка с
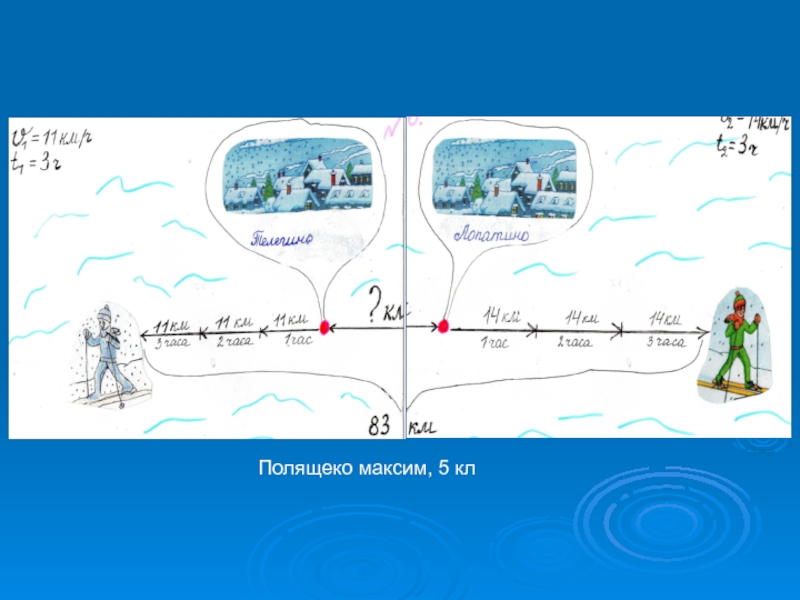
- 10. Работы учащихся 5 класс. Тема «Задачи на
- 11. Полященко Максим5 класс
- 12. Слайд 12
- 13. Слайд 13
СодержаниеАктуальность вопросаИсследования ученыхПримеры динамических моделейЗначение методаЛитература по данному вопросуПриложение
Слайд 1Динамические модели
на уроках математики
МКОУ СОШ с. Сластуха
Кондратчева О.В.
учитель математики
Слайд 2Содержание
Актуальность вопроса
Исследования ученых
Примеры динамических моделей
Значение метода
Литература по данному вопросу
Приложение
Слайд 3Актуальность вопроса
Важнейшими проблемами образования, в частности – математического, являются проблемы заинтересованности
учащегося в изучении того или
иного материала и возможности его эффективного усвоения.
Если степень заинтересованности определяется в первую очередь общекультурным уровнем учащегося , качеством и глубиной его ценностных установок (которые зависят, прежде всего, от родителей, затем от следующих уровней окружения: товарищей, СМИ, школы) и лишь во вторую очередь – трудностями усвоения учебного материала, то сама проблема усвоения связана с методикой работы с изучаемым материалом.
Методические исследования, позволяющие рассматривать возможность динамизации математических объектов как одного из средств формирования активной умственной деятельностиучащихся отражены в работах Л.М. Фридмана, И.М. Яглома, А.В. Василевского и других.
иного материала и возможности его эффективного усвоения.
Если степень заинтересованности определяется в первую очередь общекультурным уровнем учащегося , качеством и глубиной его ценностных установок (которые зависят, прежде всего, от родителей, затем от следующих уровней окружения: товарищей, СМИ, школы) и лишь во вторую очередь – трудностями усвоения учебного материала, то сама проблема усвоения связана с методикой работы с изучаемым материалом.
Методические исследования, позволяющие рассматривать возможность динамизации математических объектов как одного из средств формирования активной умственной деятельностиучащихся отражены в работах Л.М. Фридмана, И.М. Яглома, А.В. Василевского и других.
Слайд 4Л.М. Фридман о моделировании как о содержательном элементе образования пишет: «модельный
характер изучаемых понятий представляет педагогическую проекцию изучаемых наук, а вся наука есть система развивающихся знаний об определенной области или стороне действительности…процесс моделирования стал одним из основных методов научного исследования,…обладает огромной эвристической силой, позволяет свести изучение сложного к простому, неосознанное и неосязаемое к осознанному и осязаемому…Как показывают эксперименты, явное введение в содержание образования понятий модели в научном познании существенно меняет отношение учащихся к самому учебному процессу, делает их деятельность более осмысленной и продуктивной…Исследования показали также возможность овладения методом моделирования учащихся младшего школьного возраста»
А.Н. Хинчин в связи с привычной практикой получения формальных математических знаний, игнорирующей «модельный подход» писал: «Не менее тяжким следствием формализма математических знаний мы должны, наконец, признать почти полную мертвенность, бесполезность такого рода знаний в формировании научного мышления»
А.Н. Хинчин в связи с привычной практикой получения формальных математических знаний, игнорирующей «модельный подход» писал: «Не менее тяжким следствием формализма математических знаний мы должны, наконец, признать почти полную мертвенность, бесполезность такого рода знаний в формировании научного мышления»
Слайд 5Примеры динамических моделей
Под динамизацией понимается, прежде всего, процесс исследования математических объектов
и их структур с помощью изменения базисных элементов или определяющих их параметров.
Например, достаточная степень подвижности модели трапеции
позволяет выяснить, при каких условиях трапеция исчезает, вырождаясь в параллелограмм или в иной четырехугольник, при каких условиях этот четырехугольник становится трапецией.
Динамика параллелограмма, осуществляясь на подвижных моделях, позволяет получить прямоугольник, квадрат и т.п.
Динамические опорные сигналы. При изучении ФСУ. Формула квадрата суммы. Ученик постукивает два раза по первому слагаемому(символ произведения двух сомножителей), два раза по второму, по одному разу на каждом слагаемом и на двойке. Можно очень быстро проверить весь класс на владение этой моделью, после чего начинается её реализация.
Например, достаточная степень подвижности модели трапеции
позволяет выяснить, при каких условиях трапеция исчезает, вырождаясь в параллелограмм или в иной четырехугольник, при каких условиях этот четырехугольник становится трапецией.
Динамика параллелограмма, осуществляясь на подвижных моделях, позволяет получить прямоугольник, квадрат и т.п.
Динамические опорные сигналы. При изучении ФСУ. Формула квадрата суммы. Ученик постукивает два раза по первому слагаемому(символ произведения двух сомножителей), два раза по второму, по одному разу на каждом слагаемом и на двойке. Можно очень быстро проверить весь класс на владение этой моделью, после чего начинается её реализация.
Слайд 6 При решении задач на движение и работу приходится
использовать целый набор разноуровневых моделей:
исходную вербальную
гомотетичную реальную(проигрывает реальной физической ситуации в сжатом времени и пространстве)
графическую
символическую(алгебраическую)
Динамическое моделирование открывает возможности для математического эксперимента. Например, процесс наблюдения за изменением положения вершины треугольника при фиксированном основании. Объектами наблюдения здесь являются медиана, биссектриса, высота, проведенная к основанию и его серединный перпендикуляр. Наблюдаемые явления: совпадение линий, расположенность «между», изменение углов.
Моделирование может носить глобальный характер: моделирование логических форм, доказательств, методов решения задач, методологии исследования, алгоритмов, высказываний и даже понятий. Например, при изучении углов, образованных при пересечении двух прямых третьей, вводятся буквенные модели, которые позволяют зрительно находить углы на чертежах: внутренние накрест лежащие –Z углы, соответственные F- углы, внутренние односторонние П – углы. При обозначении признаков равенства треугольников можно по примеру некоторых американских учебников вводить СУС, ССС, УСУ.
исходную вербальную
гомотетичную реальную(проигрывает реальной физической ситуации в сжатом времени и пространстве)
графическую
символическую(алгебраическую)
Динамическое моделирование открывает возможности для математического эксперимента. Например, процесс наблюдения за изменением положения вершины треугольника при фиксированном основании. Объектами наблюдения здесь являются медиана, биссектриса, высота, проведенная к основанию и его серединный перпендикуляр. Наблюдаемые явления: совпадение линий, расположенность «между», изменение углов.
Моделирование может носить глобальный характер: моделирование логических форм, доказательств, методов решения задач, методологии исследования, алгоритмов, высказываний и даже понятий. Например, при изучении углов, образованных при пересечении двух прямых третьей, вводятся буквенные модели, которые позволяют зрительно находить углы на чертежах: внутренние накрест лежащие –Z углы, соответственные F- углы, внутренние односторонние П – углы. При обозначении признаков равенства треугольников можно по примеру некоторых американских учебников вводить СУС, ССС, УСУ.
Слайд 7Значение метода
Динамическое моделирование выводит учебный процесс за пределы собственно математики, на
более широкое поле деятельности: в область логики, семантики, гносеологии, методологии науки, а количество используемых моделей отнюдь не обременяет учебный процесс, а делает его более интересным, насыщенным и, в то же время, методологически прозрачным. Осознается системный и многомодельный подходы к изучению реального мира, осознается всё богатство его взаимосвязей, происходит синтез различных областей познания. Поскольку все науки (не только математика) используют различные эвристические, объяснительные, интерпретирующие, предсказательные теоретические модели, изучают взаимозависимость различных явлений своей области познания, то динамическое моделирование является общим методом всех наук, специфически проявляясь в каждой из них.
Введение в школьное образование этого метода давно назрело и, в конечном счете, - неизбежно, обо нельзя до бесконечности игнорировать основной метод познания действительности.
Введение в школьное образование этого метода давно назрело и, в конечном счете, - неизбежно, обо нельзя до бесконечности игнорировать основной метод познания действительности.
Слайд 8Литература
Штоф В.А. «Моделирование и философия», Наука, 1966
Фридман Л.М. «Психолого-педагогические основы обучения
математике в школе»
Василевский А.В. «Сборник динамических задач и упражнений по геометрии», Минск, 1997
Василевский А.В. «Упражнения по алгебре и началам анализа», Минск, 1997
Фройденталь Г. «Математика как педагогическая задача», Просвещение,1983
Зиновьев А.А. «Логика науки», Мысль,1971
Василевский А.В. «Сборник динамических задач и упражнений по геометрии», Минск, 1997
Василевский А.В. «Упражнения по алгебре и началам анализа», Минск, 1997
Фройденталь Г. «Математика как педагогическая задача», Просвещение,1983
Зиновьев А.А. «Логика науки», Мысль,1971
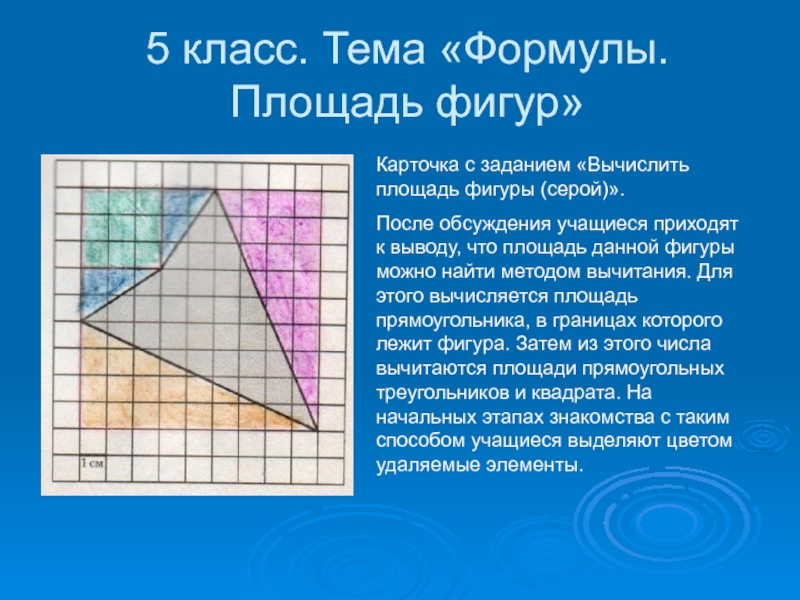
Слайд 95 класс. Тема «Формулы. Площадь фигур»
Карточка с заданием «Вычислить площадь фигуры
(серой)».
После обсуждения учащиеся приходят к выводу, что площадь данной фигуры можно найти методом вычитания. Для этого вычисляется площадь прямоугольника, в границах которого лежит фигура. Затем из этого числа вычитаются площади прямоугольных треугольников и квадрата. На начальных этапах знакомства с таким способом учащиеся выделяют цветом удаляемые элементы.
После обсуждения учащиеся приходят к выводу, что площадь данной фигуры можно найти методом вычитания. Для этого вычисляется площадь прямоугольника, в границах которого лежит фигура. Затем из этого числа вычитаются площади прямоугольных треугольников и квадрата. На начальных этапах знакомства с таким способом учащиеся выделяют цветом удаляемые элементы.