- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему: Пирамида
Содержание
- 1. Презентация по геометрии на тему: Пирамида
- 2. Египетские пирамиды – одно из семи чудес
- 3. Пирамидой называется многогранник, который состоит из плоского
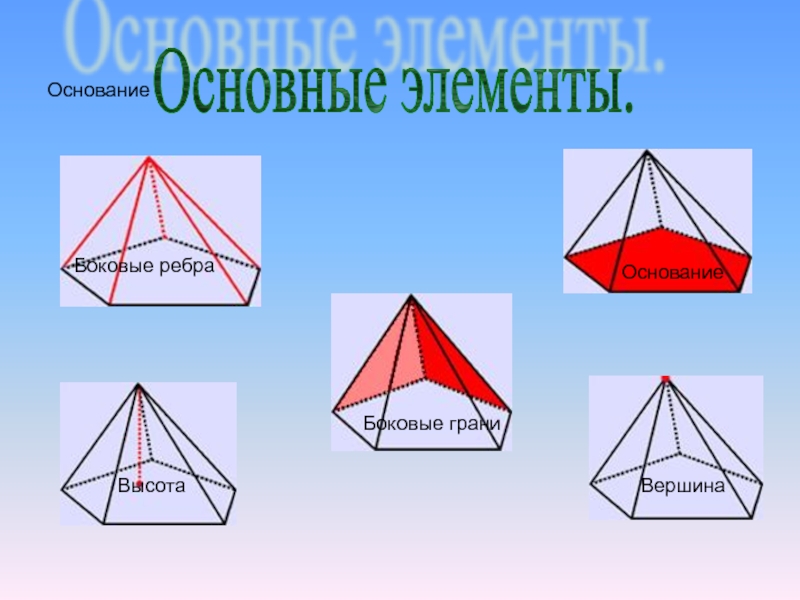
- 4. ОснованиеОснование ВысотаБоковые граниВершинаБоковые ребраОсновные элементы.
- 5. Сечения пирамиды плоскостями, проходящими через ее вершину,
- 6. Виды пирамидПравильнаяУсеченная
- 7. Пирамида называется правильной, если ее основание- правильный
- 8. Если две правильные четырехугольные пирамиды, у которых
- 9. Теорема: Площадью боковой поверхности правильной пирамиды равна
- 10. Sбок = 0.5РhТеорема: Боковая поверхность правильной пирамиды
- 11. Объем любой пирамиды равен одной трети произведения
- 12. Плоскость, параллельная плоскости основания пирамиды и пересекающая
- 13. Усеченная пирамида называется правильной, если она составляет
- 14. Теорема: Площадь боковой поверхности правильной усеченной пирамиды
- 15. Слайд 15
- 16. 1. Одно из самых грандиозных сооружений древности
- 17. 2. Дано: SABCD – Правильная четырехугольная пирамида.
- 18. 1. Лаппо Л.Д. Геометрия: Устный экзамен. Теория
- 19. №1 В основании пирамиды лежит прямоугольный треугольник,
- 20. №4 В правильной четырехугольной пирамиде сторона основания
- 21. №7 В правильной четырехугольной пирамиде сторона основания
- 22. Пройти следующий тест.(1,2,3)
- 23. Попробовать еще раз.Ты был не внимателен !Попробуй еще!Попробовать еще раз.Не верно
- 24. Ты усвоил эту тему!ВерноПройти следующий тест(4,5,6)Пройти следующий тест(7,8,9)
- 25. Ты был не внимателен !Попробуй еще!Не верноПопробовать еще раз!
- 26. Слайд 26
- 27. Ты был не внимателен !Попробуй еще!Не верноПопробовать еще раз
Слайд 2
Египетские пирамиды – одно из семи чудес света.… Как загадочны эти
Пирамиды, несмотря на свою древность, могут многому нас научить. Исследованием пирамид с использованием новейших приборов занимались американцы, японцы. Пирамиды снимали со спутников. Американская станция "Маринер"' передала фотографии с Марса, на которых изображены такие же пирамиды, что наводит на мысль об их внеземном происхождении. Так что же такое пирамиды?
Введение.
Слайд 3
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды,
Отрезки, соединяющие вершину пирамиды с вершинами основания называются боковыми ребрами.
Пирамида может быть получена при пересечении многогранного угла произвольной плоскостью. Ее вершиной будет служить вершина многогранного угла, основанием – сечение многогранного угла данной плоскостью, боковыми ребрами – отсеченные части ребер многогранного угла.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Площадью полной поверхности пирамиды называется сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.
"Пирамида"
Слайд 5
Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники .
Плоскость, проведенная через вершину пирамиды и через какую-нибудь диагональ основания, называется диагональной плоскостью.
∆SEF – сечение пирамиды SABCD
∆SDB – диагональное сечение пирамиды SABCD
Диагональные сечения пирамиды
Слайд 7
Пирамида называется правильной, если ее основание- правильный многоугольник, а отрезок, соединяющий
Следовательно, все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. Высота каждая из этих треугольников называется апофемой. Все апофемы правильной пирамиды равны. Боковые ребра и боковые грани правильной пирамиды имеют один и тот же угол наклона к плоскости основания.
"Правильная пирамида"
Слайд 8
Если две правильные четырехугольные пирамиды, у которых боковое ребро равно стороне
Четыре атома водорода , входящие в молекулы метана, расположены в вершинах правильной пирамиды (тетраэдра). Атом углерода находится внутри этой пирамиды на равном расстоянии от ее вершин.
Примеры "Правильной пирамиды"
Слайд 9
Теорема: Площадью боковой поверхности правильной пирамиды равна половине произведения периметра основания
Дано :правильная пирамида.
Доказать,что S боковой
поверхности равна 1\2
P основания на апофему.
Решение.
Боковые грани правильной пирамиды-равные равнобедренные треугольники , основания которых-стороны основания пирамиды, а высоты равны апофеме.S боковой поверхности пирамиды равна сумме произведений сторон основания на половину апофемы а .Вынося множитель 1\2 а за скобки, получим в скобках сумму сторон основания пирамиды ,т.е. его периметр .Ч.т.д.
Доказательство теоремы
Слайд 10Sбок = 0.5Рh
Теорема: Боковая поверхность правильной пирамиды равна произведению полупериметра основания
Где P-периметр основания пирамиды, а
h-апофема
Теорема: Площадь полной поверхности пирамиды (рис.9а) вычисляется по формуле:
Sполн = Sбок + Sосн
Площадь пирамиды
Sбок = 0.5Рh
а
б
Слайд 11
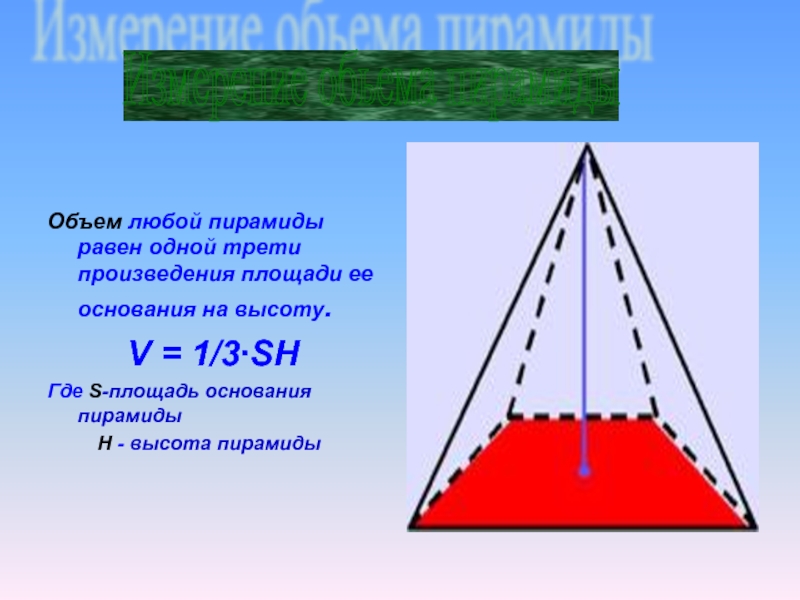
Объем любой пирамиды равен одной трети произведения площади ее основания на
V = 1/3∙SH
Где S-площадь основания пирамиды
H - высота пирамиды
Измерение обьема пирамиды
Слайд 12
Плоскость, параллельная плоскости основания пирамиды и пересекающая ее боковые ребра, отсекает
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-нибудь точки одного основания на плоскость другого основания. Сечение плоскостью, проходящей через два боковых ребра усеченной пирамиды, не лежащих в одной грани, называется диагональным.
Чтобы построить усеченную пирамиду, сначала намечают карандашом полную пирамиду, проводят сечение, параллельное основанию, проводят ребра усеченной пирамиды, а верхнюю часть стирают.
Усечённая пирамида
Слайд 13
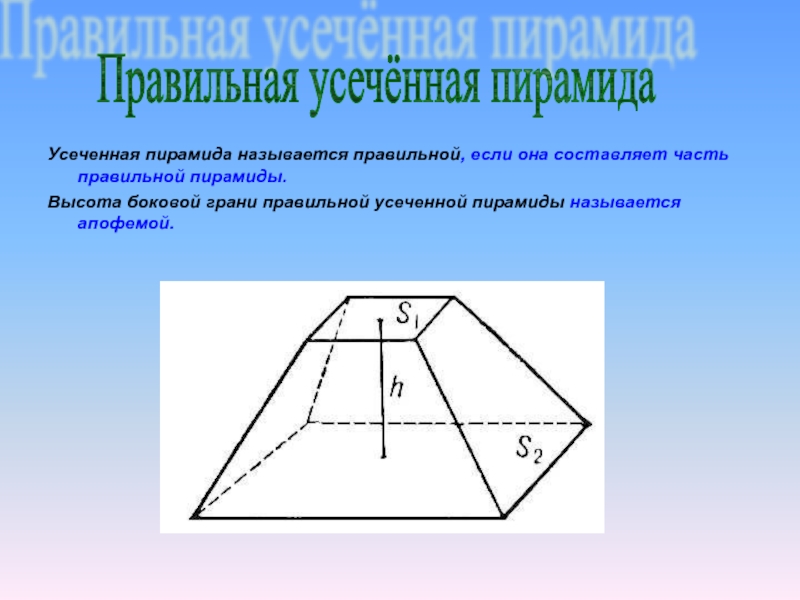
Усеченная пирамида называется правильной, если она составляет часть правильной пирамиды.
Высота боковой
Правильная усечённая пирамида
Слайд 14
Теорема: Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров
Дано: n-угольная правильная усеченная пирамида,
l – апофема, P и P1 – периметры оснований.
Доказать: Sбок = ½(p+p1) ∙l
Решение.
В правильной усеченной пирамиде все боковые грани – равные между собой трапеции. Пусть основания трапеции a и a1, ее высота k, тогда Sгр. = ½(a + a1)∙l, таких граней n,
следовательно, Sбок = n ½ (a + a1) l = ½ (na + na1)∙l, т.е. Sбок = ½ (P+P1)∙l. Ч.т.д.
Площадь боковой и полной поверхности усечённой пирамиды
Слайд 15
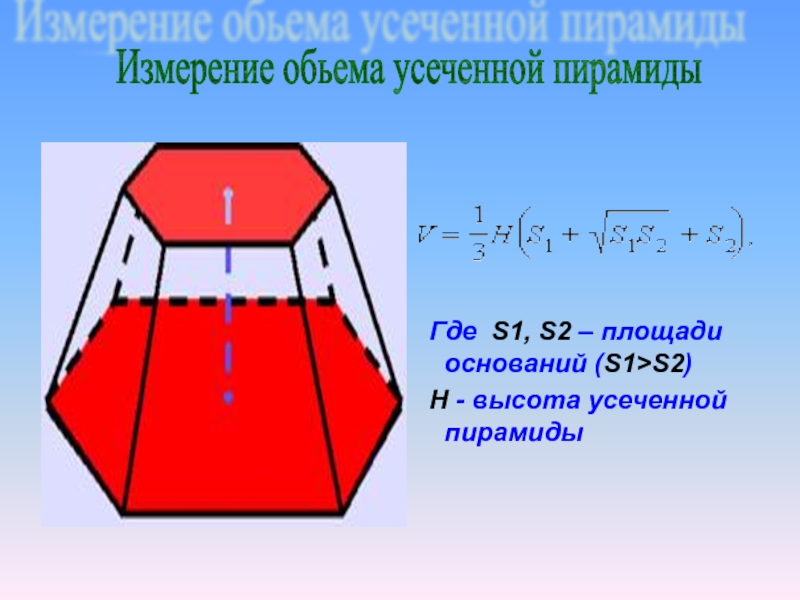
Где S1, S2 – площади оснований (S1>S2)
H - высота усеченной пирамиды
Измерение обьема усеченной пирамиды
Слайд 16
1. Одно из самых грандиозных сооружений древности – пирамида Хеопса –
2. Крыша имеет форму пирамиды с квадратным основанием 4,5 м × 4,5 м и углом наклона грани к основанию в 45˚. Сколько листов железа размером 70 см × 140 см нужно для покрытия крыши, если на отходы нужно добавить 10% площади крыши?
Задачи
Слайд 17
2. Дано: SABCD – Правильная четырехугольная пирамида. AB = BC =
Найти: N
Решение:
N = (Sбок + S отх )/ S листа
Sбок = 4∙S∆CSD =4 ½ CD∙SK = 2CD∙SK
Рассмотрим. ∆SOC (O = 90˚; С = 45˚)
т.к. сумма углов в треугольнике равна 180˚,то S = 180˚ – 90˚ – 45˚ = 45˚ → SO = OC
т.к. ABCD – правильный четырехугольник, то OK = CD/2 = 4,5/2 = 2, 25 (м)
Рассмотрим. ∆OKC (K = 90˚; OK = CK)
По теореме Пифагора: OC = √2OK2 = √2∙5, 0625 ≈ 3, 2 (м) → SO = 3, 2 (м)
Рассмотрим. ∆SOK (O = 90˚)
По теореме Пифагора: SK = √SO2 + OK2 = √10, 24 + 5, 0625 = √15, 3 ≈ 3, 9 (м)
Sбок = 2∙4, 5∙3, 9 = 35, 1 (м2)
S отх = Sбок∙0, 1 = 35, 1∙0, 1 = 3, 51 (м2)
S листа = 0, 7∙1, 4 = 0, 98 (м2)
N = (35, 1 + 3, 51)/0, 98 = 40
Ответ: 40 листов
1. Дано: SABCD – правильная четырехугольная пирамида; SO – высота; SO = 150 м; SA – боковое ребро; SA = 220 м;
Найти: VSABCD; Sбок
Решение:
V = 1/3SABCDSO; Sбок = p∙SK/2
Рассмотрим. ∆SOC (O = 90˚)
По теореме Пифагора: OC = √SC2 – SO2 = √2202 – 1502 = √48400 – 22500 = √25900 (м) ≈ 161 м
т.к. ABCD – правильный прямоугольник, то: AB = OC√2 = √25900*2 = √51800 (м) ≈ 228 (м)
Рассмотрим. ∆ SCD (SC = CD = SD)
CK= ½ CD; CK = 228/2 = 114 (м)
Рассмотрим. ∆SKC (K = 90˚)
По теореме Пифагора: SK = √SC2 – CK2; SK = √2202 – 1142 = √48400 – 12996 = √35404 ≈ 188 (м)
Периметр основания: p = 4∙228 = 912 (м)
Находим Sбок = 4∙228∙114/2 = 51984 (м2)
Sосн = AB2; Sосн = 2282 = 51984 (м2)
Находим V= 1/3SABCDSO = 1/3∙51984∙150 = 2599200 (м3)
Ответ: 51984 м2; 2599200 м3.
Решение задач
Слайд 18
1. Лаппо Л.Д. Геометрия: Устный экзамен. Теория и практика. Издательство «ЭКЗАМЕН»,2008.
2.
3. Погорелов А.В. Геометрия: Учебник для 7-11, 5-е изд. М: Просвещение, 1996.
4. Савин А.П. Энциклопедический словарь юного математика. М.: Просвещение, 1985.
5. Шарыгин И.Ф. Факультативный курс по математике. XI класс. М.: Просвещение, 1991.
6. Атанасян Л.С. Геометрия: Учебник для 10-11, 16-е изд.М: Просвещение,1992.
Список использованной литературы
Слайд 19
№1 В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 15
13,5см² 27 см² 108 см²
№2 В правильной четырехугольной пирамиде высота равна 12, а апофема -15 см.Найдите боковое ребро пирамиды.
3 √ 34 см 34 см 12см 34 см 12см 9 √ 34
№3 В правильной четырехугольной пирамиде высота равна стороне основания. Найдите угол между боковым ребром и плоскостью основания.
60˚ 30 ˚ 15 ˚
тест
Слайд 20№4 В правильной четырехугольной пирамиде сторона основания равна 12 см, а
3 √ 21см 21см 3√ 21см² 3 √ 29см
№5 Найдите боковую поверхность правильной четырехугольной пирамиды, у которой диагональное сечение равновелико основанию , если стороны основа В правильной четырехугольной пирамиде стороны основания равна а 3а ² 3а√ 3 3 4а √ ½
№6 Найдите боковую поверхность пирамиды ,если площадь основания равна S,а двугранные углы при основании равны а.
SсмSсм S\cosα см см cosα см
тест
Слайд 21№7 В правильной четырехугольной пирамиде сторона основания равна 10 см, а
360см² 230см ² 140 см ²
№8 Основанием пирамиды является равнобедренная трапеция с основаниями 6 см и 4 √ 6 см и высотой 5 см.Каждое боковое ребро пирамиды равно 13 см.Найдите ее высоту.
12 см ≈13см ≈13см 5,2см
№9 Основанием пирамиды, высота которой равна 2 дм, а боковые ребра равны друг другу, является прямоугольник со сторонами 6 дм и 8 дм. Найдите площадь сечения, проведенного через диагональ основания параллельно боковому ребру.
13 дм ² 13 дм 13 дм 26 дм ²
тест
Слайд 22Пройти следующий тест.(1,2,3)
Пройти следующий тест.(1,2,3)
Верно
Пройти следующий тест.(4,5,6)